nLab HaPPY code

Idea

The hyperbolic pentagon code or HaPPY code is a quantum error correction code (a class of such codes really, indexed by a “cutoff” natural number) which is thought to exhibit characteristic properties akin to the encoding of bulk-quantum states by boundary-states expected in the AdS/CFT correspondence. In particular, the HaPPY code (or rather the tensor network that defines it) exhibits a discretized form of the Ryu-Takayanagi formula for holographic entanglement entropy.

Concretely, the the HaPPY code subspace is the image of the linear map formed by:

From Harlow 18

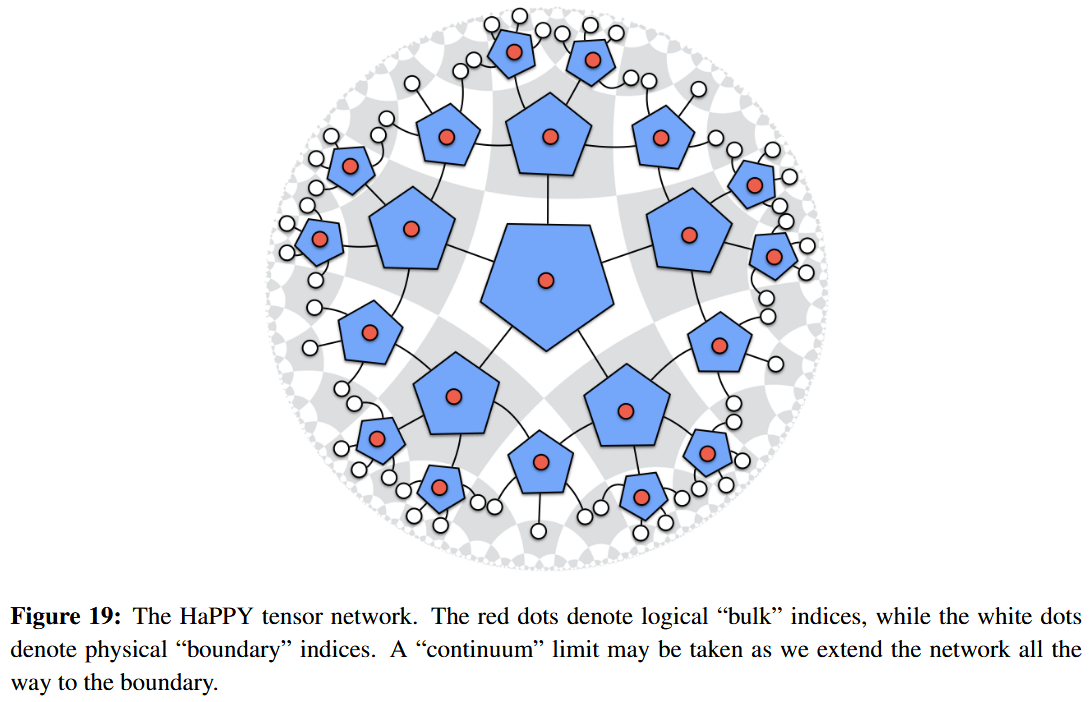
1. picking a perfect tensor $T$ of rank 6;

2. picking a finite cutoff of the pentagonal tesselation $\{5,4\}$ of the hyperbolic plane;

3. regarding its Poincaré dual graph as a tensor network (string diagram in finite-dimensional vector spaces) by

   1. assigning $T$ to each vertex at the center of the pentagons (show in blue), with 5 of its indices contracted with its neighbours in the hyperbolic plane,

   2. and its 6th uncontracted index remaining as an input (shown in red);

   3. regading the uncontrated edges at the cutoff boundary as output (shown in white)

and thus as a linear map form the tensor product over the bulk-vertices to the tensor product over the edges sticking out over the boundary.

Related concepts

• stabilizer code

• bit flip code

• Majorana dimer code

References

Tha HaPPY code is due to

• Fernando Pastawski, Beni Yoshida, Daniel Harlow, John Preskill, Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence, JHEP 06 (2015) 149 (arXiv:1503.06237)

following a precursor observation in

• Ahmed Almheiri, Xi Dong, Daniel Harlow, Bulk Locality and Quantum Error Correction in AdS/CFT, JHEP 1504:163,2015 (arXiv:1411.7041)

Review in:

• Daniel Harlow, TASI Lectures on the Emergence of Bulk Physics in AdS/CFT (arXiv:1802.01040)

See also:

• Elliott Gesteau, Monica Jinwoo Kang, The infinite-dimensional HaPPY code: entanglement wedge reconstruction and dynamics (arXiv:2005.05971)

Variation to be more truthful to AdS/CFT:

• Rafał Bistroń, Mykhailo Hontarenko, Karol Życzkowski: Bulk-boundary correspondence from hyper-invariant tensor networks [arXiv:2409.02029]