nLab matrix product state
Context
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
What are called matrix product states (MPS) in quantum physics (specifically in solid state physics and in AdS/CFT) are those tensor network states of the form of a ring of tensors all of rank 3.
For example, given a metric Lie algebra (with string diagram-notation as discussed there) its Lie bracket-tensor gives rise to matrix product states of the following form:
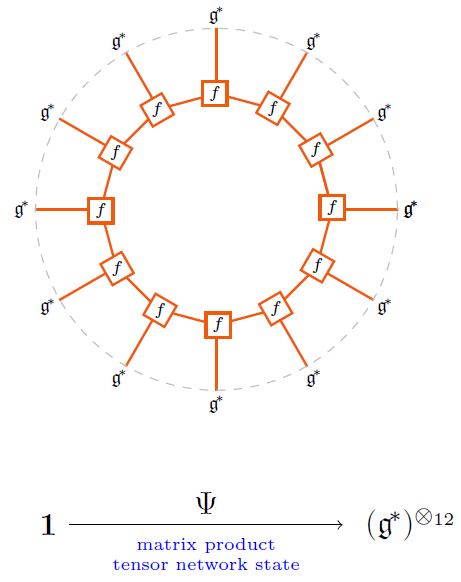
graphics from Sati-Schreiber 19c
Related concepts
References
For more see the references at tensor network state.
General
Review and exposition:
-
Roman Orus, Section 5.1 of: A Practical Introduction to Tensor Networks: Matrix Product States and Projected Entangled Pair States, Annals of Physics 349 (2014) 117-158 (arXiv:1306.2164)
-
Jens Eisert, Section 2 of: Entanglement and tensor network states, Modeling and Simulation 3, 520 (2013) (arXiv:1308.3318)
-
Jacob Biamonte, Ville Bergholm, Section 5 of: Tensor Networks in a Nutshell, Contemporary Physics (arxiv:1708.00006)
-
Bei Zeng, Xie Chen, Duan-Lu Zhou, Xiao-Gang Wen:
Sec. 8 of: Quantum Information Meets Quantum Matter – From Quantum Entanglement to Topological Phases of Many-Body Systems, Quantum Science and Technology (QST), Springer (2019) arXiv:1508.02595, doi:10.1007/978-1-4939-9084-9
-
Jacob Biamonte, Chapter II of: Lectures on Quantum Tensor Networks (arXiv:1912.10049)
-
Shi-Ju Ran, Emanuele Tirrito, Cheng Peng, Xi Chen, Luca Tagliacozzo, Gang Su, Maciej Lewenstein, Section 2.3.2 of: Tensor Network Contractions, Lecture Notes in Physics, Springer (2020) (arXiv:1708.09213, doi:10.1007/978-3-030-34489-4)
-
Roman Orus, Chapter II of: Tensor networks for complex quantum systems, Nature Reviews Physics 1, 538-550 (2019) (arXiv:1812.04011, doi:10.1038/s42254-019-0086-7)
See also:
-
Wikipedia, Matrix product state
-
Frank Verstraete, J. Ignacio Cirac, V. Murg: Matrix Product States, Projected Entangled Pair States, and variational renormalization group methods for quantum spin systems, Adv. Phys. 57 (2008) 143 [arXiv:0907.2796, doi:10.1080/14789940801912366]
In quantum computation
In the context of quantum computation:
- Yiqing Zhou, E. Miles Stoudenmire, Xavier Waintal, What limits the simulation of quantum computers? (arXiv:2002.07730)
Last revised on October 29, 2024 at 10:37:58. See the history of this page for a list of all contributions to it.