nLab Dwyer-Wilkerson H-space
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Exceptional structures
exceptional structures, exceptional isomorphisms
Examples
-
exceptional finite rotation groups:
-
and Kac-Moody groups:
-
exceptional Jordan superalgebra,
Interrelations
Applications
Philosophy
Contents
Idea
The Dwyer-Wilkerson space (Dwyer-Wilkerson 93) (also denoted ) is a 2-complete H-space, in fact a finite loop space/∞-group, such that the mod 2 cohomology ring of its classifying space/delooping is the mod 2 Dickson invariants of rank 4. As such, it is the fifth and last space (see below) in a series of ∞-groups that starts with 4 compact Lie groups, namely with the automorphism groups of real normed division algebras:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 1 | Z/2 | SO(3) | G2 | G3 | |
| = Aut(R) | = Aut(C) | = Aut(H) | = Aut(O) |
whence the notation “” (suggested in Møller 95, p. 5).
While is not a compact Lie group, it is a 2-compact group, hence a “homotopy Lie group” (see below).
The above progression starting with the automorphism groups of real normed division algebras suggests that has a geometric or algebraic relevance in a context of division algebra and supersymmetry. This remains open, but there are speculations, see below.
Properties
Cohomology
The ordinary cohomology of the classifying space/delooping with coefficients in the prime field is, as an associative algebra over the Steenrod algebra, the ring of mod 2 Dickson invariants of rank 4. This is the ring of invariants of the natural action of on the rank 4 polynomial algebra , a polynomial algebra on classes , , , and with , , and .
(Dwyer-Wilkerson 93, Theorem 1.1)
As such, is the last in a series of ∞-groups whose classifying spaces/deloopings have as mod 2 cohomology ring the mod 2 Dickson invariants for rank , which starts with three ordinary compact Lie groups:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| Z/2 | SO(3) | G2 | G3 |
(Dwyer-Wilkerson 93, top of p. 38 (2 of 28))
This means in particular that the cohomology is an exterior algebra on generators of degree 7, 11, 13, 14 so it’s (2-locally) a Poincaré duality space of dimension 45.
(…)
Construction as a homotopy colimit
The space is the 2-completion of the homotopy colimit of a diagram (Notbohm 03, Sec. 2, Ziemianski, 0.2.3).
As a 2-compact group
is the only exotic 2-group, or, in other words, the only simple 2-compact group not arising as the 2-completion of a compact connected Lie group (Andersen-Grodal 06).
Weyl group
The analog of the Weyl group for is .
(Dwyer-Wilkerson 93, middle of p. 38 (2 of 28))
Homotopy coset space
receives a homomorphism from Spin(7). The homotopy fiber of the corresponding delooping map is a homotopy-coset space
The ordinary cohomology with coefficients in the prime field of this space has Euler characteristic 7 (Notbohm 03, Remark 2.3, Aguadé 10, p. 4133), equal to the index of the respective Weyl groups. (Note this corrects an error in (Dwyer-Wilkerson 93, Theorem 1.8).)
Relation to the Conway group,
receives a map from , the delooping/classifying space of the Conway group, . This map has the property that it injects the mod two cohomology of as a subring over which the mod two cohomology of is finitely generated as a module (see Benson 94). This continues a pattern from and , where is a Mathieu group. For further developments see (Aschbacher-Chermak 10).
and both contain as 2-local subgroups the non-split extension, .
Relation to octonionic matrix algebra?
Since, by the above, is (2-locally) a Poincaré duality space of dimension 45, there has been speculation that it might be related to the -dimensional algebra
of skew-hermitian matrices over the octonions (Solomon-Stancu 08, p. 175, Wilson 09a, slide 94, Benson 98, p. 19). (Wilson’s suggestion appears to arise from his construction of a 3-dimensional octonionic Leech lattice, his representation of its automorphism group, the Conway group , as right multiplications by matrices over the octonions (Wilson 09b), and the relationship between the latter’s subgroup and .)
Incidentally, the algebra of hermitian matrices (as opposed to skew-hermitian) over the octonions
is the exceptional Jordan algebra called the Albert algebra (see there).
Homotopy representation
The possibility of there being a faithful 15-dimensional real homotopy representation of is raised in (Baker-Bauer 19, p. 8).
Related concepts
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G₂ is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G₂/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
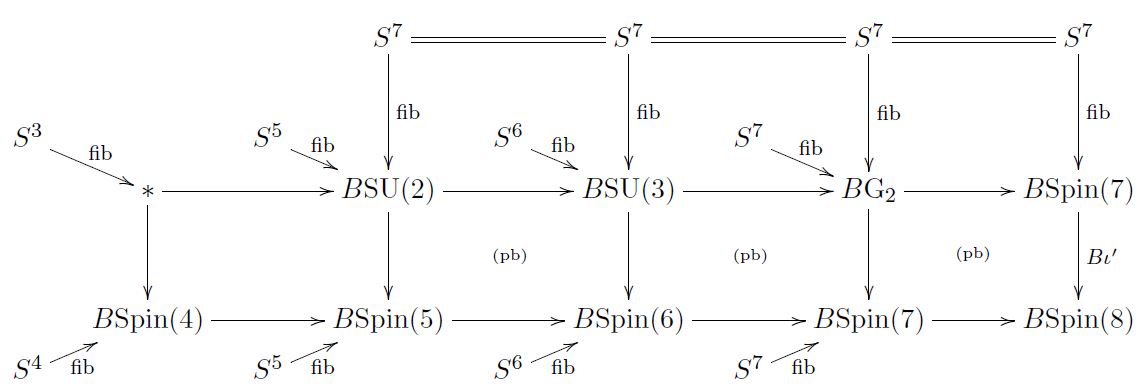
(from FSS 19, 3.4)
References
Due to
- William Dwyer, Clarence Wilkerson, A new finite loop space at the prime two, J. Amer. Math. Soc. 6 (1993), 37-64 (doi:10.1090/S0894-0347-1993-1161306-9)
Review:
-
Jesper Møller, Homotopy Lie groups, Bull. Amer. Math. Soc. (N.S.) 32 (1995) 413-428 (arXiv:math/9510218)
-
Jesper Grodal, The Classification of –Compact Groups and Homotopical Group Theory, Proceedings of the International Congress of Mathematicians, Hyderabad 2010 (arXiv:1003.4010, pdf, pdf)
-
Dietrich Notbohm, On the compact 2-group , Journal für die reine und angewandte Mathematik (Crelles Journal), Volume 2003, Issue 555, Pages 163–185, (pdf)
See also
-
David Benson, Conway’s group and the Dickson invariants, Manuscripta Math (1994) 85: 177 (dml:156016)
-
Krzysztof Ziemiański, A faithful complex representation of the 2-compact group DI(4), 2005 (thesis)
-
Kasper Andersen, Jesper Grodal, The classification of 2-compact groups, J. Amer. Math. Soc. 22 (2009), 387-436 (arXiv:math/0611437)
-
Martin Bendersky, Donald M. Davis, -periodic homotopy groups of the Dwyer-Wilkerson space (arXiv:0706.0993)
-
Michael Aschbacher, Andrew Chermak, A group-theoretic approach to a family of 2-local finite groups constructed by Levi and Oliver, Annals of Mathematics, Volume 171 (2010), Issue 2 (doi:10.4007/annals.2010.171.881,pdf)
-
Jaume Aguadé, The torsion index of a -compact group, Proceedings of the AMS, Vol. 138, No. 11, 2010 (jstor:25748300)
-
Andrew Baker, Tilman Bauer, The realizability of some finite-length modules over the Steenrod algebra by spaces (arXiv:1903.10288)
Speculation on possible geometric roles of :
-
Eon Solomon, Radu Stancu, p. 175 of: Conjectures on finite and p-local groups, L’Enseignement Mathématique (2) 54 (2008) 171-176 (pdf, doi:10.5169/seals-109929)
-
David Benson, Cohomology of Sporadic Groups, Finite Loop Spaces, and the Dickson Invariants, in P. Kropholler, G. Niblo, & R. Stöhr (Eds.), Geometry and Cohomology in Group Theory (London Mathematical Society Lecture Note Series, pp. 10-23), 1998. Cambridge University Press.
-
Robert A. Wilson, Slide 94 of: A new approach to the Leech lattice, talk at University of Cambridge, 21st October 2009 (slides pdf)
(on an octonionic construction of the Leech lattice)
-
Robert A. Wilson, Conway’s group and octonions, (pdf)
Last revised on March 30, 2025 at 12:38:16. See the history of this page for a list of all contributions to it.