nLab E₆
Context
Exceptional structures
exceptional structures, exceptional isomorphisms
Examples
-
exceptional finite rotation groups:
-
and Kac-Moody groups:
-
exceptional Jordan superalgebra,
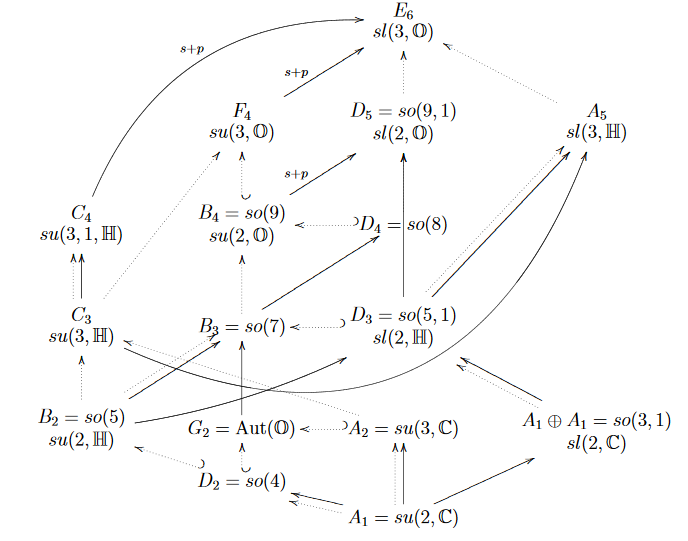
Interrelations
Applications
Philosophy
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Contents
Idea
One of the exceptional Lie groups.
Properties
As automorphisms of the exceptional Jordan algebra
The group of determinant-preserving linear isomorphisms of the vector space underlying the octonionic Albert algebra is . (see e.g. (Manogue-Dray 09)).
This may be written as . (Dray-Manogue 09a (16))
graphics grabbed from (Dray-Manogue 09a, p. 12)
Outer automorphism
The Dynkin diagram of has 2-fold symmetry, corresponding to a nontrivial outer automorphism of order 2. acts on the octonionic projective plane and its outer automorphism gives rise to a projective duality in its geometry.
As part of the ADE pattern
ADE classification and McKay correspondence
As U-duality group of 5d SuGra
is the U-duality group (see there) of 11-dimensional supergravity compactified to 5 dimensions.
Related concepts
References
-
Tevian Dray, Corinne Manogue, Octonionic Cayley spinors and (pdf)
-
Corinne Manogue, Tevian Dray, Octonions, , and Particle Physics, J.Phys.Conf.Ser.254:012005,2010 (arXiv:0911.2253)
A description of as the special linear group in dimension 3 with values in the octonions is given in
-
Corinne Manogue, Tevian Dray, Octonions and the Structure of Comment. Math. Univ. Carolin., 51:193–207, 2010.
-
Aaron Wangberg, Tevian Dray, , the Group: The structure of (arXiv:1212.3182)
Cohomological properties are discussed in
-
Mamoru Mimura, Yuriko Sambe, Michishige Tezuka, Cohomology mod 3 of the classifying space of the exceptional Lie group , I : structure of Cotor (arXiv:1112.5811),
Cohomology mod 3 of the classifying space of the exceptional Lie group , II : The Weyl group invariants (arXiv:1201.3414)
See also:
- Wikipedia, E₆
On -exceptional field theory formulation of D=11 supergravity:
- Olaf Hohm, Henning Samtleben: Exceptional Field Theory I: covariant Form of M-Theory and Type IIB, Phys. Rev. D 89 066016 (2014) [arXiv:1312.0614, doi:10.1103/PhysRevD.89.066016]
Last revised on September 16, 2024 at 07:53:08. See the history of this page for a list of all contributions to it.