nLab Hadamard gate

Idea

In quantum computing/quantum information theory, by the Hadamard gate one means the quantum logic gate which acts on a single qbit by

$$q_0 \cdot \vert 0 \rangle + q_1 \cdot \vert 1\rangle \;\;\; \mapsto \;\;\; \frac{1}{\sqrt{2}} \big( q_0 + q_1 \big) \cdot \vert 0 \rangle + \frac{1}{\sqrt{2}} \big( q_0 - q_1 \big) \cdot \vert 1 \rangle \,,$$

hence which is the linear map $H \,\colon\, \mathbb{C}^2 \longrightarrow \mathbb{C}^2$ which in the standard linear basis is given by the matrix

$$\frac{1}{\sqrt{2}} \left( \array{ +1 & +1 \\ +1 & -1 } \right) \,.$$

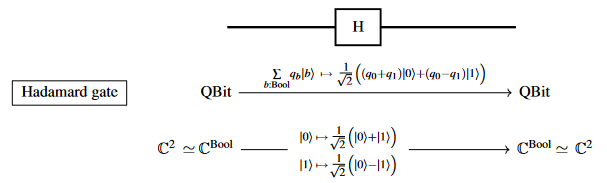
Simple as it is, the Hadamard gate plays a central role in theory and practice of quantum circuits, notably where in its combination with the CNOT gate it is used to produce Bell states (such as in the quantum teleportation protocol).

Related gates

• Pauli gates

• T gates, S gate

• rotation gates

• CNOT gate

• Toffoli gate

References

• Emanuel Knill, p. 10 in: Conventions for quantum pseudocode Los Alamos Technical Report (1996) $[$LA-UR-96-2724, doi:10.2172/366453, pdf, pdf$]$

• Michael A. Nielsen, Isaac L. Chuang, p. 28 in: Quantum computation and quantum information, Cambridge University Press (2000) $[$doi:10.1017/CBO9780511976667, pdf, pdf$]$

See also:

• Wikipedia, Quantum logic – Hadamard gate