nLab rotation gate

Idea

In quantum information theory and quantum computing, by a rotation gate one means a quantum gate acting on a single qbit — regarded as a spinor acted on by SU(2) $\simeq$ Spin(3) — by rotation of any given angle around one of the coordinate 3 axes.

Concretely, the standard notational convention for these gates in the canonical qbit measurement basis is the following (where $X$, $Y$, $Z$ denote the Pauli gates and $\theta \in [0,4\pi)$ is the rotation angle):

$$\begin{array}{ccccccc} R_x(\theta) &\coloneqq& \exp\big( - \mathrm{i} \theta X/2 \big) &=& cos(\theta/2) \, id - \mathrm{i} \, sin(\theta/2) \, X &=& \left[ \begin{array}{cc} cos(\theta/2) & - \mathrm{i} \, sin(\theta/2) \\ - \mathrm{i} \, sin(\theta/2) & cos(\theta/2) \end{array} \right] \\ R_y(\theta) &\coloneqq& \exp\big( - \mathrm{i} \theta Y/2 \big) &=& cos(\theta/2) \, id - \mathrm{i} \, sin(\theta/2) \, Y &=& \left[ \begin{array}{cc} cos(\theta/2) & - sin(\theta/2) \\ - sin(\theta/2) & cos(\theta/2) \end{array} \right] \\ \\ R_z(\theta) &\coloneqq& \exp\big( - \mathrm{i} \theta Z/2 \big) &=& cos(\theta/2) \, id - \mathrm{i} \, sin(\theta/2) \, Z &=& \left[ \begin{array}{cc} e^{-\mathrm{i} \theta/2} & 0 \\ 0 & e^{\mathrm{i}\theta/2} \end{array} \right] \mathrlap{\,.} \end{array}$$

Remark

To appreciate the $4\pi$-domain of the angle variable $\theta$, recall that the action of these linear operators $R_\bullet$ on $\mathbb{C}^2$ is rotation of spinors, double-covering rotation of vectors $(x,y,z) \in \mathbb{R}^3$ which instead is given by the conjugation action:

$$x X + y Y + z Z \;\;\mapsto\;\; R_\bullet(\theta) (x X + y Y + z Z) R_\bullet(-\theta) \,.$$

In particular, in each case $R_\bullet(2\pi) = -1 \in Z\big(Spin(3)\big)$ becomes the identity operation (only) under the spin double cover map $Spin(3)$ $\to$ $SO(3)$.

Applications

Quantum Fourier transform

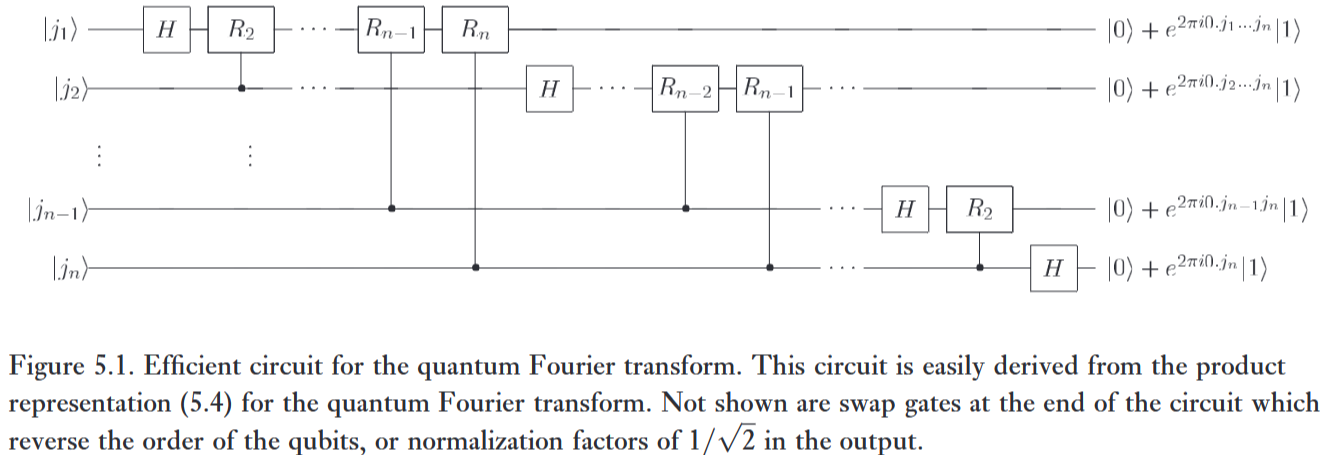
Controlled rotation gates play a key role in the quantum Fourier transform (and thus in many quantum algorithms, notably in Shor's algorithm).

Concretely, quantum circuits implementing the quantum Fourier transform employ many copies [Nielsen & Chuang 2000 (5.11) & Fig. 5.1, pp 218] of the gates

$$R_k \;\coloneqq\; \left[ \begin{array}{c} 1 & 0 \\ 0 & e^{2 \pi \mathrm{i}/2^k} \end{array} \right] \;=\; e^{\pi \mathrm{i}/2^k} \; \left[ \begin{array}{c} e^{-\pi \mathrm{i}/2^k} & 0 \\ 0 & e^{\pi \mathrm{i}/2^k} \end{array} \right] \;=\; e^{\pi \mathrm{i}/2^k} \, R_z(2\pi \mathrm{i}/2^k)$$

for $k \in \mathbb{N}$.

(from Nielsen Chuang 2000)

Related gates

• Pauli gates

• Hadamard gate

• T gate, S gate

• CNOT gate

• Toffoli gate

References

Textbook account:

• Michael A. Nielsen, Isaac L. Chuang, (4.4-6) in: Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]

In Shor's algorithm:

• Austin G. Fowler, Lloyd C. L. Hollenberg: Scalability of Shor’s algorithm with a limited set of rotation gates, Phys. Rev. A 70 (2004) 032329 [arXiv:quant-ph/0306018, doi:10.1103/PhysRevA.70.032329]