nLab RR-field tadpole cancellation

Idea

In the presence of D-branes, plain type II string theory in fact has a quantum anomaly reflected on the worldsheet by tadpole Feynman diagrams in the string perturbation series for RR-fields

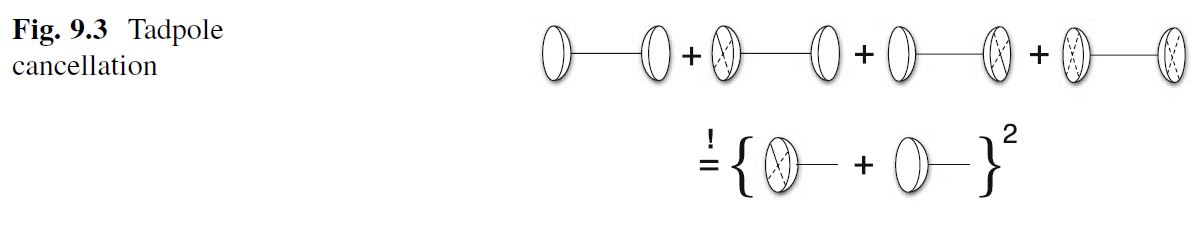
graphics grabbed from Blumenhagen-Lüst-Theisen 13

and reflected in target spacetime by non-trivial total RR-field flux on compact spaces

graphics grabbed from Ibanez-Uranga 12

This anomaly cancels if the D-branes are accompanied by a suitable collection of O-planes, hence if one considers orientifold backgrounds (Sagnotti 88, pp. 5, Gimon-Polchinski 96, section 3). (For space-filling O-planes this means to consider type I string theory instead.)

Accordingly, tadpole cancellation via orientifolding is a key consistency condition in the construction of intersecting D-brane models for string phenomenology.

Traditionally RR-tadpole cancellation is discussed in ordinary cohomology, the common arguments notwithstanding that D-brane charge should be in K-theory.

Discussion of tadpole cancellation with D-brane charge regarded in K-theory was initated in Uranga 00, Section 5, see also Garcia-Uranga 05, Marchesano 03, Section 4, Marchesano-Shiu 04, CKMNW 05, Section 2.2, Maiden-Shiu-Stefanski 06, Section 5, DFM 09, p. 6-7.

But the situation remains somewhat inconclusive (see also Moore 14, p. 21-22).

In plane and toroidal orientifolds

More details are understood in the special case of plane orbifolds $V^{cpt} \!\sslash\! G$ and toroidal orientifolds $\mathbb{T}^V \!\sslash\! G$ where fractional D-branes may be stuck at orbifold/orientifold singularities, whose D-brane charge is supposed to be in the equivariant K-theory of the point, hence the representation ring of the given isotropy group.

In terms of equivariant K-theory / the representation ring

In this case tadpole cancellation conditions are given by representation theoretic equations, constraining the characters of the linear representations corresponding to the fractional D-branes.

Let $G$ be a finite group. Let

$$[1] \subset [H_1] \subset [H_2] \subset \cdots \subset [G]$$

be a linear extension of its partially ordered lattice of conjugacy classes of subgroups, with sub- linear order of cyclic subgroups

$$[1] \subset \left[ \left\langle g_1 \right\rangle \right] \subset \left[ \left\langle g_2 \right\rangle \right] \subset \cdots \subset \left[ \left\langle g_{\vert ConjCl(G)\vert} \right\rangle \right] \,.$$

This way every virtual representation $[V] \in RU(G) = KU_G(\ast)$ (the D-brane charge of a bound state of fractional D-branes/anti-branes) has a character which is a list of complex numbers of the form

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\cdots$	$\left[\langle g_{\vert ConjCl(G)\vert}\rangle\right]$
$\chi_V =$	$dim(V)$	$tr_V\left( g_1\right)$	$tr_V\left(g_2\right)$	$\cdots$	$tr_V\left(g_{\vert ConjCl(G)\vert}\right)$
${{\text{fractional} \atop \text{D-brane/anti-brane}} \atop \text{bound state}}$	${ {\text{mass} =} \atop {{\text{net number} \atop \text{of branes}}}}$	${\text{RR-charge in} \atop {g_1\text{-twisted sector}}}$	${\text{RR-charge in} \atop {g_2\text{-twisted sector}}}$	$\cdots$	$\cdots$

Here $dim(V) \in \mathbb{Z}$ is the mass, hence the net number of fractional D-branes/anti-branes in the bound state, while $tr_V\left(g_k\right)$ is (up to a global rational number-factor $1/{\vert G \vert}$) supposed to be its charge as seen by the RR-fields in the $g_k$-twisted sector.

In fact, since we are dealing with fractional D-branes, both the charge and mass in the above table are in factional units $1/{\vert G\vert}$ of the order of the isotropy group $G$ (by this formula), so that normalized mass and charge is

(1)$$M \;=\; \tfrac{1}{{\vert G\vert}} dim(V) \,, \phantom{AAA} Q_V(g) \;=\; \tfrac{1}{\vert G\vert} \chi_V(g) \coloneqq \tfrac{1}{\vert G\vert} tr_V\left( g\right) \,.$$

Local/twisted tadpole cancellation

The twisted (local) tadpole cancellation condition for fractional D-branes at orbifold singularities is that the RR-charges in all non-trivially twisted sectors vanish:

(2)$$Q_V(g) = 0 \phantom{AA}\text{hence equivalently} \phantom{AA} \chi_{V}\left(g\right) \;=\; 0 \,, \phantom{AAA} g \neq e$$

Example

(regular representation solves tadpole cancellation for fractional D-branes)

For every finite group $G$, the homogeous tadpole cancellation condition (2) is satisfied by all multiples $n \cdot k[G/1]$ of the regular representation $k[G/1]$ (since no non-trivial element $g \in G$ has fixed points when acting on $G$, and using this Prop.). Hence the mass and charge (1) of the fractional D-brane corresponding to the regular representation is

$$M_{{}_{k[G/1]}} \;=\; 1 \,, \phantom{AA} Q_{{}_{k[G/1]}}(g) \;=\; 0 \,.$$

These multiples of the regular representation are regarded as trivial solutions to (2).

Proposition

In fact, the multiples of the regular representation (Example ) are the only solutions to the local/twisted tadpole cancellation condition (2) for fractional D-branes.

Proof

Consider the truncated character morphism

$$Q \cdot {\vert G \vert} \;\colon\; Rep_k(G) \overset{\chi}{\longrightarrow} k^{\left\vert ConjCl(G) \right\vert} \overset{ \text{forget dimension/mass} }{\longrightarrow} k^{\left\vert ConjCl(G)\right\vert -1 } \,.$$

We have to show that the kernel of this map is the free abelian group generated by the regular representation:

$$ker\big( Q \cdot {\vert G \vert} \big) \;\simeq\; \mathbb{Z} \cdot k[G/1] \,.$$

Now over a ground field $k$ of characteristic zero (such as the real numbers or complex numbers, in the case at hand) we have (from this Example) that

1. for $\rho \neq \mathbf{1}$ a non-trivial irreducible representation we have

   $$\underset{g \in G \setminus \{e\}}{\sum} Q_{\rho}(g) \cdot {\vert G \vert} \;\coloneqq\; \underset{g \in G \setminus \{e\}}{\sum} \chi_\rho(g) \;=\; - dim(\rho)$$

2. for $\rho = \mathbf{1}$ the trivial irreducible representation we have

   $$\underset{g \in G \setminus \{e\}}{\sum} Q_{\rho}(g) \cdot {\vert G \vert} \;\coloneqq\; \underset{g \in G \setminus \{e\}}{\sum} \chi_\rho(g) \;=\; {\left\vert G\right \vert} - 1 \;=\; - dim(\mathbf{1}) \;mod\; {\vert G\vert}$$

Since every $V \in R_{k}(G)$ is a $\mathbb{Z}$-linear combination of these irreps, it follows generally that the fractional part of the mass of a fractional D-brane is recovered from its charges:

$$dim(V) \;mod\; {\vert G \vert} \;=\; - \underset{g \in G \setminus \{e\}}{\sum} Q_{V}(g) \cdot {\vert G \vert} \;\coloneqq\; - \underset{g \in G \setminus \{e\}}{\sum} \chi_V(g) \,.$$

But this means that all $V$ in the kernel of $Q \cdot {\vert G \vert}$ must have

$$dim(V) \;=\; 0 \;mod\; {\vert G \vert} \,.$$

This is indeed the case for the multiples $V = n\cdot k[G/1]$ of the regular representation (Example ). Conversely, the injectivity of the full character morphism $\chi$ (this Prop.) says that every $V$ with $dim(V) = n \cdot {\vert G\vert }$ and $Q_V(g) = 0$ must be the $n$th multiple of the regular representation.

Global/untwisted tadpole cancellation

On the other hand, at an orientifold singularity, the O-plane itself carries such charge – O-plane charge (see there):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\cdots$	$\left[\langle g_{\vert ConjCl(G)\vert}\rangle\right]$
$\chi_O =$	$dim(O)$	$tr_O\left( g_1\right)$	$tr_O\left(g_2\right)$	$\cdots$	$tr_O\left(g_{\vert ConjCl(G)\vert}\right)$
$\text{O-plane}$		${\text{O-plane charge in} \atop {g_1\text{-twisted sector}}}$	${\text{O-plane-charge in} \atop {g_2\text{-twisted sector}}}$	$\cdots$	$\cdots$

(These are $O^-$-plane charges. There may also be $O^+$-plane charges. Alternatively, these are $O^-$-branes with a fractional D-brane stuck on them.)

Now the untwisted (global) tadpole cancellation condition is that (all representations are real and) this O-plane charge is cancelled against the D-brane charge:

(3)$$\chi_{V}\left(g_{k \geq 1}\right) \;=\; 0 \phantom{AA} \text{and} \phantom{AA} dim(V) = dim(O) \,.$$

By Prop. the only possible solution of this is the $n$th multiple of the regular representation, if $dim(O)$ is $n$ times the dimension of the regular representation:

(4)$$V = N \cdot k[G/1] \,.$$

In basic examples the O-plane-charge

$$O = 2^{p-4} n \cdot \mathbf{1}$$

is for $n_O$ coincident O-planes is the corresponding multiple by the O-plane charge $\mu_{Op} = -2^{8-4}$ (here) of the trivial irrep, whence a solution to the tadpole cancellation exists if $\frac{2^{p-4}}{\vert G\vert } \in \mathbb{N} \subset \mathbb{Q}$ and is then given by

$$V \;=\; \frac{2^{p-4}}{\vert G\vert } \cdot k[G/1] \,.$$

Sometimes the condition (5) is found with an offset by a trivial representation

(5)$$V = N \cdot k[G/1] + \mathbf{p}_{triv} \,.$$

This corresponds to single fractional D-branes sitting on top of the O-planes, turning $O^-$-planes into $O^+$-planes.

Examples for toroidal orientifolds

RR-field tadpole cancellation conditions for D-branes wrapped on toroidal orientifolds
in terms of their D-brane charge $V \in K_G(\ast) = R_G$ in equivariant K-theory = representation ring
(here $\mathbf{n}_{reg} = k[G/1]$ denotes the regular representation of dimension $n =$ ord(G))

single D-brane species on toroidal orientifold	local/twisted tadpole cancellation condition	global/untwisted tadpole cancellation condition	comment
D5-branes transv. to $\mathbb{T}^{\mathbf{4}_{\mathbb{H}}}\!\sslash\! \mathbb{Z}_{2}$	$V = N \cdot \mathbf{2}_{reg}$ (Buchel-Shiu-Tye 99 (19))	$V = 16 \cdot \mathbf{2}_{reg}$ (Buchel-Shiu-Tye 99 (18))	following Gimon-Polchinski 96, Gimon-Johnson 96
D5-branes transv. to $\mathbb{T}^{\mathbf{4}_{\mathbb{H}}} \!\sslash\! \mathbb{Z}_{4}$	$V = N \cdot \mathbf{4}_{reg}$ (Buchel-Shiu-Tye 99 (19))	$V = 8 \cdot \mathbf{4}_{reg}$ (Buchel-Shiu-Tye 99 (18))	following Gimon-Polchinski 96, Gimon-Johnson 96
D4-branes transv. to $\mathbb{T}^{\mathbf{1}_{\mathrm{triv}} + \mathbf{4}_{\mathbb{H}}} \!\sslash\! \mathbb{Z}_k$	$V = N \cdot \mathbf{k}_{reg}$ (AFIRU 00a, 4.2.1)
D4-branes transv. to $\mathbb{T}^{\mathbf{1}_{\mathrm{triv}} + \mathbf{4}_{\mathbb{H}}} \!\sslash\! \mathbb{Z}_3$	$V = N \cdot \mathbf{3}_{reg}$ (AFIRU 00b, (7.2))	$V = 4 \cdot \mathbf{3}_{reg} + 4 \cdot \mathbf{1}_{triv}$ (Kataoka-Shimojo 01, (14)-(17)
D8-branes on $\mathbb{T}^{\mathbf{1}_{\mathrm{triv}} + \mathbf{4}_{\mathbb{H}}} \!\sslash\! \mathbb{Z}_3$	$V = N \cdot \mathbf{3}_{reg}$	$V = 4 \cdot \mathbf{3}_{reg} + 4 \cdot \mathbf{1}_{triv}$ (Honecker 01, 4, Honecker 02a, (25) ∧ (28) ⇔ (29), Honecker 02b, (3.19)-(3.27))	equivalent to D4 case by T-duality: Honecker 01, p. 2, Honecker 02a, 6, Honecker 02b, p. 15 review in: Marchesano 03, Sec. 4
D6-branes on $\mathbb{T}^6 \!\sslash\! \mathbb{Z}_4$		$V = 8 \cdot \mathbf{4}_{reg}$ (Ishihara-Kataoka-Sato 99, (4.16))
D3-branes on $\mathbb{T}^{\mathbf{4}_{\mathbb{H}}} \!\sslash\! \mathbb{Z}_k$	$V = N \cdot \mathbf{k}_{reg}$ (Feng-He-Karch-Uranga 01, (25))
D7-branes on $\mathbb{T}^{\mathbf{4}_{\mathbb{H}}} \!\sslash\! \mathbb{Z}_k$	$V = N \cdot \mathbf{k}_{reg}$ (Feng-He-Karch-Uranga 01, (5), (6))

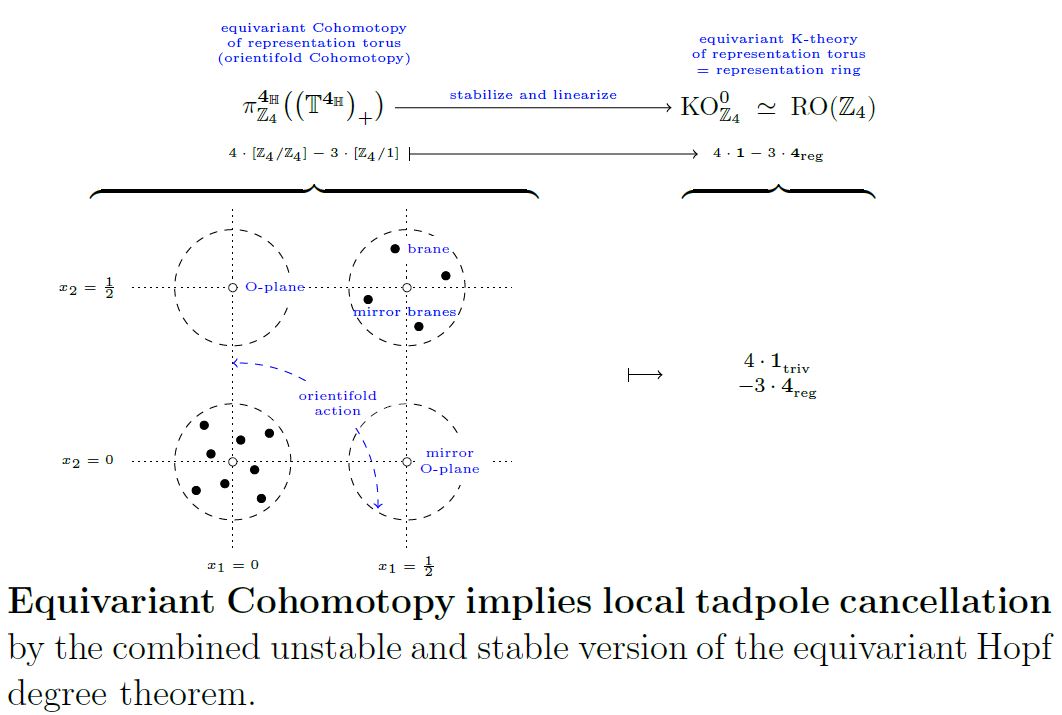
graphics grabbed from Sati-Schreiber 19

See also at equivariant Hopf degree theorem.

graphics grabbed from Sati-Schreiber 19

Examples of non-compact singularities

We discuss more explicitly the solutions to the local/twisted tadpole cancellation condition (2) for fractional D-branes at orbifold singularities for isotropy group one of the non-abelian finite subgroups of SU(2),

$$G_{DE} \;\subset\; SU(2)$$

hence those in the D- and E-series, hence the binary dihedral groups $2 D_{2n}$ and the three exceptional cases: 2T, 2O and 2I.

For these groups, by BSS 18, Theorem 4.1 the virtual permutation representations span precisely the sub charge lattice of integral (non-irrational) characters/RR-charges in the orientifold charge lattice of the corresponding ADE-singularity, namely of the equivariant KO-theory=real representation ring

$$KO^0_{G_{DE}}(\ast) \;=\; RO\left( G_{DE} \right) \,.$$

Since the tadpole cancellation condition (2) in particular requires the characters/charges to be integral (specifically: zero) the general solution to the tadpole cancellation condition is indeed in this sub-lattice, and so that is where we may and do solve it, below.

In accord with the general Prop. we find that in each case there is precisely a 1-dimensional (i.e. $\simeq \mathbb{Z}$) sublattice of the charge lattice (the representation ring) which solves the twisted tadpole cancellation condition (2), hence a sublattice given by the integer-multiples $N \cdot V_0$ of one single fractional D-brane bound state $V_0 \in KO^0_G(\ast)$. There are then necessarily two of these generators $\pm V_0$. We check below that in all cases the normalized mass of these is $\pm$ unity, as it must be for the regular representation, by Prop. .

At a $\mathbb{Z}_2$-orientifold singularity

For $G = \mathbb{Z}_2$ the cyclic group of order ${\vert \mathbb{Z}_2\vert} = 2$, the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (e.g. here)

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$-1$

One sees immediately that the general solution to the local/twisted tadpole cancellation condition (2) for $G = \mathbb{Z}_2$ is

$$V \;=\; n \cdot \Big( 1 \cdot V_1 + 1 \cdot V_2 \Big) \,, \phantom{AAA} n \in \mathbb{Z} \,.$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{\mathbb{Z}_2} & = dim(V) / {\vert \mathbb{Z}_2 \vert } \\ & = \chi_V([\langle e\rangle]) / {\vert \mathbb{Z}_2 \vert} \\ & = \big( 1 \cdot 1 + 1 \cdot 1 \big) / {2} & \\ & = 2 / 2 \\ & = 1 \end{aligned}$$

At a $\mathbb{Z}_4$-orientifold singularity

For $G = \mathbb{Z}_4$ the cyclic group of order 4, the characters/D-brane charges of the complex irreducible representations/fractional D-branes are (e.g. here)

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$
$\chi_{V_3} =$	$\phantom{-}1$	$-1$	$-i$	$\phantom{-}i$
$\chi_{V_4} =$	$\phantom{-}1$	$-1$	$\phantom{-}i$	$-i$

One sees immediately that the general solution to the local/twisted tadpole cancellation condition (2) for $G = \mathbb{Z}_3$ is

$$V \;=\; n \cdot \Big( 1 \cdot V_1 + 1 \cdot V_2 + 1 \cdot V_3 + 1 \cdot V_4 \Big) \,, \phantom{AAA} n \in \mathbb{Z} \,.$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{\mathbb{Z}_4} & = dim(V) / {\vert \mathbb{Z}_4 \vert } \\ & = \chi_V([\langle e\rangle]) / {\vert \mathbb{Z}_4 \vert} \\ & = \big( 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 \big) / {4} & \\ & = 4 / 4 \\ & = 1 \end{aligned}$$

At a $2 D_4$-orientifold singularity

For $G = 2 D_4 = Q_8$ the binary dihedral group of order ${\vert 2 D_4\vert}$ (equivalently: the quaternion group), the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.1):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$\phantom{-}1$	$-1$
$\chi_{V_3} =$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$\phantom{-}1$
$\chi_{V_4} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$
$\chi_{V_5} =$	$\phantom{-}4$	$-4$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$

One sees (here) that the general solution to the local/twisted tadpole cancellation condition (2) for $G =2 D_4$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 1 \cdot V_3 + 1 \cdot V_4 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2 D_4} & = dim(V)/ {\vert 2 D_4\vert} \\ & = \chi_V\left( [\langle e\rangle]\right) / {\vert 2 D_4\vert} & = \big( 1 + 1 + 1 + 1 + 4 \big) / 8 \\ & = 8 / 8 \\ & = 1 \end{aligned}$$

At a $2 D_6$-orientifold singularity

For $G = 2 D_6$ the binary dihedral group of order ${\vert 2 D_6\vert} = 12$, the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.2):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$\phantom{-}1$
$\chi_{V_3} =$	$\phantom{-}2$	$\phantom{-}2$	$-1$	$\phantom{-}0$	$\phantom{-}0$	$-1$
$\chi_{V_4} =$	$\phantom{-}2$	$-2$	$\phantom{-}2$	$\phantom{-}0$	$\phantom{-}0$	$-2$
$\chi_{V_5} =$	$\phantom{-}4$	$-4$	$-2$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}2$

One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for $G =2 D_6$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 2 \cdot V_3 + 1 \cdot V_4 + 1 \cdot V_5 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2 D_6} & = dim(V) / {\vert 2 D_6 \vert } \\ & = \chi_V([\langle e\rangle]) / {\vert 2 D_6\vert} \\ & = \big( 1 \cdot 1 + 1 \cdot 1 + 2 \cdot 2 + 1 \cdot 2 + 1 \cdot 4 \big) / {12} & \\ & = 12 / 12 \\ & = 1 \end{aligned}$$

At a $2 D_8$-orientifold singularity

For $G = 2 D_8$ the binary dihedral group of order ${\vert 2 D_8\vert} = 16$, the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.3):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$	$\left[\langle g_6\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$\phantom{-}1$	$-1$	$-1$
$\chi_{V_3} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_4} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$-1$
$\chi_{V_5} =$	$\phantom{-}2$	$\phantom{-}2$	$-2$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$
$\chi_{V_6} =$	$\phantom{-}8$	$-8$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$

One finds (here), that the general solution to the local/twisted tadpole cancellation condition (2) for $G =2 D_8$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 1 \cdot V_3 + 1 \cdot V_4 + 2 \cdot V_5 + 1 \cdot V_6 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2 D_8} & = dim(V) / {\vert 2 D_8\vert} \\ & = \chi_V([\langle e\rangle]) / { \vert 2 D_8\vert } \\ & = \big( 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 + 2 \cdot 2 + 1 \cdot 8 \big) / 16 & \\ & = 16 / 16 \\ & = 1 \end{aligned}$$

At a $2 D_{10}$-orientifold singularity

For $G = 2 D_{10}$ the binary dihedral group of order ${\vert 2 D_{10}\vert} = 20$, the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.4):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$	$\left[\langle g_6\rangle\right]$	$\left[\langle g_7\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_3} =$	$\phantom{-}2$	$-2$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}2$	$\phantom{-}2$	$-2$	$-2$
$\chi_{V_4} =$	$\phantom{-}4$	$\phantom{-}4$	$\phantom{-}0$	$\phantom{-}0$	$-1$	$-1$	$-1$	$-1$
$\chi_{V_5} =$	$\phantom{-}8$	$-8$	$\phantom{-}0$	$\phantom{-}0$	$-2$	$-2$	$\phantom{-}2$	$\phantom{-}2$

One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for $G =2 D_{10}$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 1 \cdot V_3 + 2 \cdot V_4 + 1 \cdot V_5 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2 D_{10}} & = dim(V) / {\vert 2 D_{10}\vert} \\ & = \chi_V([\langle e\rangle]) / {\vert 2 D_{10}\vert} \\ & = \big( 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 2 + 2 \cdot 4 + 1 \cdot 8 \big) / 20 & \\ & = 20 / 20 \\ & = 1 \end{aligned}$$

At a $2 D_{12}$-orientifold singularity

For $G = 2 D_{12}$ the binary dihedral group of order ${\vert 2 D_{12}\vert} = 24$, the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.5):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$	$\left[\langle g_6\rangle\right]$	$\left[\langle g_7\rangle\right]$	$\left[\langle g_8\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_3} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$\phantom{-}1$	$-1$	$\phantom{-}1$	$-1$	$-1$
$\chi_{V_4} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$\phantom{-}1$	$-1$	$-1$
$\chi_{V_5} =$	$\phantom{-}2$	$\phantom{-}2$	$-1$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}2$	$-1$	$-1$	$-1$
$\chi_{V_6} =$	$\phantom{-}2$	$\phantom{-}2$	$-1$	$\phantom{-}0$	$\phantom{-}0$	$-2$	$-1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_7} =$	$\phantom{-}4$	$-4$	$\phantom{-}4$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$-4$	$\phantom{-}0$	$\phantom{-}0$
$\chi_{V_8} =$	$\phantom{-}8$	$-8$	$-4$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}4$	$\phantom{-}0$	$\phantom{-}0$

One sees (here) that the general solution to the local/twisted tadpole cancellation condition (2) for $G =2 D_{12}$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 1 \cdot V_3 + 1 \cdot V_4 + 2 \cdot V_5 + 2 \cdot V_6 + 1 \cdot V_7 + 1 \cdot V_8 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2 D_{12}} & = dim(V) / {\vert 2 D_{12}\vert } \\ & = \chi_V([\langle e\rangle]) / {\vert 2 D_{12}\vert } \\ & = \big( 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 + 2 \cdot 2 + 2 \cdot 2 + 1 \cdot 4 + 1 \cdot 8 \big) / 24 & \\ & = 24 / 24 \\ & = 1 \end{aligned}$$

At a $2 D_{14}$-orientifold singularity

For $G = 2 D_{14}$ the binary dihedral group of order ${\vert 2 D_{14}\vert} = 28$, the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.6):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$	$\left[\langle g_6\rangle\right]$	$\left[\langle g_7\rangle\right]$	$\left[\langle g_8\rangle\right]$	$\left[\langle g_9\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_3} =$	$\phantom{-}2$	$-2$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}2$	$\phantom{-}2$	$\phantom{-}2$	$-2$	$-2$	$-2$
$\chi_{V_4} =$	$\phantom{-}6$	$\phantom{-}6$	$\phantom{-}0$	$\phantom{-}0$	$-1$	$-1$	$-1$	$-1$	$-1$	$-1$
$\chi_{V_5} =$	$\phantom{-1}\mathllap{12}$	$\phantom{-1}\mathllap{-12}$	$\phantom{-}0$	$\phantom{-}0$	$-2$	$-2$	$-2$	$\phantom{-}2$	$\phantom{-}2$	$\phantom{-}2$

One sees by immediate inspection, that the general solution to the local/twisted tadpole cancellation condition (2) for $G =2 D_{14}$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 1 \cdot V_3 + 2 \cdot V_4 + 1 \cdot V_5 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2 D_{14}} & = dim(V) / {\vert 2 D_{14}\vert } \\ & = \chi_V([\langle e\rangle]) / {\vert 2 D_{14}\vert } \\ & = \big( 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 2 + 2 \cdot 6 + 1 \cdot 12 \big) / 28 \\ & = 28 /28 \\ & = 1 \end{aligned}$$

At a $2 D_{16}$-orientifold singularity

For $G = 2 D_{16}$ the binary dihedral group of order ${\vert 2 D_{16}\vert} = 32$, the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.7):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$	$\left[\langle g_6\rangle\right]$	$\left[\langle g_7\rangle\right]$	$\left[\langle g_8\rangle\right]$	$\left[\langle g_9\rangle\right]$	$\left[\langle g_9\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$-1$	$-1$
$\chi_{V_3} =$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_4} =$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$	$-1$	$-1$
$\chi_{V_5} =$	$\phantom{-}2$	$\phantom{-}2$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}2$	$-2$	$-2$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$
$\chi_{V_6} =$	$\phantom{-}4$	$\phantom{-}4$	$\phantom{-}0$	$\phantom{-}0$	$-4$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$
$\chi_{V_7} =$	$\phantom{-1}\mathllap{16}$	$\phantom{-1}\mathllap{-16}$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}0$

One sees by immediate inspection, that the general solution to the local/twisted tadpole cancellation condition (2) for $G =2 D_{16}$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 1 \cdot V_3 + 1 \cdot V_4 + 2 \cdot V_5 + 2 \cdot V_6 + 1 \cdot V_7 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2 D_{16}} & = dim(V) / {\vert 2 D_{16}\vert} \\ & = \chi_V([\langle e\rangle]) / {\vert 2 D_{16}\vert} \\ & = \big( 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 + 2 \cdot 2 + 2 \cdot 4 + 1 \cdot 16 \big) /32 \\ & = 32 / 32 \\ & = 1 \end{aligned}$$

At a $2 T$-orientifold singularity

For $G = 2 T$ the binary tetrahedral group (whose order is ${\vert 2T \vert} =24$), the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.8):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$	$\left[\langle g_6\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}2$	$\phantom{-}2$	$-1$	$-1$	$\phantom{-}2$	$-1$	$-1$
$\chi_{V_3} =$	$\phantom{-}3$	$\phantom{-}3$	$\phantom{-}0$	$\phantom{-}0$	$-1$	$\phantom{-}0$	$\phantom{-}0$
$\chi_{V_4} =$	$\phantom{-}4$	$-4$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}0$	$-1$	$-1$
$\chi_{V_5} =$	$\phantom{-}4$	$-4$	$-2$	$-2$	$\phantom{-}0$	$\phantom{-}2$	$\phantom{-}2$

One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for $G = 2T$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 3 \cdot V_3 + 2 \cdot V_4 + 1 \cdot V_5 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2I} & = dim(V) / {\vert 2 I \vert } \\ & = \chi_V([\langle e\rangle]) / {\vert 2 I \vert } \\ & = \big( 1 \cdot 1 + 1 \cdot 2 + 3 \cdot 3 + 2 \cdot 4 + 1 \cdot 4 \big) / 24 & \\ & = 24 / 24 \\ & = 1 \end{aligned}$$

At a $2 O$-orientifold singularity

For $G = 2 O$ the binary octahedral group (whose order is ${\vert 2O \vert} = 48$), the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.9):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$	$\left[\langle g_6\rangle\right]$	$\left[\langle g_7\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$-1$	$\phantom{-}1$	$-1$	$-1$
$\chi_{V_3} =$	$\phantom{-}2$	$\phantom{-}2$	$-1$	$\phantom{-}2$	$\phantom{-}0$	$-1$	$\phantom{-}0$	$\phantom{-}0$
$\chi_{V_4} =$	$\phantom{-}3$	$\phantom{-}3$	$\phantom{-}0$	$-1$	$\phantom{-}1$	$\phantom{-}0$	$-1$	$-1$
$\chi_{V_5} =$	$\phantom{-}3$	$\phantom{-}3$	$\phantom{-}0$	$-1$	$-1$	$\phantom{-}0$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_6} =$	$\phantom{-}8$	$-8$	$\phantom{-}2$	$\phantom{-}0$	$\phantom{-}0$	$-2$	$\phantom{-}0$	$\phantom{-}0$
$\chi_{V_7} =$	$\phantom{-}8$	$-8$	$-4$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}4$	$\phantom{-}0$	$\phantom{-}0$

One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for $G = 2O$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 1 \cdot V_2 + 2 \cdot V_3 + 3 \cdot V_4 + 3 \cdot V_5 + 2 \cdot V_6 + 1 \cdot V_7 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2O} & = dim(V) / {\vert 2 O \vert } \\ & = \chi_V([\langle e\rangle]) / {\vert 2 O \vert } \\ & = \big( 1 \cdot 1 + 1 \cdot 1 + 2 \cdot 2 + 3 \cdot 3 + 3 \cdot 3 + 2 \cdot 8 + 1 \cdot 8 \big) / 48 & \\ & = 48 / 48 \\ & = 1 \end{aligned}$$

At a $2 I$-orientifold singularity

For $G = 2 I$ the binary icosahedral group (whose order is ${\vert 2I \vert} = 120$), the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.10):

$[H] =$	$\left[\langle e\rangle\right]$	$\left[\langle g_1\rangle\right]$	$\left[\langle g_2\rangle\right]$	$\left[\langle g_3\rangle\right]$	$\left[\langle g_4\rangle\right]$	$\left[\langle g_5\rangle\right]$	$\left[\langle g_6\rangle\right]$	$\left[\langle g_7\rangle\right]$	$\left[\langle g_8\rangle\right]$
$\chi_{V_1} =$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_2} =$	$\phantom{-}4$	$\phantom{-}4$	$\phantom{-}1$	$\phantom{-}0$	$-1$	$-1$	$\phantom{-}1$	$-1$	$-1$
$\chi_{V_3} =$	$\phantom{-}5$	$\phantom{-}5$	$-1$	$\phantom{-}1$	$\phantom{-}0$	$\phantom{-}0$	$-1$	$\phantom{-}0$	$\phantom{-}0$
$\chi_{V_4} =$	$\phantom{-}6$	$\phantom{-}6$	$\phantom{-}0$	$-2$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}0$	$\phantom{-}1$	$\phantom{-}1$
$\chi_{V_5} =$	$\phantom{-1}\mathllap{12}$	$\phantom{-1}\mathllap{-12}$	$\phantom{-}0$	$\phantom{-}0$	$\phantom{-}2$	$\phantom{-}2$	$\phantom{-}0$	$-2$	$-2$
$\chi_{V_6} =$	$\phantom{-}8$	$-8$	$\phantom{-}2$	$\phantom{-}0$	$-2$	$-2$	$-2$	$\phantom{-}2$	$\phantom{-}2$
$\chi_{V_7} =$	$\phantom{-}8$	$-8$	$-4$	$\phantom{-}0$	$-2$	$-2$	$\phantom{-}4$	$\phantom{-}2$	$\phantom{-}2$

One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for $G = 2I$ is

$$V \;=\; n \Big( 1 \cdot V_1 + 4 \cdot V_2 + 5 \cdot V_3 + 3 \cdot V_4 + 3 \cdot V_5 + 2 \cdot V_6 + 1 \cdot V_7 \Big) \,, \phantom{AAA} n \in \mathbb{Z}$$

whose minimal positive mass (net brane number) is

$$\begin{aligned} M_{2I} & = dim(V) / {\vert 2I \vert } \\ & = \chi_V([\langle e\rangle]) / {\vert 2I \vert } \\ & = \big( 1 \cdot 1 + 4 \cdot 4 + 5 \cdot 5 + 3 \cdot 6 + 3 \cdot 12 + 2 \cdot 8 + 1 \cdot 8 \big) / 120 \\ & = 120 / 120 \\ & = 1 \end{aligned}$$

Related concepts

• C-field tadpole cancellation in M-theory

• 24 branes transverse to K3 in F-theory and HET-theory

References

General

The issue was first highlighted in

• Augusto Sagnotti, Open strings and their symmetry groups in G. Mack et. al. (eds.) Cargese ’87, “Non-perturbative Quantum Field Theory,” (Pergamon Press, 1988) p. 521 (arXiv:hep-th/0208020)

The argument is recalled in

• Eric Gimon, Joseph Polchinski, section 3 of Consistency Conditions for Orientifolds and D-Manifolds, Phys.Rev.D54:1667-1676, 1996 (arXiv:hep-th/9601038)

Details are in

• Edward Witten, section 9.3 of Superstring Perturbation Theory Revisited (arXiv:1209.5461)

Textbook accounts include

• Luis Ibáñez, Angel Uranga, section 4.4 of String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge 2012

• Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, section 9.4 of Basic Concepts of String Theory Part of the series Theoretical and Mathematical Physics, Springer 2013

Quick illustrations include:

• Marcus Berg, p. 26-36 in Introduction to Orientifolds (pdf, pdf)

• slide 18 here

Critical outlook in

• Gregory Moore p. 21-22 of Physical Mathematics and the Future, talk at Strings 2014 (talk slides, companion text pdf, pdf)

The above discussion follows and character tables for virtual permutation representations above are taken from

• Simon Burton, Hisham Sati, Urs Schreiber, Lift of fractional D-brane charge to equivariant Cohomotopy theory, Journal of Geometry and Physics 161 (2021) 104034 [arXiv:1812.09679, Python code, doi:10.1016/j.geomphys.2020.104034]

• Hisham Sati, Urs Schreiber, Equivariant Cohomotopy implies orientifold tadpole cancellation, Journal of Geometry and Physics 156 (2020) 103775 [arXiv:1909.12277, doi:10.1016/j.geomphys.2020.103775]

See also

• G. Aldazabal, D. Badagnani, Luis Ibáñez, Angel Uranga, Tadpole versus anomaly cancellation in $D=4,6$ compact IIB orientifolds, JHEP 9906:031, 1999 (arXiv:hep-th/9904071)

• Angel Uranga, D-brane probes, RR tadpole cancellation and K-theory charge, Nucl.Phys.B598:225-246, 2001 (arXiv:hep-th/0011048)

• Maria E. Angulo, David Bailin, Huan-Xiong Yang, Tadpole and Anomaly Cancellation Conditions in D-brane Orbifold Models, Int.J.Mod.Phys.A18:3637-3694, 2003 (arXiv:hep-th/0210150)

• Fernando Marchesano, section 4 of Intersecting D-brane Models (arXiv:hep-th/0307252)

• Fernando Marchesano, Gary Shiu, Building MSSM Flux Vacua, JHEP0411:041, 2004 (arXiv:hep-th/0409132)

• C.-M. Chen, G. V. Kraniotis, V. E. Mayes, D. V. Nanopoulos, J. W. Walker, A K-theory Anomaly Free Supersymmetric Flipped SU(5) Model from Intersecting Branes, Phys.Lett. B625 (2005) 96-105 (arXiv:hep-th/0507232)

• Inaki Garcia-Etxebarria, Angel Uranga, From F/M-theory to K-theory and back, JHEP 0602:008, 2006 (arXiv:hep-th/0510073)

• John Maiden, Gary Shiu, Bogdan Stefanski, D-brane Spectrum and K-theory Constraints of D=4, N=1 Orientifolds, JHEP0604:052,2006 (arXiv:hep-th/0602038)

• Tetsuji Kimura, Mitsuhisa Ohta, Kei-Jiro Takahashi, Type IIA orientifolds and orbifolds on non-factorizable tori, Nucl. Phys. B 798 (2008) 89-123 [arXiv:0712.2281, doi:10.1016/j.nuclphysb.2008.01.030]

• Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory, Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)

In view of consistency of flux compactifications:

• Philip Betzler, Erik Plauschinn, Type IIB flux vacua and tadpole cancellation (arXiv:1905.08823)

For the topological string:

• Johannes Walcher, Evidence for Tadpole Cancellation in the Topological String, Communications in Number Theory and Physics 3 1 (2009) [arXiv:0712.2775]

Examples and Models

Specifically K3 orientifolds ($\mathbb{T}^4/G_{ADE}$) in type IIB string theory, hence for D9-branes and D5-branes:

• Eric Gimon, Joseph Polchinski, Section 3.2 of: Consistency Conditions for Orientifolds and D-Manifolds, Phys. Rev. D54: 1667-1676, 1996 (arXiv:hep-th/9601038)

• Eric Gimon, Clifford Johnson, K3 Orientifolds, Nucl. Phys. B477: 715-745, 1996 (arXiv:hep-th/9604129)

• Alex Buchel, Gary Shiu, S.-H. Henry Tye, Anomaly Cancelations in Orientifolds with Quantized B Flux, Nucl.Phys. B569 (2000) 329-361 (arXiv:hep-th/9907203)

• P. Anastasopoulos, A. B. Hammou, A Classification of Toroidal Orientifold Models, Nucl. Phys. B729:49-78, 2005 (arXiv:hep-th/0503044)

Specifically K3 orientifolds ($\mathbb{T}^4/G_{ADE}$) in type IIA string theory, hence for D8-branes and D4-branes:

• J. Park, Angel Uranga, A Note on Superconformal N=2 theories and Orientifolds, Nucl. Phys. B542:139-156, 1999 (arXiv:hep-th/9808161)

• G. Aldazabal, S. Franco, Luis Ibanez, R. Rabadan, Angel Uranga, D=4 Chiral String Compactifications from Intersecting Branes, J. Math. Phys. 42:3103-3126, 2001 (arXiv:hep-th/0011073)

• G. Aldazabal, S. Franco, Luis Ibanez, R. Rabadan, Angel Uranga, Intersecting Brane Worlds, JHEP 0102:047, 2001 (arXiv:hep-ph/0011132)

• H. Kataoka, M. Shimojo, $SU(3) \times SU(2) \times U(1)$ Chiral Models from Intersecting D4-/D5-branes, Progress of Theoretical Physics, Volume 107, Issue 6, June 2002, Pages 1291–1296 (arXiv:hep-th/0112247, doi:10.1143/PTP.107.1291)

The $\mathbb{Z}_N$ action with even $N$ contains an order 2 element $[ ...]$ Then there will be D8-branes in the type IIA D4-brane theory. Since the concept of intersecting D-branesinvolves use of the same dimensional D-branes, we restrict ourselves to the case that the order $N$ of $\mathbb{Z}_N$ is odd. (p. 4)

• Gabriele Honecker, Non-supersymmetric Orientifolds with D-branes at Angles, Fortsch.Phys. 50 (2002) 896-902 (arXiv:hep-th/0112174)

• Gabriele Honecker, Intersecting brane world models from D8-branes on $(T^2 \times T^4/\mathbb{Z}_3)/\Omega\mathcal{R}_1$ type IIA orientifolds, JHEP 0201 (2002) 025 (arXiv:hep-th/0201037)

• Gabriele Honecker, Non-supersymmetric orientifolds and chiral fermions from intersecting D6- and D8-branes, thesis 2002 (pdf)

The Witten-Sakai-Sugimoto model on D4-D8-brane bound states for QCD with orthogonal gauge groups on O-planes:

• Toshiya Imoto, Tadakatsu Sakai, Shigeki Sugimoto, $O(N)$ and $USp(N)$ QCD from String Theory, Prog.Theor.Phys.122:1433-1453, 2010 (arXiv:0907.2968)

• Hee-Cheol Kim, Sung-Soo Kim, Kimyeong Lee, 5-dim Superconformal Index with Enhanced $E_n$ Global Symmetry, JHEP 1210 (2012) 142 (arXiv:1206.6781)

Specifically D5 brane models T-dual to D6/D8 models:

• Angel Uranga, A New Orientifold of $\mathbb{C}^2/\mathbb{Z}_N$ and Six-dimensional RG Fixed Points, Nucl. Phys. B577:73-87, 2000 (arXiv:hep-th/9910155)

• Bo Feng, Yang-Hui He, Andreas Karch, Angel Uranga, Orientifold dual for stuck NS5 branes, JHEP 0106:065, 2001 (arXiv:hep-th/0103177)

Specifically for D6-branes:

• S. Ishihara, H. Kataoka, Hikaru Sato, $D=4$, $N=1$, Type IIA Orientifolds, Phys. Rev. D60 (1999) 126005 (arXiv:hep-th/9908017)

• Mirjam Cvetic, Paul Langacker, Tianjun Li, Tao Liu, D6-brane Splitting on Type IIA Orientifolds, Nucl. Phys. B709:241-266, 2005 (arXiv:hep-th/0407178)

Specifically for D3-branes/D7-branes:

• Feng-He-Karch-Uranga 01

Various:

• Dieter Lüst, S. Reffert, E. Scheidegger, S. Stieberger, Resolved Toroidal Orbifolds and their Orientifolds, Adv.Theor.Math.Phys.12:67-183, 2008 (arXiv:hep-th/0609014)