nLab spin representation
Context
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Spin geometry
spin geometry, string geometry, fivebrane geometry …
Ingredients
Spin geometry
rotation groups in low dimensions:
see also
String geometry
Fivebrane geometry
Ninebrane geometry
Contents
- Idea
- Definition
- Properties
- Complex representations
- Real representations (Majorana representations)
- Spinor bilinear forms
- – spinor metric
- – super Poincaré bracket (supersymmetry)
- Over the complex numbers
- Over the real numbers (for Majorana spinors)
- Pairing to a vector in terms of the charge conjugation matrix
- Counting numbers of supersymmetries
- – superconformal bracket
- Expression of real representations via real normed division algebras
- Related entries
- References
Idea
A representation of the spin group.
Definition
Definition
A quadratic vector space is a vector space of finite dimension over a field of characteristic 0, and equipped with a symmetric bilinear form .
Conventions as in (Varadarajan 04, section 5.3).
We write for the corresponding quadratic form.
Definition
The Clifford algebra of a quadratic vector space, def. , is the associative algebra over which is the quotient
of the tensor algebra of by the ideal generated by the elements .
Since the tensor algebra is naturally -graded, the Clifford algebra is naturally -graded.
Let be the -dimensional Cartesian space with its canonical scalar product. Write for the complexification of its Clifford algebra.
Definition
The Spin group of a quadratic vector space, def. , is the subgroup of the group of units in the Clifford algebra
on those elements which are even number multiples of elements with .
Specifically, “the” Spin group is
A spin representation is a linear representation of the spin group, def. .
Properties
Complex representations
Complex representations of the spin group follow a mod-2 Bott periodicity.
In even there are two inequivalent complex-linear irreducible representations of , each of complex dimension , called the two chiral representations, or the two Weyl spinor representations.
For instance for one often writes these as and .
The direct sum of the two chiral representation is called the Dirac spinor representation, for instance .
In odd there is a single complex irreducible representation of complex dimension . For instance for one often writes this as . This is called the Dirac spinor representation in this odd dimension.
For , if denote the generators of the Clifford algebra then there is the chirality operator
on the Dirac representation, whose eigenspaces induce its decomposition into the two chiral summands.
The unique irreducible Dirac representation in the odd dimension is, as a complex vector space, the sum of the two chiral representations in dimension , with the Clifford algebra represented by through acting diagonally on the two chiral representations, and the chirality operator in dimension acting on their sum, now being the representation of the st Clifford algebra generator.
Real representations (Majorana representations)
One may ask in which dimensions the above complex representations admit a real structure
Real spinor representations are also called Majorana representations (with variants such as “symplectic Majorana”), and an element of a real/Majorana spin representation is also called a Majorana spinor. On a Majorana representation there is a non-vanishing symmetric and -invariant bilinear form , projectively unique if is irreducible. This serves as the odd-odd Lie bracket in the super Lie algebra called the super Poincaré Lie algebra extension of the ordinary Poincaré Lie algebra induced by . This is “supersymmetry” in physics.
The above irreducible complex representations admit a real structure for . Therefore in dimension there exist Majorana-Weyl spinor representations.
The above irreducible complex representations admit a quaternionic structure for .
Let be a quadratic vector space, def. , over the real numbers with bilinear form of Lorentzian signature, hence is Minkowski spacetime of some dimension .
The following table lists the irreducible real representations of (Freed 99, page 48).
| minimal real spin representation | in terms of | supergravity | |||
|---|---|---|---|---|---|
| 1 | real | 1 | |||
| 2 | real | 1 | |||
| 3 | real | 2 | |||
| 4 | 4 | d=4 N=1 supergravity | |||
| 5 | 8 | ||||
| 6 | SL(2,H) | 8 | |||
| 7 | 16 | ||||
| 8 | 16 | ||||
| 9 | real | 16 | |||
| 10 | real | 16 | type II supergravity | ||
| 11 | real | 32 | 11-dimensional supergravity |
Here is the 2-dimensional complex vector space on which the quaternions naturally act.
Remark
The last column implies that in each dimension there exists a linear map
which is
-
symmetric;
-
-equivariant.
This allows to form the super Poincaré Lie algebra in each of these cases. See there and see Spinor bilinear forms below for more.
Spinor bilinear forms
Let be a quadratic vector space, def. . For write for its th skew-symmetrized tensor power, regarded naturally as a representation of the spin group .
For two irreducible representations of , we discuss here homomorphisms of representations (hence -linear maps respecting the -action) of the form
These appear notably in the following applications:
-
for symmetric bilinears define a metric on the space of spinors, also known as a charge conjugation matrix. This appears for instance in the Lagrangian for a spinor field , which is of the form , for a Dirac operator;
-
for symmetric bilinear -homomorphisms constitutes the odd-odd Lie bracket in a super Poincaré Lie algebra extension of the a Poincaré Lie algebra by .
-
for symmetric bilineat spin pairings appear as the odd-odd bracket in a superconformal super Lie algebra;
-
for higher spin bilinears appear in further polyvector extensions.
– spinor metric
We discuss spinor bilinear pairings to scalars.
Over the complex numbers
Proposition
Let be a quadratic vector space, def. over the complex numbers of dimension . Then there exists in dimensions , up to rescaling, a unique -invariant bilinear form
on a complex irreducible representation of , or in dimension 2 and 6 a bilinear pairing
which is non-degenerate and whose symmetry is given by the following table:
| C | |
|---|---|
| 0 | symmetric |
| 1 | symmetric |
| 2 | dual to each other |
| 3 | skew-symmetric |
| 4 | skew-symmetric |
| 5 | skew-symmetric |
| 6 | dual to each other |
| 7 | symmetric |
This appears for instance as (Varadarajan 04, theorem 6.5.7).
Remark
The matrix representation of the bilinear form in prop. is known in the physics literature as the charge conjugation matrix. In matrix calculus the symmetry property means that the transpose matrix satisfies
with given in dimension by the following table
| 0 | -1 |
| 1 | -1 |
| 2 | either |
| 3 | +1 |
| 4 | +1 |
| 5 | +1 |
| 6 | either |
| 7 | -1 |
For instance (van Proeyen 99, table 1).
Over the real numbers (for Majorana spinors)
Proposition
Let be a quadratic vector space, def. over the real numbers of dimension with Loentzian signature. Then there exists, up to rescaling, a unique -invariant bilinear form
on a real irreducible representation of , and its symmetry is given by the following table
| 0 | symmetric |
| 1 | symmetric |
| 2 | dual to each other |
| 3 | skew symmetric |
| 4 | skew symmetric |
| 5 | symmetric |
| 6 | dual to each other |
| 7 | symmetric |
This appears for instance as (Freed 99, around (3.4), Varadarajan 04, theorem 6.5.10).
– super Poincaré bracket (supersymmetry)
We discuss spinor bilinear pairings to vectors.
Over the complex numbers
Proposition
Let be a quadratic vector space, def. over the complex numbers of dimension .
Then there exists unique -representation morphisms
for odd and the unique irreducible representation, and
for even and the two inequivalent irreducible representations.
This is (Varadarajan 04, theorem 6.6.3).
Over the real numbers (for Majorana spinors)
Proposition
Let be a quadratic vector space, def. over the real numbers of dimension .
Then there exists unique -representation morphisms
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
This is (Varadarajan 04, theorem 6.5.10).
For more see (Varadarajan 04, section 6.7).
Pairing to a vector in terms of the charge conjugation matrix
Remark
In terms of a matrix representation with respect to a chosen basis as in remark the pairing of prop. is given by the matrices that represent the Clifford algebra by raising and lowering indices with the charge conjugation matrix of remark (e.g Freed 99 (3.5)).
In such a notation if denotes the component-vector of a spinor, then the result of “lowering its index” is given by acting with the metric in form of the charge conjugation matrix. The result is traditionally denoted
hence
This yields the component formula for the pairings to scalars and to vectors which is traditional in the physics literature as follows:
and
(Recall that all this is here for Majorana spinors, as in the previous prop. .)
This yields the component expressions for the bilinear pairings as familiar from the physics supersymmetry literature, for instance (Polchinski 01, (B.2.1), (B.5.1))
Counting numbers of supersymmetries
A spinor bilinear pairing to a vector as above serves as the odd-odd bracket in a super Poincaré Lie algebra extension of . Since this is also called a “supersymmetry” super Lie algebra, with the spinors being the supersymmetry generators, the decomposition of into minimal/irreducible representations is also called the number of supersymmetries. This is traditionally denoted by a capital and in even dimensions and over the complex numbers it is traditional to write
to indicate that there are copies of the irreducible -representation of one chirality, and of those of the other chirality (i.e. left and right handed Weyl spinors).
This counting however is more subtle over the real numbers (Majorana spinors) and the notation in this case (which happens to be the more important case) is not entirely consistent through the literature.
There is no issue in those dimensions in which the complex Weyl representation already admits a real structure itself, hence when there are Majorana-Weyl spinors. In this case one just counts them with and as in the case over the complex numbers.
However, in some dimensions it is only the direct sum of two Weyl spinor representations which carries a real structure. For instance for and in Lorentzian signature (see the above table) it is the complex representations and , respectively, which carry a real structure. Hence the real representation underlying this parameterizes supersymmetry in terms Majorana spinors, even though its complexification would be . See for instance (Freed 99, p. 53).
Similarly in dimensions 5,6 and 7 mod 8, the minimal real representation is obatained from tensoring the complex spinors with the complex 2-dimensional canonical quaternionic representation (as in the above table). These are also called symplectic Majorana representations. For instance in in 6d one typically speaks of the 6d (2,0)-superconformal QFT to refer to that with a single “symplectic Majorana-Weyl” supersymmetry (e.g. Figueroa-OFarrill, p. 9), which might therefore be counted as real supersymmetric, but which involves two complex irreps and is hence often denoted counted as .
– superconformal bracket
For the moment see at supersymmetry – Superconformal and super anti de Sitter symmetry.
Expression of real representations via real normed division algebras
We discuss a close relation between real spin representations and division algebras, due to Kugo-Townsend 82, Sudbery 84 and others: The real spinor representations in dimensions happen to have a particularly simple expression in terms of Hermitian matrices over the four real normed division algebras: the real numbers themselves, the complex numbers , the quaternions and the octonions . Derived from this also the real spinor representations in dimensions have a fairly simple corresponding expression. We follow the streamlined discussion in Baez-Huerta 09 and Baez-Huerta 10.
Real normed division algebras
To amplify the following pattern and to fix our notation for algebra generators, recall these definitions:
Definition
The complex numbers is the commutative algebra over the real numbers which is generated from one generators subject to the relation
- .
Definition
The quaternions is the associative algebra over the real numbers which is generated from three generators subject to the relations
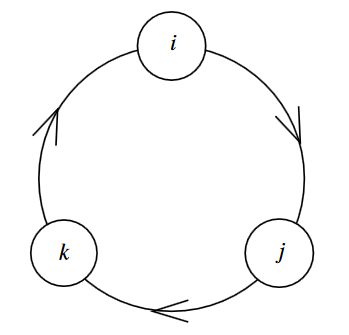
-
for all
-
for a cyclic permutation of then
(graphics grabbed from Baez 02)
Definition
The octonions is the nonassociative algebra over the real numbers which is generated from seven generators subject to the relations
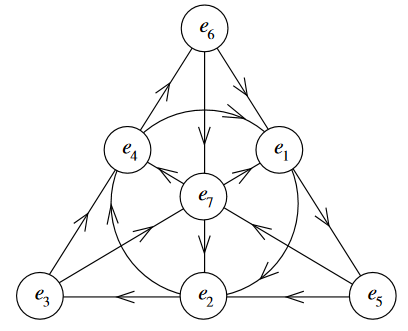
-
for all
-
for an edge or circle in the diagram shown (a labeled version of the Fano plane) then
and all relations obtained by cyclic permutation of the indices in these equations.
(graphics grabbed from Baez 02)
One defines the following operations on these real algebras:
Definition
For , let
be the antihomomorphism of real algebras
given on the generators of def. , def. and def. by
This operation makes into a star algebra. For the complex numbers this is called complex conjugation, and in general we call it conjugation.
Let then
be the function
(“real part”) and
be the function
(“imaginary part”).
It follows that for all then the product of a with its conjugate is in the real center of
and we write the square root of this expression as
called the norm or absolute value function
This norm operation clearly satisfies the following properties (for all )
-
;
-
;
and hence makes a normed algebra.
Since is a division algebra, these relations immediately imply that each is a division algebra, in that
Hence the conjugation operation makes a real normed division algebra.
Remark
Sending each generator in def. , def. and def. to the generator of the same name in the next larger algebra constitutes a sequence of real star-algebra homomorphisms
Proposition
The four algebras of real numbers , complex numbers , quaternions and octonions from def. , def. and def. respectively, which are real normed division algebras via def. , are, up to isomorphism, the only real normed division algebras that exist.
Remark
While hence the sequence from remark
is maximal in the category of real normed non-associative division algebras, there is a pattern that does continue if one disregards the division algebra property. Namely each step in this sequence is given by a construction called forming the Cayley-Dickson double algebra. This continues to an unbounded sequence of real nonassociative star-algebras
where the next algebra is called the sedenions.
What actually matters for the following relation of the real normed division algebras to real spin representations is that they are also alternative algebras:
Definition
Given any non-associative algebra , then the trilinear map
given on any elements by
is called the associator (in analogy with the commutator ).
If the associator is completely antisymmetric (in that for any permutation of three elements then for the signature of the permutation) then is called an alternative algebra.
If the characteristic of the ground field is different from 2, then alternativity is readily seen to be equivalent to the conditions that for all then
We record some basic properties of associators in alternative star-algebras that we need below:
Proposition
Let be an alternative algebra (def. ) which is also a star algebra. Then
-
the associator vanishes when at least one argument is real
-
the associator changes sign when one of its arguments is conjugated
-
the associator vanishes when one of its arguments is the conjugate of another:
-
the associator is purely imaginary
Proof
That the associator vanishes as soon as one argument is real is just the linearity of an algebra product over the ground ring.
Hence in fact
This implies the second statement by linearity. And so follows the third statement by skew-symmetry:
The fourth statement finally follows by this computation:
Here the first equation follows by inspection and using that , the second follows from the first statement above, and the third is the ant-symmetry of the associator.
It is immediate to check that:
Proposition
The real algebras of real numbers, complex numbers, def. ,quaternions def. and octonions def. are alternative algebras (def. ).
Proof
Since the real numbers, complex numbers and quaternions are associative algebras, their associator vanishes identically. It only remains to see that the associator of the octonions is skew-symmetric. By linearity it is sufficient to check this on generators. So let be a circle or a cyclic permutation of an edge in the Fano plane. Then by definition of the octonion multiplication we have
and similarly
The analog of the Hurwitz theorem (prop. ) is now this:
Proposition
The only division algebras over the real numbers which are also alternative algebras (def. ) are the real numbers themselves, the complex numbers, the quaternions and the octonions.
This is due to (Zorn 30).
For the following, the key point of alternative algebras is this equivalent characterization:
Proposition
A nonassociative algebra is alternative, def. , precisely if the subalgebra generated by any two elements is an associative algebra.
This is due to Emil Artin, see for instance (Schafer 95, p. 18).
Proposition is what allows to carry over a minimum of linear algebra also to the octonions such as to yield a representation of the Clifford algebra on . This happens in the proof of prop. below.
So we will be looking at a fragment of linear algebra over these four normed division algebras. To that end, fix the following notation and terminology:
Definition
Let be one of the four real normed division algebras from prop. , hence one of the four real alternative division algebras from prop. .
Say that an matrix with coefficients in , is a hermitian matrix if the transpose matrix equals the componentwise conjugated matrix (def. ):
Hence with the notation
then is a hermitian matrix precisely if
We write for the real vector space of hermitian matrices.
Definition
(trace reversal)
Let be a hermitian matrix as in def. . Its trace reversal is the result of subtracting its trace times the identity matrix:
Spacetime in dimensions 3,4,6 and 10
We discuss how Minkowski spacetime of dimension 3,4,6 and 10 is naturally expressed in terms of the real normed division algebras from prop. , equivalently the real alternative division algebras from prop. .
Proposition
Let be one of the four real normed division algebras from prop. , hence one of the four real alternative division algebras from prop. .
There is a isomorphism (of real inner product spaces) between Minkowski spacetime (def. ) of dimension
hence
-
for ;
-
for ;
-
for ;
-
for .
and the real vector space of hermitian matrices over (def. ) equipped with the inner product whose norm-square is the negative of the determinant operation on matrices:
As a linear map this is given by
Under this identification the operation of trace reversal from def. corresponds to time reversal in that
By direct computation one finds:
Proposition
In terms of the trace reversal operation from def. , the determinant operation on hermitian matrices (def. ) has the following alternative expression
and the Minkowski inner product has the alternative expression
Real spinors in dimensions 3, 4, 6 and 10
We now discuss how real spin representations in dimensions 3,4, 6 and 10 are naturally induced from linear algebra over the four real alternative division algebras.
In particular we establish the following table of exceptional isomorphisms of spin groups:
exceptional spinors and real normed division algebras
Remark
Prop. immediately implies that for then there is a monomorphism from the special linear group (see at SL(2,H) for the definition in the quaternionic case) to the spin group in the given dimension:
given by
This preserves the determinant, and hence the Lorentz form, by the multiplicative property of the determinant:
Hence it remains to show that this is surjective, and to define this action also for being the octonions, where general matrix calculus does not apply, due to non-associativity.
Definition
Let be one of the four real normed division algebras from prop. , hence one of the four real alternative division algebras from prop. .
Define a real linear map
from (the real vector space underlying) Minkowski spacetime to real linear endomorphisms on
Here on the right we are using the isomorphism from prop. for identifying a spacetime vector with a -matrix, and we are using the trace reversal from def. .
Remark
Each operation of in def. is clearly a linear map, even for being the non-associative octonions. The only point to beware of is that for the octonions, then the composition of two such linear maps is not in general given by the usual matrix product.
Proposition
The map in def. gives a representation of the Clifford algebra , i.e of
-
for ;
-
for ;
-
for ;
-
for .
Hence this Clifford representation induces representations of the spin group on the real vector spaces
Proof
We need to check that the Clifford relation
is satisfied. Now by definition, for any then
where on the right we have in each component ordinary matrix product expressions.
Now observe that both expressions on the right are sums of triple products that involve either one real factor or two factors that are conjugate to each other:
Since the associators of triple products that involve a real factor and those involving both an element and its conjugate vanish by prop. (hence ultimately by Artin’s theorem, prop. ), in conclusion all associators involved vanish, so that we may rebracket to obtain
Remark
Prop. says that the isomorphism of prop. is that given by forming generalized Pauli matrices. In standard physics notation these matrices are written as
Proposition
The spin representations given via prop. by the Clifford representation of def. are the following:
-
for the Majorana representation of on ;
-
for the Majorana representation of on ;
-
for the Weyl representation of on and on ;
-
for the Majorana-Weyl representation of on and on .
Proposition
Under the identification of prop. the bilinear pairings
and
from above are given, respectively, by forming the real part of the canonical -inner product
and by forming the product of a column vector with a row vector to produce a matrix, possibly up to trace reversal (def. ):
and
For the -component of this map is
(Baez-Huerta 09, prop. 8, prop. 9).
Example
Consider the case of real numbers.
Now is the space of symmetric 2x2-matrices with real numbers.
The “light-cone”-basis for this space would be
Hence the Minkowski metric of prop. in this basis has the components
As vector spaces .
The bilinear spinor pairing is given by
The spinor pairing from prop. is given on an () by the components
and is given by the components
and so, in view of the above metric components, in terms of dual bases this is
So there is in particular the 2-dimensional space of isomorphisms of super Minkowski spacetime super translation Lie algebras
(not though of the corresponding super Poincaré Lie algebras, because for them the difference in the Spin-representation does matter) spanned by
and by
Hence there is a 1-dimensional space of non-trivial automorphism
spanned by
Real spinors in dimensions 4,5,7 and 11
Remark
The real vector space in def. equipped with the inner product given by
-
for ;
-
for ;
-
for ;
-
for .
Proposition
The map in def. gives a representation of the Clifford algebra of
-
for ;
-
for ;
-
for ;
-
for .
Under restriction along this is isomorphic to
-
for the Majorana representation of on ;
-
for the Dirac representation of on ;
-
for the Dirac representation of on ;
-
for the Majorana representation of on .
(Baez-Huerta 10, p. 10, prop. 8, prop. 9)
Write
Proposition
Under the identification of prop. of the bilinear pairings
and
of remark , the first is given by
and the second is characterized by
(Baez-Huerta 10, prop. 10, prop. 11).
Related entries
References
Accounts in the physics literature include:
- Leonardo Castellani, Riccardo D'Auria, Pietro Fré, Ch II.7 in: Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991) [doi:10.1142/0224, toc: pdf, chII.7: pdf]
Accounts in the mathematical literature include
-
H. Blaine Lawson, Marie-Louise Michelsohn, Chapter I.5 of Spin geometry, Princeton University Press (1989)
-
Anna Engels, Spin representations (pdf)
Specifically for Lorentzian signature and with an eye towards supersymmetry in QFT, see
-
Daniel Freed, Lecture 3 of Five lectures on supersymmetry 1999
-
Veeravalli Varadarajan, section 7 of Supersymmetry for mathematicians: An introduction, Courant lecture notes in mathematics, American Mathematical Society, Providence, R.I (2004)
With an eye towards application in grand unified theory:
- Howard Georgi, §21 & 22 in: Lie Algebras In Particle Physics, Westview Press (1999), CRC Press (2019) [doi:10.1201/9780429499210]
For the component notation traditionally used in physics see for instance
-
Antoine Van Proeyen, Tools for supersymmetry, Lectures in the spring school in Calimanesti, Romania, April 1998 (arXiv:hep-th/9910030)
-
Joseph Polchinski, part II, appendix B of String theory, Cambridge Monographs on Mathematical Physics (2001)
-
Friedemann Brandt, section 2 of Supersymmetry algebra cohomology I: Definition and general structure J. Math. Phys.51:122302, 2010, (arXiv:0911.2118)
For good math/physics discussion with special emphasis on the symplectic Majorana spinors and their role in the 6d (2,0)-superconformal QFT see
- José Figueroa-O'Farrill, Majorana spinors [pdf, pdf]
A clean summary of the relation of the real representation to Hermitian forms over the real normed division algebras is in
-
John Baez, John Huerta, Division algebras and supersymmetry I, in R. Doran, G. Friedman and Jonathan Rosenberg (eds.), Superstrings, Geometry, Topology, and -algebras, Proc. Symp. Pure Math. 81, AMS, Providence, 2010, pp. 65-80 (arXiv:0909.0551)
-
John Baez, John Huerta, Division algebras and supersymmetry II, Adv. Math. Theor. Phys. 15 (2011), 1373-1410 (arXiv:1003.34360)
Last revised on August 8, 2025 at 15:27:30. See the history of this page for a list of all contributions to it.