nLab rotation gate
Context
Quantum systems
-
quantum algorithms:
Contents
Idea
In quantum information theory and quantum computing, by a rotation gate one means a quantum gate acting on a single qbit — regarded as a spinor acted on by SU(2) Spin(3) — by rotation of any given angle around one of the coordinate 3 axes.
Concretely, the standard notational convention for these gates in the canonical qbit measurement basis is the following (where , , denote the Pauli gates and is the rotation angle):
Remark
To appreciate the -domain of the angle variable , recall that the action of these linear operators on is rotation of spinors, double-covering rotation of vectors which instead is given by the conjugation action:
In particular, in each case becomes the identity operation (only) under the spin double cover map .
Applications
Quantum Fourier transform
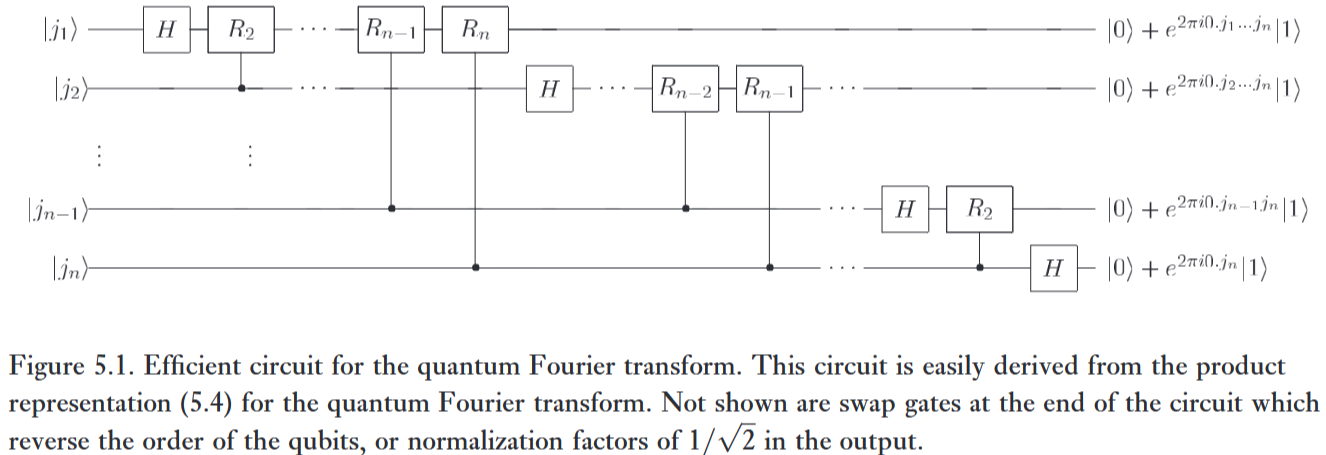
Controlled rotation gates play a key role in the quantum Fourier transform (and thus in many quantum algorithms, notably in Shor's algorithm).
Concretely, quantum circuits implementing the quantum Fourier transform employ many copies [Nielsen & Chuang 2000 (5.11) & Fig. 5.1, pp 218] of the gates
for .
Related gates
References
Textbook account:
- Michael A. Nielsen, Isaac L. Chuang, (4.4-6) in: Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]
In Shor's algorithm:
- Austin G. Fowler, Lloyd C. L. Hollenberg: Scalability of Shor’s algorithm with a limited set of rotation gates, Phys. Rev. A 70 (2004) 032329 [arXiv:quant-ph/0306018, doi:10.1103/PhysRevA.70.032329]
Last revised on February 15, 2025 at 16:52:58. See the history of this page for a list of all contributions to it.