Schreiber What is... the nLab

$\;\;\;\;\;\;$ A wiki lab notebook for reference and research notes in mathematics and physics.

(Urs Schreiber, presentation at “Big Data in Pure Math 2022”)

---

Denis Diderot on the need for his Encyclopédie (in 1750, see here):

As long as the centuries continue to unfold, the number of books will grow continually, and one can predict that a time will come when it will be almost as difficult to learn anything from books as from the direct study of the whole universe. It will be almost as convenient to search for some bit of truth concealed in nature as it will be to find it hidden away in an immense multitude of bound volumes. When that time comes, a project, until then neglected because the need for it was not felt, will have to be undertaken.

Thanks to encyclopedic ordering, the universality of knowledge, and the frequency of references, the connections grow, the links go out in all directions, the demonstrative power is increased, the word list is complemented, fields of knowledge are drawn closer together and strengthened; we perceive either the continuity or the gaps in our system, its weak sides, its strong points, and at a glance on which objects it is important to work for one’s own glory, or for the greater utility to humankind. If our dictionary is good, how many still better works it will produce.

Michael Polanyi in Personal Knowledge (1958):

The transmission of mathematics has today been rendered more precarious than ever by the fact that no single mathematician can fully understand any longer more than a tiny fraction of mathematics. Modern mathematics can be kept alive only by a large number of mathematicians cultivating different parts of the same system of values: a community which can be kept coherent only by the passionate vigilance of universities, journals and meetings, fostering these values and imposing the same respect for them on all mathematicians. Such a far-flung structure is highly vulnerable and, once broken, impossible to restore. Its ruins would bury modern mathematics in an oblivion more complete and lasting than that which enveloped Greek mathematics twenty-two centuries ago.” (1958: 192-3)

---

fundamental nLab features:

• simple markup for easy page formatting

• basic LaTeX-like math typesetting

• hyperlinking

• hyperlinking

• hyperlinking

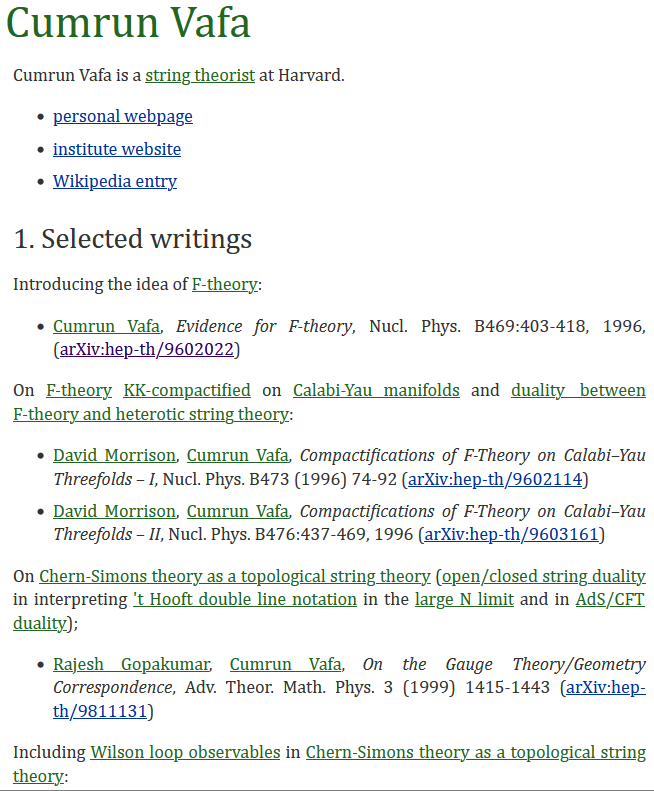
on the right a typical nLab page $\;\;\rightarrow$

below its source code

$\downarrow$

---

the nLab is:

• more research-level than Wikipedia, but also

• more freewheeling than Stacks project or Kerodon

strong encyclopedic component,

• but this is a side effect, not the core motivation

some swarm component, “enough eyeballs”-effect

• readers fix mistakes, make improvements, …

large range of types of pages:

• some monograph-size pages, eg.

  • geometry of physics – categories and toposes

  • Introduction to Stable Homotopy Theory

• many single-definition pages, eg.

  • sylleptic 3-group

  • ring of Witt vectors

• and all kinds of stuff in-between:

  • lecture notes:

    fundamental super p-branes, …

  • online book indices:

    Sketches of an Elephant, Higher Topos Theory, …

  • living reviews:

    AdS-QCD correspondence, …

  • conference proceedings:

    New Spaces for Mathematics and Physics,

    M-Theory and Mathematics, …

  • research group activities:

    Center for Quantum and Topological Systems, …

  • updates on physics experiments:

    flavour anomaly, …

  • intellectual exotica:

    Science of Logic, universal exceptionalism, …

---

large range of topics:

… topos theory $\;\;\;$ hadrodynamics $\;\;\;$ Weil conjectures $\;\;\;$ differential geometry $\;\;\;$ D-branes $\;\;\;$ foundations of mathematics $\;\;\;$ type theory $\;\;\;$ algebraic geometry $\;\;\;$ string theory $\;\;\;$ Stone duality $\;\;\;$ constructivism $\;\;\;$ intersecting branes $\;\;\;$ $(\infty,1)$-category theory $\;\;\;$ flavour physics $\;\;\;$ AdS/CFT $\;\;\;$ AdS/QCD $\;\;\;$ AdS/CMT $\;\;\;$ functorial geometry $\;\;\;$ Goodwillie calculus $\;\;\;$ calculus $\;\;\;$ synthetic differential geometry $\;\;\;$ orbifold $\;\;\;$ orientifold $\;\;\;$ Poincaré conjecture $\;\;\;$ higher structures $\;\;\;$ higher geometry $\;\;\;$ proton $\;\;\;$ $\;\;\;$ higher algebra $\;\;\;$ higher differential geometry $\;\;\;$ geometry of physics $\;\;\;$ super Lie algebra $\;\;\;$ chord diagram $\;\;\;$ computability $\;\;\;$ intuitionistic mathematics $\;\;\;$ Lie algebroid $\;\;\;$ mass gap problem $\;\;\;$ confinement $\;\;\;$ K-theory classification of D-brane charge $\;\;\;$ K-theory classification of topological phases of matter $\;\;\;$ quark $\;\;\;$ graphene $\;\;\;$ (0,1)-category $\;\;\;$ order theory $\;\;\;$ Hamiltonian $\;\;\;$ quantum physics $\;\;\;$ collapse of the wavefunction $\;\;\;$ commutativity of limits and colimits $\;\;\;$ categorical semantics $\;\;\;$ M-theory $\;\;\;$ relation between category theory and type theory $\;\;\;$ homotopy type theory $\;\;\;$ category theory $\;\;\;$ non-perturbative effect $\;\;\;$ cohesive $(\infty,1)$-topos $\;\;\;$ operad $\;\;\;$ monad $\;\;\;$ Beck-Chevalley condition $\;\;\;$ proof assistant $\;\;\;$ WZW model $\;\;\;$ conformal block $\;\;\;$ Knizhnik-Zamolodchikov equation $\;\;\;$ configuration space of points $\;\;\;$ cohomology $\;\;\;$ homotopy $\;\;\;$ cohomotopy $\;\;\;$ generalized cohomology $\;\;\;$ stable splitting of mapping spaces $\;\;\;$ equivariant homotopy theory $\;\;\;$ symmetric spectra $\;\;\;$ convenient category of topological spaces $\;\;\;$ point-set topology $\;\;\;$ decidability $\;\;\;$ adjoint functor theorem $\;\;\;$ infinitesimals $\;\;\;$ space form $\;\;\;$ supergeometry $\;\;\;$ superalgebra $\;\;\;$ exceptional isomorphism $\;\;\;$ universal exceptionalism $\;\;\;$ tachyon $\;\;\;$ RR-field $\;\;\;$ K-theory $\;\;\;$ elliptic cohomology $\;\;\;$ TMF $\;\;\;$ Morava K-theory $\;\;\;$ redshift conjecture $\;\;\;$ rational homotopy theory $\;\;\;$ differential cohomology $\;\;\;$ group of ideles $\;\;\;$ paradox $\;\;\;$ axiom of choice $\;\;\;$ set theory $\;\;\;$ Euler-Lagrange equations $\;\;\;$ jet comonad $\;\;\;$ partial differential equation $\;\;\;$ motive $\;\;\;$ deformation quantization $\;\;\;$ geometric quantization $\;\;\;$ topological quantum field theory $\;\;\;$ cobordism category $\;\;\;$ cobordism hypothesis $\;\;\;$ cobordism cohomology $\;\;\;$ Witt vector $\;\;\;$ absolute geometry $\;\;\;$ Spec(Z) $\;\;\;$ internalization $\;\;\;$ enriched category theory $\;\;\;$ Burnside ring $\;\;\;$ Chern character $\;\;\;$ twisted de Rham cohomology $\;\;\;$ flavour anomaly $\;\;\;$ inhomogeneous cosmology $\;\;\;$ Bohr topos $\;\;\;$ quantum probability $\;\;\;$ perturbative quantum field theory $\;\;\;$ Feynman diagram $\;\;\;$ renormalization $\;\;\;$ worldline formalism $\;\;\;$ group actions on spheres $\;\;\;$ spherical space form $\;\;\;$ GAGA principle $\;\;\;$ structure sheaf $\;\;\;$ …

---

towards the original vision of hypertext:

every technical term is hyperlinked (ideally):

---

this allows fully hyperlinked

and contextualized referencing:

on the right a typical author-bib page

---

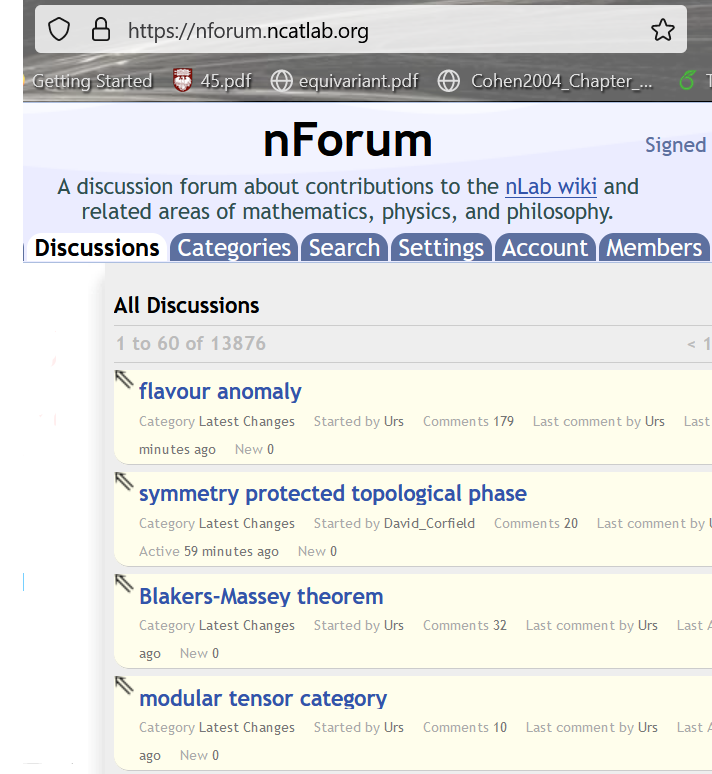
discussion / page talk on the nForum

---

The active user base is small,

wiki has grown slowly – but steadily.

Recently more activity from HoTT community

General observation:

The more formalized a field

the easier its members find it to contribute

Eternal hope: To help break this pattern.

---

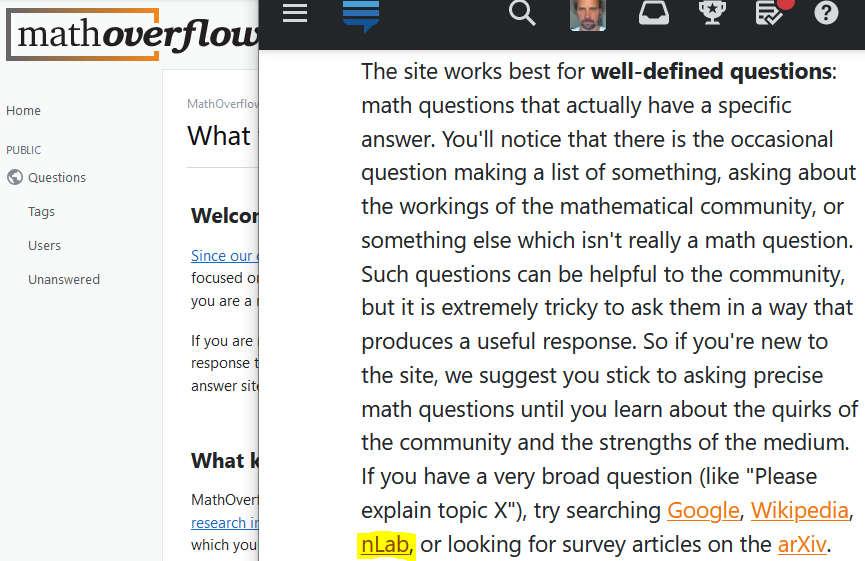
Here is how MathOverflow is pointing users to the nLab:

---

Here is PhysicsOverflow

linking to the nLab for reference

---

Here is the Quanta Magazine

linking to the nLab for background

---

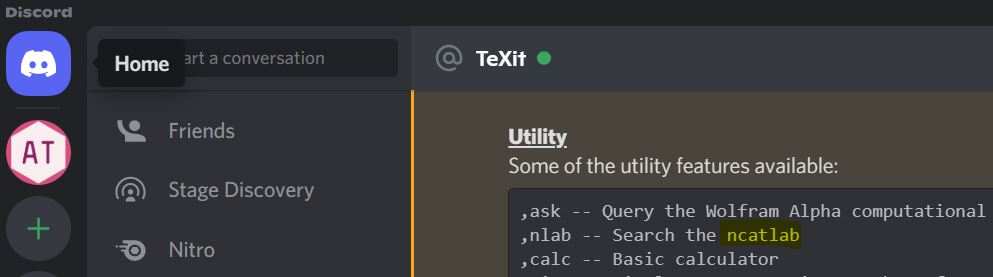
Here is the Algebraic Topology Discord

pointing to the nLab for general reference

---

something akin to the nLab wiki has now

been started in Chinese: bananaspace

(name is inside joke on Banach space)

---

what the nLab is to me:

online research assistant

I make essentially all my notes during research on the nLab:

when I dig out any reference, I go record it with commentary on the nLab,

if the relevant page does not exist yet, I start a stub entry on the topic

if a lemma, proof or fact was hard to find but seems noteworthy, I make a note

if there is an unexpected cross-relation to another topic, I put a hyperlink,

once I have a good idea of a new subject, I give the entry an Idea-section,

and so on.

Thus when done with a new article, essentially all its concepts have nLab articles.

---

For instance, this allows me to have completely hyperlinked abstracts, e.g.:

---

various publications arose from nLab-discussion:

---

blessing and curse of Category Theory

category theory is meant as backdrop not as focus

helps to organize and unify the vast scope of topics

but nLab-contributions need not be categorical at all

on the contrary, a thorough supply of traditional material

is the substrate on which the nPOV comes into action

a better name for nLab might have been MathPhys-Lab.

---

if you want to join in: welcome!

best to warm up with small edits first

just go to any page and hit edit at the bottom:

best to try out edits in the Sandbox

all other entries will ask you for a brief edit log:

this will appear in a thread on the nForum

further exchange/discussion: on the nForum

this is where we talk: see you at the nForum!

---

---

Acknowledgements.

The nLab logo was created by David Roberts.

The lead-in quotes are thanks to David Corfield.

In general:

Thanks to all nLab contributors!

Thanks to everyone who supports the nLab with donations!

Thanks to the technical board for keeping the server running!

Last not least, thanks to Steve Awodey for sponsoring the server!

---