nLab black holes in string theory

Black hole entropy

In (perturbative) string theory the Bekenstein-Hawking entropy associated to a macroscopic black hole finds an explanation as follows:

The black hole spacetime is regarded as a strongly coupled condensate of string states (closed strings, carrying gravity). One looks for a corresponding weakly-coupled background for closed strings in flat Minkowski space that is known to turn into the black hole spacetime as the string coupling is turned on. Such turn out to be certain D-brane configurations in Minkowski space: at weak coupling the D-brane does not back-react on the spacetime (since that back-reaction is mediated by closed string quanta) and so it just sits there, whereas at strong coupling it curves spacetime and may collapse to a configuration that looks like the prescribed black hole spacetime.

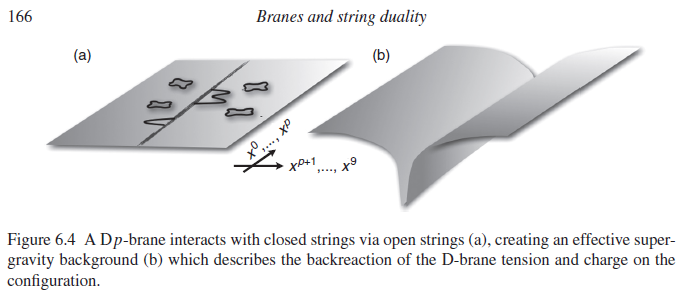
graphics grabbed from Ibanez-Uranga 12

Now, if the configuration has a sufficient amount of supersymmetry preserved (BPS state), then one argues (Witten 95, section 2.3) that certain observables are actually independent of the coupling constant (“protection from quantum corrections”), and accordingly these observables are the same for black holes as for the corresponding D-brane configurations in flat space, where they may be computed in string perturbation theory.

The best studied such configuration is that of D1-D5 brane bound states. For these configurations one may compute the number of BPS states (which are “protected”), hence the entropy, via the Witten genus (Strominger-Vafa 96), see at Witten genus – Relation to BPS state counting. By the above reasoning this may then be compared to the Bekenstein-Hawking entropy of the corresponding (supersymmetric) black hole. And indeed the results match the semiclassical BH-entropy to leading order and in addition provide their higher order quantum corrections. See the References below.

The T-dual version of the D1/D5-bound states are D0/D6-bound states, coming from the Kaluza-Klein monopole in 11-dimensional supergravity (e.g. Nelson 93).

Related concepts

• extremal black hole

• black ring

• black brane

  • black hole

  • black string

  • black membrane?

  • black fivebrane

• AdS/CFT correspondence

  • Sachdev-Ye-Kitaev model

• gravitational entropy

  • Bekenstein-Hawking entropy

  • generalized second law of thermodynamics

  • black holes in string theory

  • holographic entanglement entropy

Table of branes appearing in supergravity/string theory (for classification see at brane scan).

brane	in supergravity	charged under gauge field	has worldvolume theory
black brane	supergravity	higher gauge field	SCFT
D-brane	type II	RR-field	super Yang-Mills theory
$(D = 2n)$	type IIA	$\,$	$\,$
D(-2)-brane	$\,$	$\,$
D0-brane	$\,$	$\,$	BFSS matrix model
D2-brane	$\,$	$\,$	$\,$
D4-brane	$\,$	$\,$	D=5 super Yang-Mills theory with Khovanov homology observables
D6-brane	$\,$	$\,$	D=7 super Yang-Mills theory
D8-brane	$\,$	$\,$
$(D = 2n+1)$	type IIB	$\,$	$\,$
D(-1)-brane	$\,$	$\,$	$\,$
D1-brane	$\,$	$\,$	2d CFT with BH entropy
D3-brane	$\,$	$\,$	N=4 D=4 super Yang-Mills theory
D5-brane	$\,$	$\,$	$\,$
D7-brane	$\,$	$\,$	$\,$
D9-brane	$\,$	$\,$	$\,$
(p,q)-string	$\,$	$\,$	$\,$
(D25-brane)	(bosonic string theory)
NS-brane	type I, II, heterotic	circle n-connection	$\,$
string	$\,$	B2-field	2d SCFT
NS5-brane	$\,$	B6-field	little string theory
D-brane for topological string			$\,$
A-brane			$\,$
B-brane			$\,$
M-brane	11D SuGra/M-theory	circle n-connection	$\,$
M2-brane	$\,$	C3-field	ABJM theory, BLG model
M5-brane	$\,$	C6-field	6d (2,0)-superconformal QFT
M9-brane/O9-plane			heterotic string theory
M-wave
topological M2-brane	topological M-theory	C3-field on G₂-manifold
topological M5-brane	$\,$	C6-field on G₂-manifold
S-brane
SM2-brane, membrane instanton
M5-brane instanton
D3-brane instanton
solitons on M5-brane	6d (2,0)-superconformal QFT
self-dual string		self-dual B-field
3-brane in 6d

• 5d supergravity

References

A careful non-technical exposition is in

• Sebastian De Haro, Jeroen van Dongen, Manus Visser, Jeremy Butterfield, Conceptual Analysis of Black Hole Entropy in String Theory (arXiv:1904.03232)

• Jeroen van Dongen, Sebastian De Haro, Manus Visser, Jeremy Butterfield, Emergence and Correspondence for String Theory Black Holes (arXiv:1904.03234)

Introductions and Review

• Juan Maldacena, Black Holes in String Theory, PhD thesis 1996 (arXiv:hep-th/9607235)

• Juan Maldacena, Black Holes and D-branes, Nucl. Phys. Proc. Suppl. 61A (1998) 111-123; Nucl. Phys. Proc. Suppl. 62 (1998) 428-442 (arXiv:hep-th/9705078)

• Mike Duff, chapter 5 of The World in Eleven Dimensions: Supgergravity, Supermembranes and M-theory, IoP 1999 (publisher)

• Kostas Skenderis, Black holes and branes in string theory, Lect.Notes Phys. 541 (2000) 325-364 (arXiv:hep-th/9901050)

• Thomas Mohaupt, Black Hole Entropy, Special Geometry and Strings, Fortsch.Phys. 49 (2001) 3-161 (arXiv:hep-th/0007195)

• Sumit R. Das, Samir Mathur, The Quantum Physics of Black Holes: Results from String Theory (arXiv:gr-qc/0105063)

• Justin R. David, Gautam Mandal, Spenta R. Wadia, Microscopic Formulation of Black Holes in String Theory (arXiv:hep-th/0203048)

• Thibault Damour, The entropy of black holes: a primer (arXiv:hep-th/0401160)

• Barton Zwiebach, chapter 22 of A first course in string theory

• Per Kraus, Lectures on black holes and the $AdS_3/CFT_2$ correspondence, Lect. Notes Phys.755:193-247, 2008 (arXiv:hep-th/0609074)

  Stringy black holes in five dimensions, 2007 (pdf slides)

• Xi Yin, Black Holes, Anti de Sitter space, and Topological Strings, 2006 (pdf)

• Ashoke Sen, Black Hole Entropy Function, Attractors and Precision Counting of Microstates, Gen. Rel. Grav. 40: 2249-2431, 2008 (arXiv:0708.1270)

• Joao Gomes, Quantum entropy of supersymmetric black holes (arXiv:1111.2025)

• Luis Ibáñez, Angel Uranga, section 6.2 of String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012

• Dieter Lüst, Ward Vleeshouwers, Black Hole Information and Thermodynamics (arXiv:1809.01403)

• Alberto Zaffaroni, Lectures on AdS Black Holes, Holography and Localization (arXiv:1902.07176)

• Lorenzo Pieri, Black Holes in String Theory (arXiv:1911.11670)

Lectures on AdS Black Holes, Holography and Localization Alberto Zaffaroniee also

• String Theory Wiki, Black hole entropy

Original articles

The argument that properties of BPS states are preserved as the coupling increases beyond perturbation theory and are not destroyed by non-perturbative effects originates in

• Edward Witten, section 2.3 of String Theory Dynamics In Various Dimensions, Nucl.Phys.B443:85-126,1995 (arXiv:hep-th/9503124)

The original computations of stringy black hole entropy using this argument are due to

• Ashoke Sen, Extremal black holes and elementary string states, Mod. Phys. Lett. A10: 2081-2094, 1995 (arXiv:hep-th/9504147)

• Andrew Strominger, Cumrun Vafa, Microscopic Origin of the Bekenstein-Hawking Entropy, Phys. Lett. B379: 99-104, 1996 (arXiv:hep-th/9601029)

• Curtis Callan, Juan Maldacena, D-brane Approach to Black Hole Quantum Mechanics, Nucl. Phys. B472:591-610, 1996 (arXiv:hep-th/9602043)

• Juan Maldacena, Gregory Moore, Andrew Strominger, Counting BPS Blackholes in Toroidal Type II String Theory (arXiv:hep-th/9903163)

• Davide Gaiotto, Andrew Strominger, X. Yin, New Connections Between 4D and 5D Black Holes, JHEP 0602:024,2006 (arXiv:hep-th/0503217)

See also

• Emil Martinec, V. Sahakian, Black Holes and Five-brane Thermodynamics, Phys.Rev. D60 (1999) 064002 (arXiv:hep-th/9901135)

Discussion for M-theory/11-dimensional supergravity includes

• Juan Maldacena, Andrew Strominger, Edward Witten, Black Hole Entropy in M-Theory, JHEP 9712:002,1997 (arXiv:hep-th/9711053)

• Gary Horowitz , M. Roberts, Counting the microstates of a Kerr black hole in M theory, Phys Rev Lett. 2007 Nov 30;99(22):221601. Epub 2007 Nov 30. (web), (arXiv:0708.1346)

• Davide Gaiotto, Andrew Strominger, Xi Yin, The M5-Brane Elliptic Genus: Modularity and BPS States, JHEP 0708:070,2007 (arXiv:hep-th/0607010)

Discussion relating to the Kaluza-Klein monopole includes

• William Nelson, Kaluza-Klein Black Holes in String Theory, Phys.Rev.D49:5302-5306,1994 (arXiv:hep-th/9312058)

More recent developments include

• Alejandra Castro, Joshua L. Davis, Per Kraus, Finn Larsen, String Theory Effects on Five-Dimensional Black Hole Physics (arXiv:0801.1863)

• Oleg Lunin, Samir Mathur, A toy black hole S-matrix in the D1-D5 CFT (arXiv:1211.5830)

• Alejandra Castro, Joshua M. Lapan, Alexander Maloney, Maria J. Rodriguez, Black Hole Monodromy and Conformal Field Theory (arXiv:1303.0759)

• H. L. Dao, Parinya Karndumri, Supersymmetric $AdS_5$ black holes and strings from 5D $N=4$ gauged supergravity (arXiv:1812.10122)

• Behnam Pourhassan, Mubasher Jamil, Mir Faizal, Black Remnants from T-Duality (arXiv:1912.09235)

See also:

• Nejc Čeplak, Roberto Emparan, Andrea Puhm, Marija Tomašević, The correspondence between rotating black holes and fundamental strings, JHEP 11 (2023) 226 [arXiv:2307.03573, doi:10.1007/JHEP11(2023)226]

BPS black holes in $AdS_5/CFT_4$ duality

(…)

• Alejandro Cabo-Bizet, Davide Cassani, Dario Martelli, Sameer Murthy, Microscopic origin of the Bekenstein-Hawking entropy of supersymmetric $AdS_5$ black holes (arXiv:1810.11442)

• Sunjin Choi, Joonho Kim, Seok Kim, June Nahmgoong, Large AdS black holes from QFT (arxiv:1810.12067)

• Francesco Benini, Paolo Milan, Black holes in 4d $\mathcal{N} = 4$ Super-Yang-Mills (arXiv:1812.09613)

(…)

The D$p$-brane bound states

• Konstadinos Sfetsos, Kostas Skenderis, Microscopic derivation of the Bekenstein-Hawking entropy formula for non-extremal black holes, Nucl. Phys. B517 (1998) 179-204 (arXiv:hep-th/9711138)

• Mohammad R. Garousi, Ahmad Ghodsi, Entropy Function for Non-extremal D1D5 and D2D6NS5-branes, JHEP 0710:036, 2007 (arXiv:0705.2149)

D1-D5 brane systems

Discussion of black hole entropy via D1-D5 brane bound states as black holes in string theory:

(…) many references go here (…)

• Emil Martinec, The branes behind black holes, talk at Strings 2022 [indico:4940814]

D2-D6-NS5 brane systems

Discussion of black hole entropy of D2-D6 brane bound states as black holes in string theory:

• Juan Maldacena, Andrew Strominger, Statistical Entropy of Four-Dimensional Extremal Black Holes, Phys. Rev. Lett. 77:428-429, 1996 (arXiv:hep-th/9603060)

Black holes in supergravity

Black holes in supergravity:

• Riccardo D'Auria, Pietro Fre, BPS black holes in supergravity, (hep-th/9812160)

• Antonio Gallerati, Constructing black hole solutions in supergravity theories (arXiv:1905.04104)

Resolution of scalar field-dressed Schwarzschild black holes in D=11 supergravity:

• Ibrahima Bah, Pierre Heidmann, Geometric Resolution of Schwarzschild Horizon [arXiv:2303.10186]

Fat black holes

Discussion of black holes whose Schwarzschild radius is larger than the KK-compactification-scale:

• Juan Maldacena, Leonard Susskind, D-branes and Fat Black Holes, Nucl. Phys.B475:679-690 (1996) (arXiv:hep-th/9604042)

• E. Halyo, Arvind Rajaraman, Leonard Susskind, Braneless Black Holes, Phys. Lett.B392:319-322 (1997) (arXiv:hep-th/9605112)

• A.A. Bytsenko, S.D. Odintsov, p. 8 of: Statistical entropy of near-extremal and fundamental black p-branes, Prog. Theor. Phys. 98:987-1003 (1997) (arXiv:hep-th/9611151)

Discussion in BFSS matrix theory

Discussion of black holes via the BFSS matrix model includes the following:

• Tom Banks, Willy Fischler, Igor Klebanov, Leonard Susskind, Schwarzschild Black Holes from Matrix Theory, Phys.Rev.Lett.80:226-229,1998 (arXiv:hep-th/9709091)

• Tom Banks, Willy Fischler, Igor Klebanov, Leonard Susskind, Schwarzchild Black Holes in Matrix Theory II, JHEP 9801:008,1998 (arXiv:hep-th/9711005)

• Igor Klebanov, Leonard Susskind, Schwarzschild Black Holes in Various Dimensions from Matrix Theory, Phys.Lett.B416:62-66,1998 (arXiv:hep-th/9709108)

• Edi Halyo, Six Dimensional Schwarzschild Black Holes in M(atrix) Theory (arXiv:hep-th/9709225)

• Gary Horowitz, Emil Martinec, Comments on Black Holes in Matrix Theory, Phys. Rev. D 57, 4935 (1998) (arXiv:hep-th/9710217)

• Daniel Kabat, Washington Taylor, Spherical membranes in Matrix theory, Adv.Theor.Math.Phys.2:181-206,1998 (arXiv:hep-th/9711078)

• Yoshifumi Hyakutake, Black Hole and Fuzzy Objects in BFSS Matrix Model (arXiv:1801.07869)

Relation to topological string amplitudes

Discussion of black hole microstates via the topological string‘s Gopakumar-Vafa invariants:

• Rajesh Gopakumar, Cumrun Vafa, M-Theory and Topological Strings–I (arXiv:hep-th/9809187, bibcode:1998hep.th….9187G)

• Rajesh Gopakumar, Cumrun Vafa, M-Theory and Topological Strings–II (arXiv:hep-th/9812127, bibcode:1998hep.th…12127G)