nLab heterotic M-theory on ADE-orbifolds

Idea

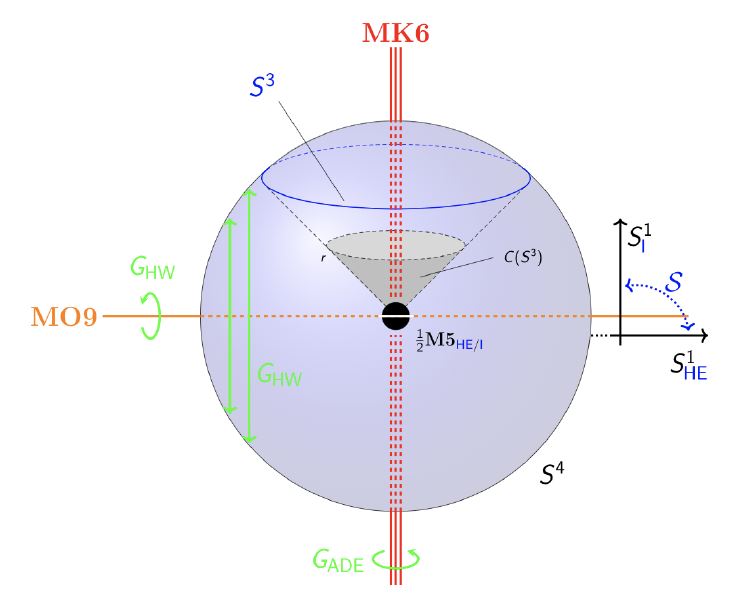
The KK-compactification of M-theory on fibers

$$S^1 \!\sslash\! G_{HW} \times \mathbb{H}\!\sslash\! G_{ADE}$$

which are, locally, the Cartesian product of

1. the circle orientifolded by $G_{HW} \simeq \mathbb{Z}_2$ as in Horava-Witten theory;

2. the quaternions orbifolded by a finite subgroup of SU(2) $G_{ADE}$.

(Sen 97, Sec 3, Faux-Lüst-Ovrut 99, Kaplunovsky-Sonnenschein-Theisen-Yankielowicz 99, Faux-Lüst-Ovrut 00a, 00b, 00c)

graphics grabbed from HSS18, Example 2.2.7

For $G_{ADE} = \mathbb{Z}_2$ this subsumes M-theory on K3 times $S^1 \sslash G_{HW}$ (Seiberg-Witten 96)

Dual string theory perspectives

Under duality in string theory (specifically: duality between M-theory and type IIA string theory and duality between M-theory and heterotic string theory) M-theory on $\mathbb{S}^{1}\sslash \mathbb{Z}_2^{HW} \times \mathbb{T}^{4}\sslash G^{ADE}$ appears through the following string theory-perspectives

1. $HET_{E}$-Theory on ADE-singularities

2. $I'$-Theory with D6-branes on O8-planes

3. $I'$-Theory on ADE-singularities intersecting O8-planes

The following graphics shows how the three perspectives arise from KK-compactification on three different choices of circle-fibers. Indicated also are the M5-branes and their string theoretic images at NS5-branes/D4-branes with geometrically engineer D=6 N=(1,0) SCFTs (see further below).

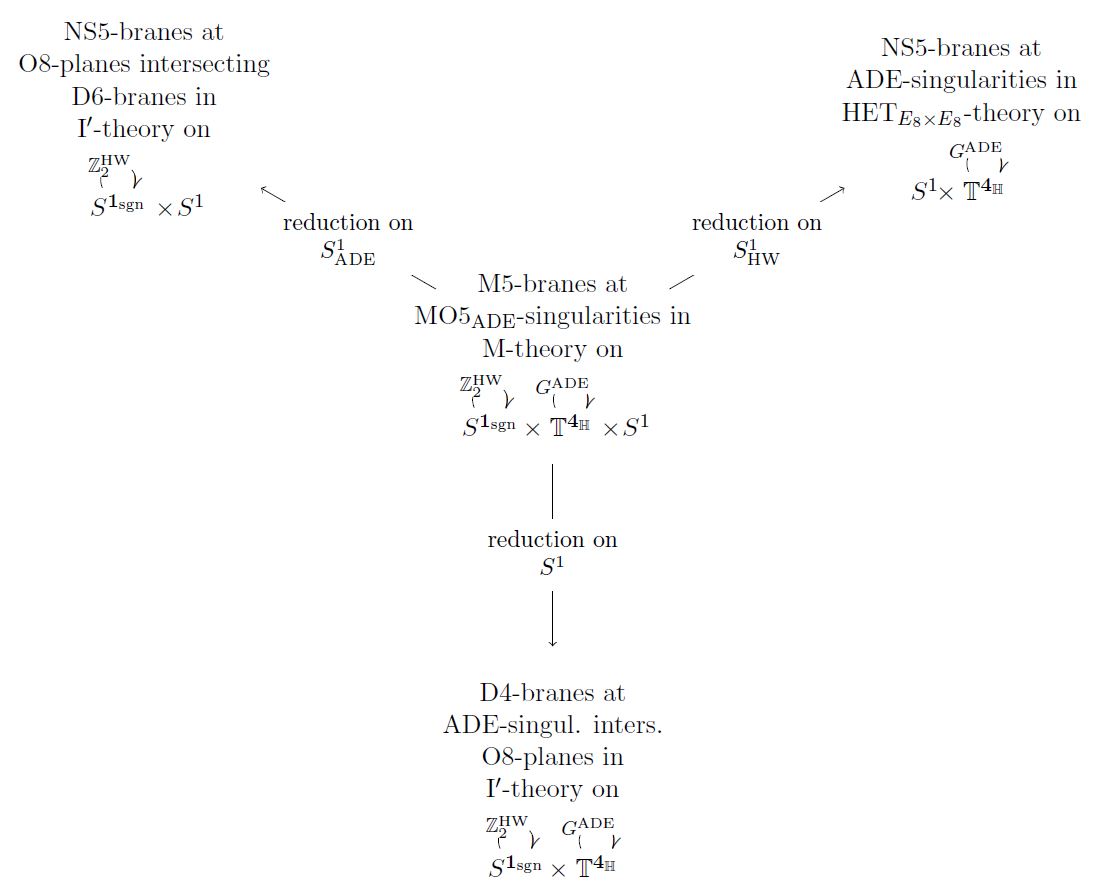
graphics grabbed from SS19

$HET_{E}$-Theory on ADE-singularities

(…)

Horava-Witten theory, hence heterotic string theory, on ADE-singularities $\mathbb{H} \sslash G_{ADE}$

(Witten 99,…)

(…)

$I'$-Theory with D6-branes on O8-planes

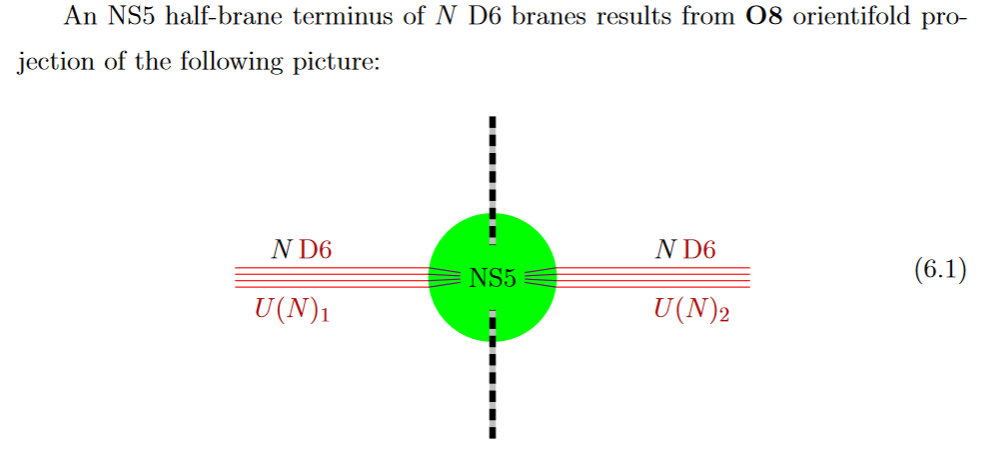
from GKSTY 02

If in addition the black NS5-brane sits at an O8-plane, hence at the orientifold fixed point-locus, then in the ordinary $\mathbb{Z}/2$-quotient it appears as a “half-brane” – the half M5-brane – with only one copy of D6-branes ending on it:

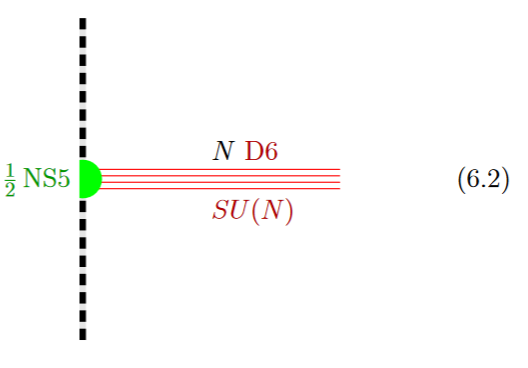
graphics grabbed from GKSTY 02

(In Hanany-Zaffaroni 99 this is interpreted in terms of the 't Hooft-Polyakov monopole.)

The lift to M-theory of this situation is an M5-brane intersecting an M9-brane (see at M-theory on S1/G_HW times H/G_ADE):

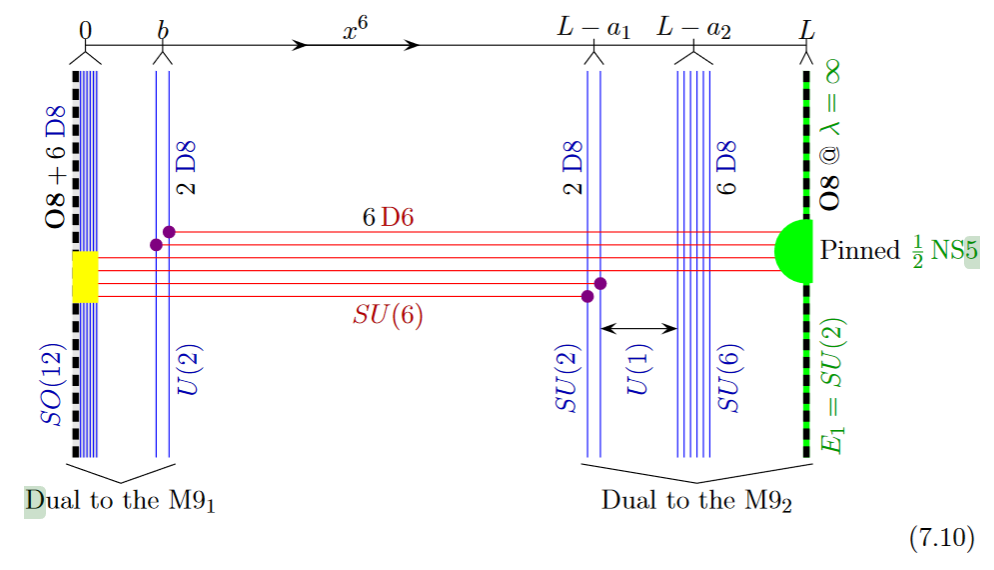
from GKSTY 02

Alternatively the O8-plane may intersect the black D6-branes away from the black NS5-brane:

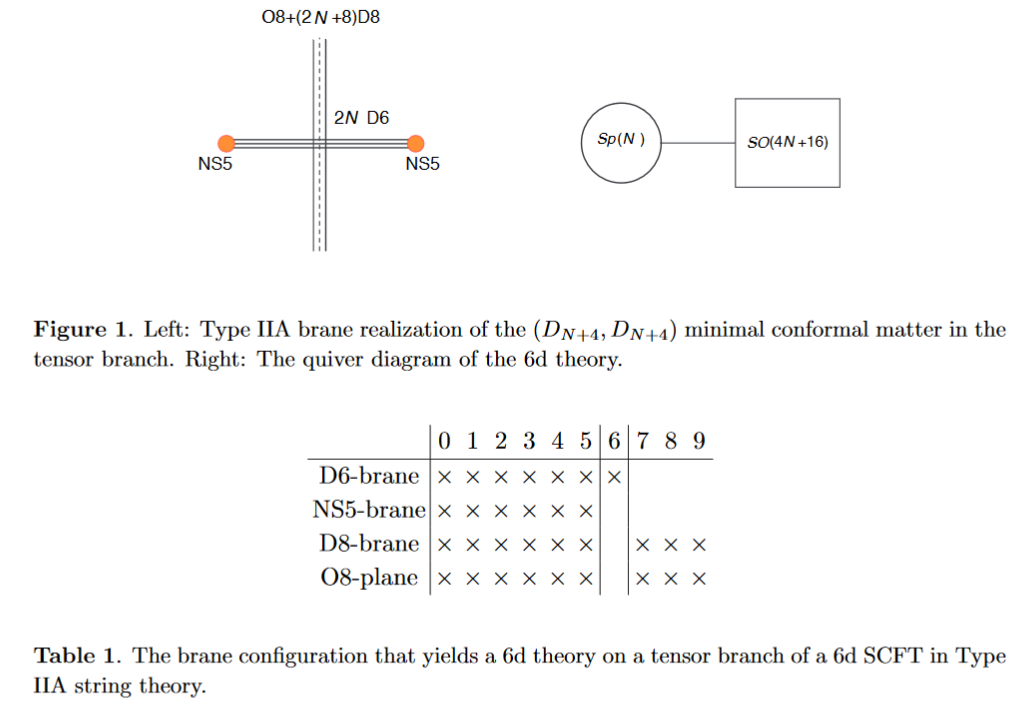
from HKLY 15

In general, some of the NS5 sit away from the O8-plane, while some sit on top of it:

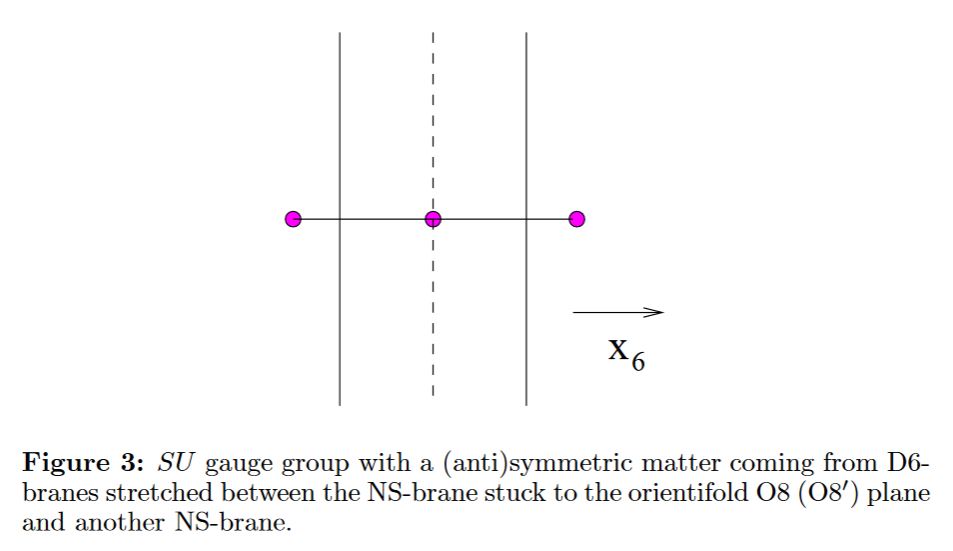
from Hanany-Zaffaroni 98

$I'$-theory on ADE-singularities intersecting O8-planes

(Bergman & Rodriguez-Gomez 12, Sec. 3)

(…)

Geometric engineering of $D = 6$ $N=(1,0)$ SCFTs on M5-branes

The M5-branes-configurations as above are supposed to geometrically engineer D=6 N=(1,0) SCFTs.

See the references below, for example DHTV 14, Section 6, Gaiotto-Tomasiello 14, HKLY 15.

Related concepts

KK-compactification of M-theory

• M-theory on a circle

• M-theory on 8-manifolds/on Spin(7)-manifolds

• M-theory on G₂-manifolds

  • G₂-MSSM

• M-theory on Sp(1)-manifolds

• M-theory on hyperbolic manifolds

• heterotic M-theory on ADE-orbifolds

• M-theory on Calabi-Yau manifolds

  • on CY2-folds

  • on CY3-folds

  • on CY4-folds

  • on CY5-folds

Dp-D(p+4)-brane bound states and Yang-Mills instantons

• D0-D4 brane bound state

• D1-D5 brane bound state

• D4-D8 brane bound state

• M5-MO9 brane bound state

References

General

The first discussion of this compactification is possibly

• Ashoke Sen, Section 3 of: A Note on Enhanced Gauge Symmetries in M- and String Theory, JHEP 9709:001,1997 (arXiv:hep-th/9707123)

in the context of the M-theory lift of gauge enhancement on D6-branes.

The original articles focusing on this situation:

• Michael Faux, Dieter Lüst, Burt Ovrut, Intersecting Orbifold Planes and Local Anomaly Cancellation in M-Theory, Nucl. Phys. B554: 437-483, 1999 (arXiv:hep-th/9903028)

• Michael Faux, Dieter Lüst, Burt Ovrut, Local Anomaly Cancellation, M-Theory Orbifolds and Phase-Transitions, Nucl. Phys. B589: 269-291, 2000 (arXiv:hep-th/0005251)

• Michael Faux, Dieter Lüst, Burt Ovrut, An M-Theory Perspective on Heterotic K3 Orbifold Compactifications, Int. J. Mod. Phys. A18:3273-3314, 2003 (arXiv:hep-th/0010087)

• Michael Faux, Dieter Lüst, Burt Ovrut, Twisted Sectors and Chern-Simons Terms in M-Theory Orbifolds, Int. J. Mod. Phys. A18: 2995-3014, 2003 (arXiv:hep-th/0011031)

• Vadim Kaplunovsky, Jacob Sonnenschein, Stefan Theisen, Shimon Yankielowicz, On the Duality between Perturbative Heterotic Orbifolds and M-Theory on $T^4/Z_N$, Nuclear Physics B Volume 590, Issues 1–2, 4 December 2000, Pages 123-160 Nuclear Physics B (arXiv:hep-th/9912144, doi:10.1016/S0550-3213(00)00460-0)

• E. Gorbatov, Vadim Kaplunovsky, Jacob Sonnenschein, Stefan Theisen, Shimon Yankielowicz, On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015 (2002) [arXiv:hep-th/0108135, doi:10.1088/1126-6708/2002/05/015]

Discussion of heterotic M-theory on smooth K3 originates around

• Nathan Seiberg, Edward Witten, Comments on String Dynamics in Six Dimensions, Nucl. Phys. B471:121-134, 1996 (arXiv:hep-th/9603003)

• Zygmunt Lalak, Steven Thomas, Gaugino Condensation, Moduli Potentials and Supersymmetry Breaking in M-Theory Models, Nuclear Physics B Volume 515, Issues 1–2, 30 March 1998, Pages 55-72 Nuclear Physics B (hep-th/9707223, doi:10.1016/S0550-3213(97)00784-0)

  (on gaugino condensation)

See also

• Jacob Cole Claussen, The deconstruction of orbifold fixed points in heterotic M-theory, 2016 (hdl:2152/41748)

• John Huerta, Hisham Sati, Urs Schreiber, Example 2.2.7 of: Real ADE-equivariant (co)homotopy and Super M-branes, CMP (2019) (arXiv:1805.05987, doi:10.1007/s00220-019-03442-3)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Section 4 of: Super-exceptional geometry: origin of heterotic M-theory and super-exceptional embedding construction of M5 (arXiv:1908.00042)

• Hisham Sati, Urs Schreiber, Section 4.1 of: Equivariant Cohomotopy implies orientifold tadpole cancellation (arXiv:1909.12277)

As $HET_E$-theory with ADE-singularities

As heterotic string theory on orbifold ADE-singularities:

• Edward Witten, Heterotic String Conformal Field Theory And A-D-E Singularities, JHEP 0002:025, 2000 (arXiv:hep-th/9909229)

As $I'$-theory with D6-branes

As type I' string theory with D6-branes:

• Ilka Brunner, Andreas Karch, Branes at Orbifolds versus Hanany Witten in Six Dimensions, JHEP 9803:003, 1998 (arXiv:hep-th/9712143)

• Amihay Hanany, Alberto Zaffaroni, Branes and Six Dimensional Supersymmetric Theories, Nucl.Phys. B529 (1998) 180-206 (arXiv:hep-th/9712145)

• Amihay Hanany, Alberto Zaffaroni, Monopoles in String Theory, JHEP 9912 (1999) 014 (arXiv:hep-th/9911113)

• Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Masato Taki, Futoshi Yagi, A new 5d description of 6d D-type minimal conformal matter, JHEP 1508:097, 2015 (arXiv:1505.04439)

• Ibrahima Bah, Achilleas Passias, Alessandro Tomasiello, $AdS_5$ compactifications with punctures in massive IIA supergravity, JHEP11 (2017)050 (arXiv:1704.07389)

and in massive type IIA string theory with D6-D8 brane bound states:

• Fabio Apruzzi, Marco Fazzi, AdS7/CFT6 with orientifolds, JHEP 01 (2018) 124 (arXiv:1712.03235)

As $I'$-theory with ADE-singularities

As type I' string theory at orbifold ADE-singularities:

• Oren Bergman, Diego Rodriguez-Gomez, Section 3 of: 5d quivers and their $AdS_6$ duals, JHEP07 (2012) 171 (arxiv:1206.3503)

• Chiung Hwang, Joonho Kim, Seok Kim, Jaemo Park, Section 3.4.2 of: General instanton counting and 5d SCFT, JHEP07 (2015) 063 (arxiv:1406.6793)

F-theory perspective

The F-theory perspective:

• Monika Marquart, Daniel Waldram, F-theory duals of M-theory on $S^1/\mathbb{Z}_2 \times T^4 / \mathbb{Z}_N$ (arXiv:hep-th/0204228)

• Christoph Lüdeling, Fabian Ruehle, F-theory duals of singular heterotic K3 models, Phys. Rev. D 91, 026010 (2015) (arXiv:1405.2928)

Geometric engineering of $D=6, \mathcal{N}=(1,0)$ SCFT

On D=6 N=(1,0) SCFTs via geometric engineering on M5-branes/NS5-branes at D-, E-type ADE-singularities, notably from M-theory on S1/G_HW times H/G_ADE, hence from orbifolds of type I' string theory (see at half NS5-brane):

• Michele Del Zotto, Jonathan Heckman, Alessandro Tomasiello, Cumrun Vafa, Section 6 of: 6d Conformal Matter, JHEP02(2015)054 (arXiv:1407.6359)

• Davide Gaiotto, Alessandro Tomasiello, Holography for $(1,0)$ theories in six dimensions, JHEP12(2014)003 (arXiv:1404.0711)

• Kantaro Ohmori, Hiroyuki Shimizu, $S^1/T^2$ Compactifications of 6d $\mathcal{N} = (1,0)$ Theories and Brane Webs, J. High Energ. Phys. (2016) 2016: 24 (arXiv:1509.03195)

• Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Futoshi Yagi, 6d SCFTs, 5d Dualities and Tao Web Diagrams, JHEP05 (2019)203 (arXiv:1509.03300)

• Ibrahima Bah, Achilleas Passias, Alessandro Tomasiello, $AdS_5$ compactifications with punctures in massive IIA supergravity, JHEP11 (2017)050 (arXiv:1704.07389)

• Santiago Cabrera, Amihay Hanany, Marcus Sperling, Magnetic Quivers, Higgs Branches, and 6d $\mathcal{N}=(1,0)$ Theories, J. High Energ. Phys. (2019) 2019: 71 (arXiv:1904.12293)

$SU(2)$-flavor symmetry on heterotic M5-branes

Emergence of SU(2) flavor-symmetry on single M5-branes in heterotic M-theory on ADE-orbifolds (in the D=6 N=(1,0) SCFT on small instantons in heterotic string theory):

• Abhijit Gadde, Babak Haghighat, Joonho Kim, Seok Kim, Guglielmo Lockhart, Cumrun Vafa, Section 4.2 of: 6d String Chains, J. High Energ. Phys. 2018, 143 (2018) (arXiv:1504.04614, doi:10.1007/JHEP02(2018)143)

• Kantaro Ohmori, Section 2.3.1 of: Six-Dimensional Superconformal Field Theories and Their Torus Compactifications, Springer Theses 2018 (springer:book/9789811330919)

Argument for this by translation under duality between M-theory and type IIA string theory to half NS5-brane/D6/D8-brane bound state systems in type I' string theory:

Reviewed in:

• Santiago Cabrera, Amihay Hanany, Marcus Sperling, Section 2.3 of: Magnetic Quivers, Higgs Branches, and 6d $\mathcal{N}=(1,0)$ Theories, JHEP06(2019)071, JHEP07(2019)137 (arXiv:1904.12293)

The emergence of flavor in these half NS5-brane/D6/D8-brane bound state systems, due to the semi-infinite extension of the D6-branes making them act as flavor branes:

• Amihay Hanany, Alberto Zaffaroni, Branes and Six Dimensional Supersymmetric Theories, Nucl.Phys. B529 (1998) 180-206 (arXiv:hep-th/9712145)

• Ilka Brunner, Andreas Karch, Branes at Orbifolds versus Hanany Witten in Six Dimensions, JHEP 9803:003, 1998 (arXiv:hep-th/9712143)

Reviewed in:

• Fabio Apruzzi, Marco Fazzi, Section 2.1 of: $AdS_7/CFT_6$ with orientifolds, J. High Energ. Phys. (2018) 2018: 124 (arXiv:1712.03235)

See also:

• Amihay Hanany, Noppadol Mekareeya, The Small $E_8$ Instanton and the Kraft Procesi Transition, JHEP07 (2018) 098 (arXiv:1801.01129)