nLab gaugino

Redirected from "gauginos".

Contents

Context

Fields and quanta

fields and particles in particle physics

and in the standard model of particle physics:

force field gauge bosons

photon - electromagnetic field (abelian Yang-Mills field)
W, Z, B-boson - electroweak field (Yang-Mills field)
gluon - strong nuclear force (Yang-Mills field)
graviton - field of gravity
infraparticle

scalar bosons

Higgs boson, inflaton (scalar field)

matter field fermions (spinors, Dirac fields)

flavors of fundamental fermions in the standard model of particle physics:
generation of fermions	1st generation	2nd generation	3d generation
quarks ( $q$ )
up-type	up quark ( $u$ )	charm quark ( $c$ )	top quark ( $t$ )
down-type	down quark ( $d$ )	strange quark ( $s$ )	bottom quark ( $b$ )
leptons
charged	electron	muon	tauon
neutral	electron neutrino	muon neutrino	tau neutrino

bound states:
mesons	light mesons: pion ( $u d$ ) ρ-meson ( $u d$ ) ω-meson ( $u d$ ) f1-meson a1-meson	strange-mesons: ϕ-meson ( $s \bar s$ ), kaon, K-meson ( $u s$ , $d s$ ) eta-meson ( $u u + d d + s s$ ) charmed heavy mesons*: D-meson ( $u c$ , $d c$ , $s c$ ) J/ψ-meson ( $c \bar c$ )	bottom heavy mesons: B-meson ( $q b$ ) ϒ-meson ( $b \bar b$ )
baryons	nucleons: proton $(u u d)$ neutron $(u d d)$

(also: antiparticles)

effective particles

Goldstone bosons

hadrons (bound states of the above quarks)

meson
- scalar meson
  - σ-meson
  - pion
  - kaon
  - D-meson
  - B-meson
- vector meson
  - ω-meson
  - ρ-meson
  - f1-meson
  - a1-meson
  - b1-meson
  - h1-meson
  - K*-meson
- tensor meson
- quarkonium
  - charmonium
  - ϒ-meson
exotic meson
- XYZ meson
- tetraquark
baryon
- nucleon
  - proton
  - neutron
  - chemical element
    - carbon
    - nitrogen
- Lambda baryon
- pentaquark

solitons

in grand unified theory

minimally extended supersymmetric standard model

superpartners

bosinos:

gravitino - field of supergravity (Rarita-Schwinger field)
gaugino - super Yang-Mills field
gluino

sfermions:

squark

dark matter candidates

WIMP
axion

Exotica

auxiliary fields

Idea

In quantum field theory the term gaugino denotes a field that is a superpartner of a gauge boson. This appears in super Yang-Mills theory. For instance the partner of a gluon in the MSSM is called a gluino, and so on.

In terms of Chern-Weil theory/differential cohomology we have that

gauge bosons are (the quanta of) connections on principal bundle or more generally the even components of superconnections;
gauginos are the odd components of superconnections.

Experiment

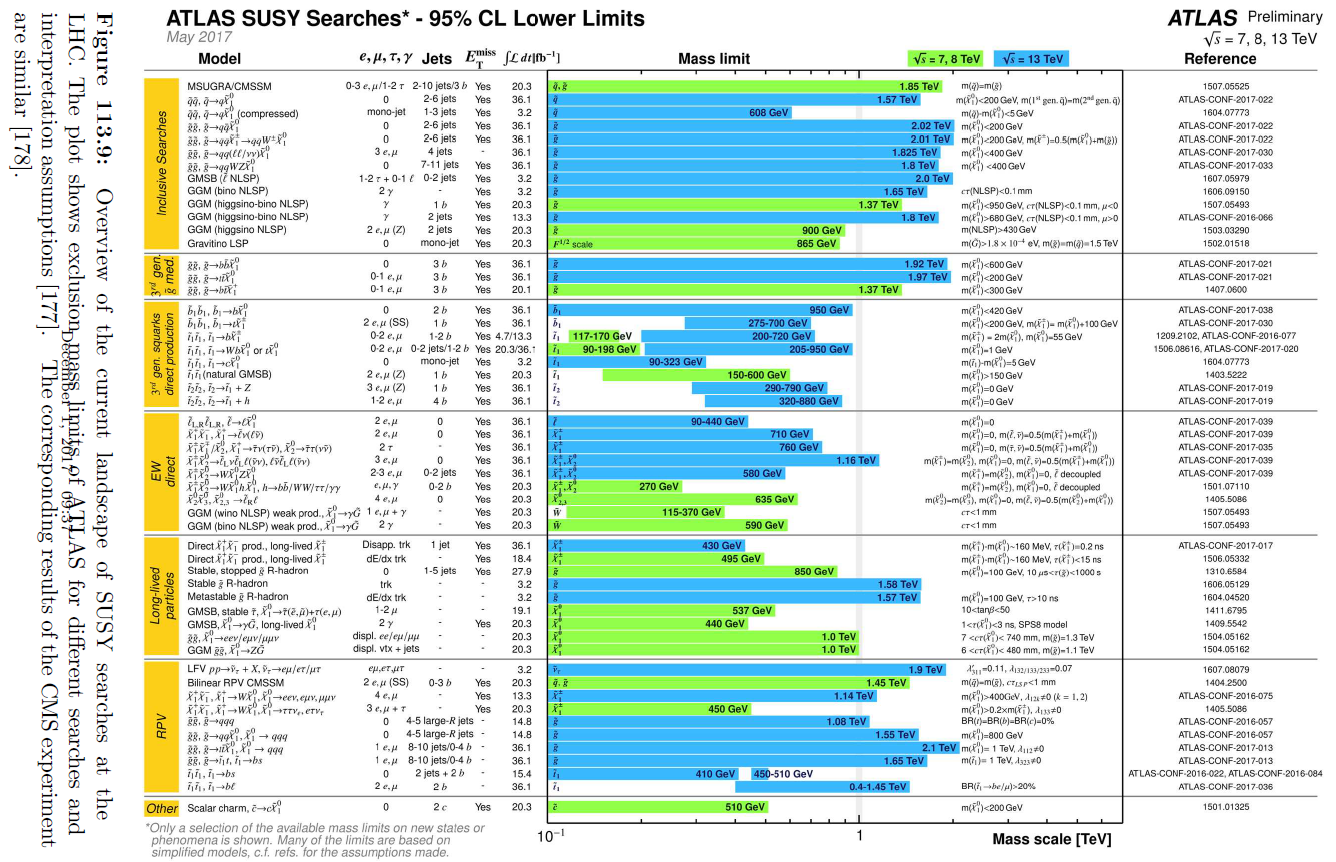
Experimental exclusion bounds of gluino rest masses due to the LHC experiment excludes gluinos/squarks of mass below about 3-4 TeV (Particle Data Group Review 17, figure 113.2 and 113.9):

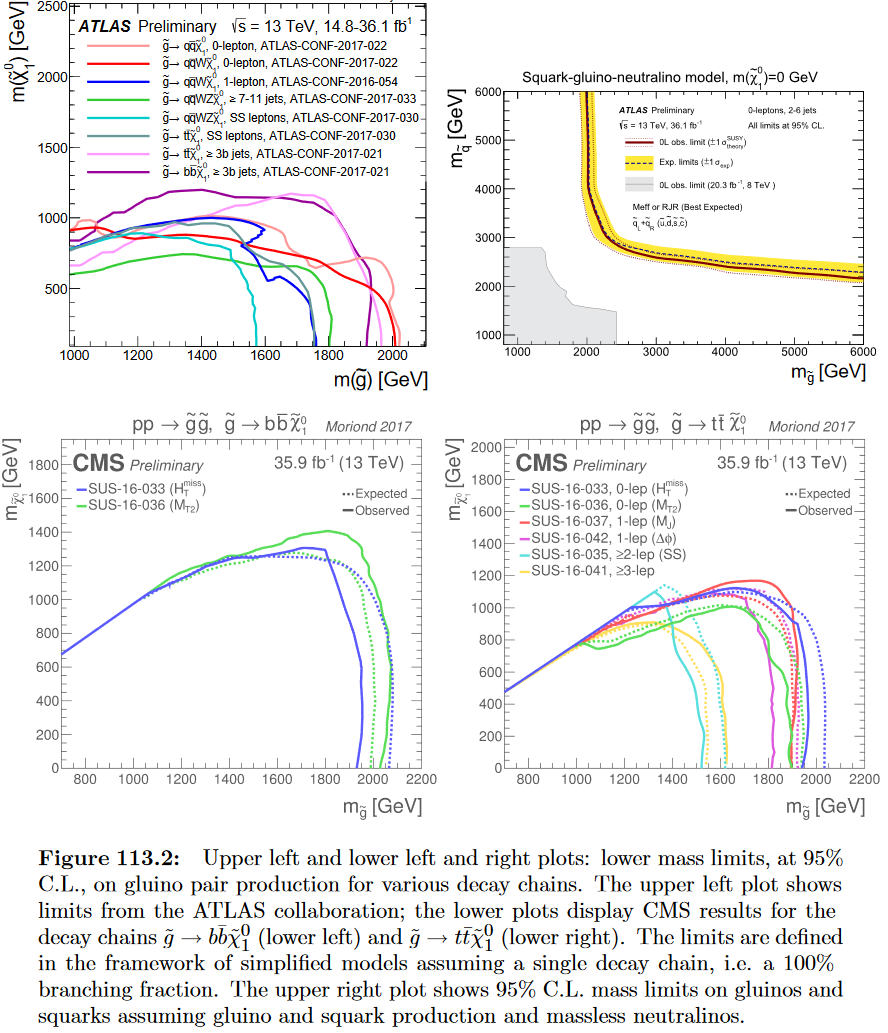
LHCSuperpartnerMassExclusion2017.png

Related concepts

in 10d super Yang-Mills theory: see there
sfermions
- squarks
split supersymmetry
gaugino condensation

References

Theoretical discussion includes

F. Gieres, Geometry of Supersymmetric Gauge Theories: Including an Introduction to BRS Differential Algebras and Anomalies Springer Lecture Notes in Physics 302 (1998)

Experimental exclusion bounds are discussed iin

Particle Data Group Review 2017, 113. Supersymmetry , part II (experiment) (pdf)

nLab gaugino

Context

Fields and quanta

Super-Geometry

Background

Introductions

Superalgebra

Supergeometry

Supersymmetry

Supersymmetric field theory

Applications

Contents

Idea

Experiment

Related concepts

References