nLab quantum parallelism

Idea

In quantum physics and specifically in quantum information theory, by quantum parallelism one means the property — to the extent that it holds, see below — of quantum processes and hence in particularly of quantum computations to potentially run “in parallel”, analogous to classical parallel computing.

Traditional accounts

In the literature, the notion of quantum parallelism is traditionally introduced either informally or by way of some explicit example, typically followed by some equally vague warning about not taking the parallelism too literally (e.g. Haroche & Raimond (2006), p. 96).

But it is easy to be fully precise about this phenomenon:

Formalization in quantum modal logic

Quantum parallelism is about direct sums of spaces of quantum states, hence about additive disjunction in their linear logic (in direct analogy to how quantum entanglement is about their tensor products and hence the multiplicative conjunction in their linear logic):

A quantum process $F \;\colon\; \mathscr{H} \multimap \mathscr{H}'$ (a linear map between spaces of quantum states, such as a quantum logic gate or quantum circuit) exhibits quantum parallelism to the extent that it is the image under the direct sum-functor of some $B$-indexed set of linear maps $F_b \;\colon\;\mathscr{H}_b \multimap \mathscr{H}'_b$:

$$F \;=\; \underset{b \colon B}{\oplus} F_b \;\colon\; \underset{b \colon B}{\bigoplus} \mathscr{H}_b \xrightarrow{\;\;} \underset{b \colon B}{\bigoplus} \mathscr{H}'_b \,.$$

In matrix calculus terms this means that we have a block-diagonal matrix. In quantum field theory such direct summands are also referred to as superselection sectors.

The caveat which traditional references try to allude to is that few interesting processes in experiment are of this pure direct sum form, while many interesting processes are composites of one of this form for the case that $b \colon B \;\vdash\; \mathscr{H}'_b = \mathscr{H}'_0$ with the codiagonal map on $\mathscr{H}'_0$

$$\array{ \underset{b \colon B}{\bigoplus} \mathscr{H}'_0 & \xrightarrow{\; codiag \;} & \mathscr{H}'_0 \\ \underset{b \colon B}{\oplus} \vert \psi_b \rangle &\mapsto& \underset{b \colon B}{\sum} \vert \psi_b \rangle }$$

This latter operation turns the “parallel” quantum states into a single quantum superposition from which the previous parallel components may not in general be recovered anymore.

(The ingenuity of quantum algorithms which do exhibit quantum advantage (such as Grover's algorithm or Shor's algorithm) is typically all in cleverly arranging the input to the computation such that some partial direct sum-decomposition is being retained after this superposition step.)

Conversely, if one does have a pure direct sum process pre-composed by the diagonal map on $\mathscr{H}_0$

$$\array{ \mathscr{H}'_0 & \xrightarrow{\; diag \;} & \underset{b \colon B}{\bigoplus} \mathscr{H}_0 \\ \vert \psi \rangle &\mapsto& \underset{b \colon B}{\oplus} \vert \psi \rangle }$$

then this pre-composition may be regarded as preparing a quantum states for parallel quantum computation on it.

The various fundamental quantum physics phenomena at play here may be identified with four modal-units of quantum modal logic (as discussed at quantum circuits via dependent linear types):

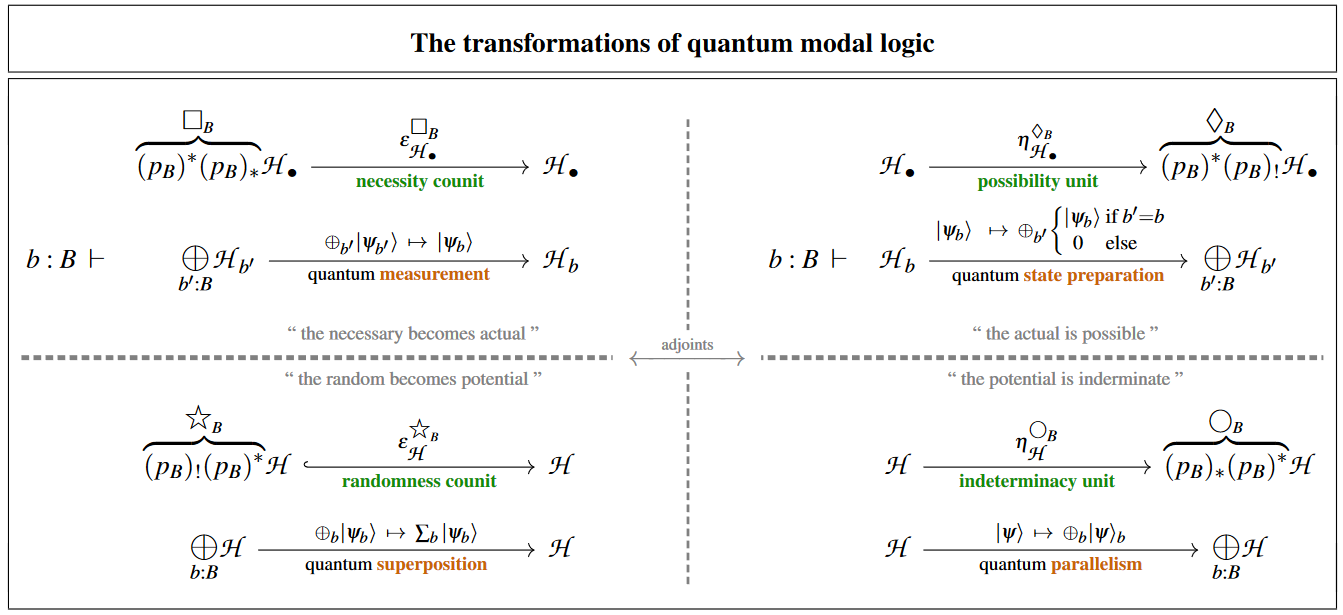
quantum measurement	quantum state preparation
quantum superposition	quantum parallelism

References

Traditional accounts:

• Serge Haroche, Jean-Michel Raimond, Exploring the Quantum: Atoms, Cavities, and Photons, Oxford University Press (2006) [doi:10.1093/acprof:oso/9780198509141.001.0001]