nLab Dalitz decay
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
In quantum hadrodynamics a Dalitz decay is the decay of an electrically neutral pseudoscalar meson into a dilepton pair and a either a photon (this is the original sense of Dalitz 51, a radiative leptonic decay) or a vector meson (a semileptonic decay).
Radiative leptonic Dalitz decay
In quantum hadrodynamics a Dalitz decay in the original sense (Dalitz 51) is the radiative leptonic decay of an electromagnetically neutral pseudoscalar meson into a photon and a dilepton:
The dominant contribution to this decay is by a purely radiative decay followed by an electron-photon interaction (“Dalitz pair”) of one of the two resulting photons (which thus participates as a virtual photon with spacelike wave vector ):
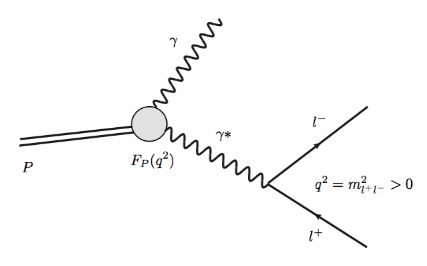
The original and archetypical example is the decay of the neutral pion into an electron/positron-pair and a photon:
The Feynman amplitude of the process is proportional to
where
-
is the Levi-Civita symbol,
-
is the wave vector and the polarization of the photon,
-
is the momentum of the (pseudo-)scalar meson,
-
is the lepton current
-
are the momenta of the two leptons, hence is that of the virtual photon mediating the decay.
(see Yia-Sang 09, (9) (symbol definition on p. 12), also e.g. KKN 02, p. 2, KKN06, p. 6 ).
Remark
The corresponding interaction Lagrangian density for the Feynman amplitude (1) (hence essentially its Fourier transform times the volume form) is, at fixed (all on 4d Minkowski spacetime):
where is the differential 1-form defined by the photon field (the gauge symmetry-connection-form), is the function (scalar field) which is the neutral component of the pion field and denotes is the de Rham differential.
Semileptonic Dalitz decay
More generally, one speaks of (generalized) Dalitz decays for the analogous process as above with the photon replaced by some vector meson, hence for semileptonic decays for and a pseudoscalar meson and vector meson, respectively, with dominant decay mode given by this Feynman diagram:

The Feynman amplitude of the process is, directly analogous to (1), proportional to
where
-
is the Levi-Civita symbol,
-
is the wave vector and the polarization of the vector meson,
-
is the momentum of the (pseudo-)scalar meson,
-
is the lepton current
-
are the momenta of the two leptons, hence is that of the virtual photon mediating the decay.
(e.g. Wachs 00, (2.60), FLQY 12, GLMY 19, (2))
Remark
The corresponding interaction Lagrangian density for the Feynman amplitude (3) (hence essentially its Fourier transform times the volume form) is, at fixed :
where is the differential 1-form defined by the vector meson field (the hidden local symmetry-connection-form), is the scalar field function which is the neutral component of the scalar meson field and denotes is the de Rham differential.
Remark
Up to possibly a global sign, it does not matter whether in (1) or (3) is taken to be the wave vector of the external photon/vector meson (as stated for instance in Yia-Sang 09, (9)) or of the interval virtual photon, equivalently of the dilepton pair (as stated for instance in FLQY 12, GLMY 19, (2)): Due to momentum conservation at the first interaction vertex their difference is proportional to the momentum of the scalar meson, and due to anti-symmetry of the Levi-Civita symbol this difference vanishes inside the above expression.
Equivalently, in terms of the Lagrangian density (4), this equivalence is reflected by Lagrangian densities defined only up to total derivative:
References
The original article:
- Richard Dalitz, On an alternative decay process for the neutral -meson, Proceedings of the Physical Society. Section A 64 (7), 667, 1951 (doi:10.1088/0370-1298/64/7/115)
Survey:
- M. Kunkel, Dalitz Decays of Pseudo-Scalar Mesons, talk at Light Meson Decays Workshop August 5, 2012 (pdf)
Further discussion of the Dalitz decay of pions:
-
Karol Kampf, Marc Knecht, Jiri Novotny, Some aspects of Dalitz decay , presented at Int. Conf. Hadron Structure ‘02, September 2002, Slovakia (arXiv:hep-ph/0212243)
-
Karol Kampf, Marc Knecht, Jiri Novotny, The Dalitz decay revisited, Eur. Phys. J. C46:191-217, 2006 (arXiv:hep-ph/0510021)
-
Esther Weil, Gernot Eichmann, Christian S. Fischer, Richard Williams, section III.A of: Electromagnetic decays of the neutral pion, Phys. Rev. D 96, 014021 (2017) (arXiv:1704.06046)
Dalitz decay of/into omega-mesons:
- Mirko Wachs, Die Selbstenergie des Omega-Mesons, 2000 (epda:000050)
Of pions and eta-mesons:
- Sergi González-Solís, Single and double Dalitz decays of , and mesons, Nuclear and Particle Physics Proceedings Volumes 258–259, January–February 2015, Pages 94-97 (doi:10.1016/j.nuclphysbps.2015.01.021)
Of pions, eta-mesons and omega-mesons:
- Henning Berghäuser, Investigation of the Dalitz decays and the electromagnetic form factors of the and -meson, 2010 (spire:1358057)
Discussion of Dalitz decay of quarkonium:
- Yu Jia, Wen-Long Sang, Observation prospects of leptonic and Dalitz decays of pseudoscalar quarkonia, JHEP 0910:090, 2009 (arXiv:0906.4782)
Of charmonium:
-
Jinlin Fu, Hai-Bo Li, Xiaoshuai Qin, Mao-Zhi Yang, Study of the electromagnetic transitions and probe dark photon, Modern Physics Letters A Vol. 27, No. 38, 1250223 (2012) (arXiv:1111.4055 doi:10.1142/S0217732312502239)
-
Study of the Dalitz decay , Phys. Rev. D 99, 012006 (2019) (arXiv:1810.03091)
Of upsilon-mesons:
- Li-Min Gu, Hai-Bo Li, Xin-Xin Ma, Mao-Zhi Yang, Study of the electromagnetic Dalitz decays , Phys. Rev. D 100, 016018 (2019) (arXiv:1904.06085)
Of baryons:
- G. Ramalho, A covariant model for the decuplet to octet Dalitz decays (arXiv:2002.07280)
Last revised on September 17, 2020 at 07:34:14. See the history of this page for a list of all contributions to it.