nLab G-CW complex
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Idea
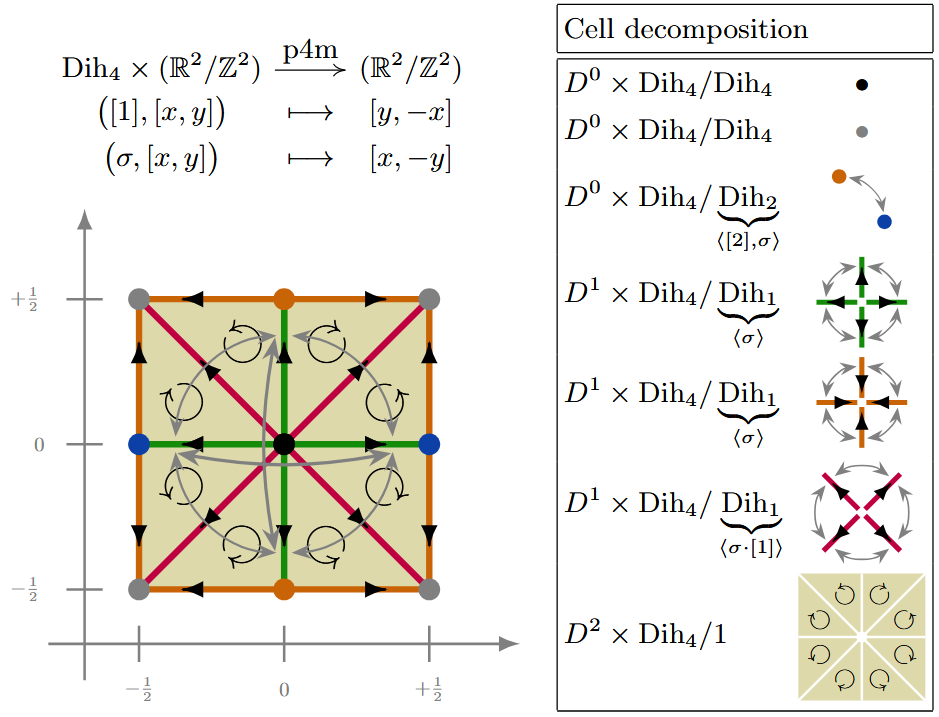
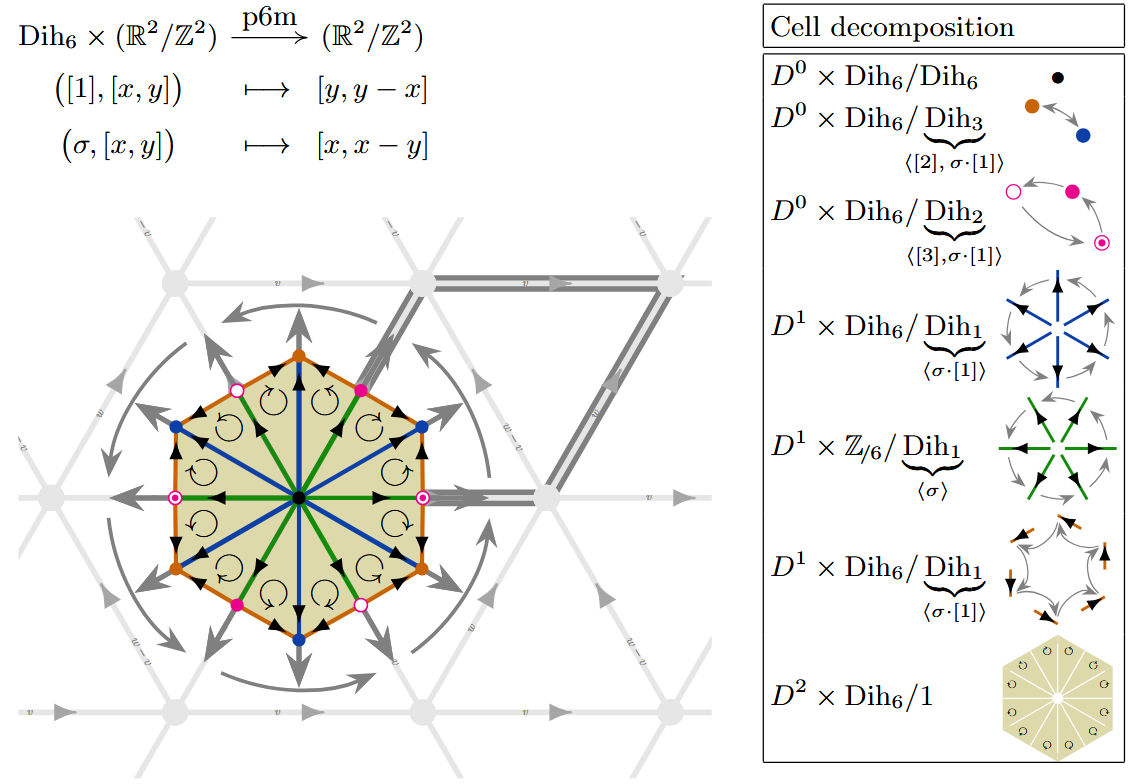
The concept of -CW complex is to that of CW-complexes as topological G-spaces are to topological spaces: for a compact topological group, the notion of -CW-complex is much like that of CW-complex, only that where in the latter case one builds a topological space from gluing of disks (“cells”) for a -CW-complex one glues products (product topological spaces) of disks with -orbits (coset spaces) for compact subgroups .
These are cofibrant objects in the -fine model structure on topological G-spaces.
Definition
Let the equivariance group be topological group (typically required to be a compact Lie group, see there).
As ranges over its closed subgroups, consider the coset spaces as G-spaces with respect to the residual left multiplication action by , and regard its product spaces and with the n-sphere and the n-disk, respectively, for the latter equipped with the trivial action.
This way, the canonical boundary inclusions
considered for ordinary CW-complexes induces -equivariant maps
Definition
A -CW-complex is a G-space isomorphic to the result of a sequence, monotone in cell dimension , of cell attachments via the -equivariant attaching maps (1).
Remark
For finite equivariance groups , a -CW-complex structure may be identified with
-
a plain CW-complex-structure
-
on which the -action is cellular (sends -cells onto -cells, respecting their boundaries)
-
which on cells that are sent to themselves actually restricts to the identity (i.e. cells that are fixed under the action are actually fixed point-wise).
This special case was the original definition on Bredon 1967b, I.1.
Examples
-Manifolds
The equivariant triangulation theorem says that if a compact Lie group acts on a compact smooth manifold , then the manifold admits an equivariant triangulation. In particular:
Proposition
For a compact Lie group, every closed smooth G-manifold admits the structure of a G-CW complex.
Moreover, if the manifold does have a boundary, then its G-CW complex may be chosen such that the boundary is a G-subcomplex. (Illman 83, last sentence above theorem 7.1)
In particular:
Proposition
(G-representation spheres are G-CW-complexes)
For a compact Lie group (e.g. a finite group) and a finite-dimensional orthogonal -linear representation, the representation sphere admits the structure of a G-CW-complex.
Simple examples of G-manifolds (above) are surfaces with -action, such as -tori (see below).
Equivariant cell structure on 2-tori
The following shows for the 2D crystallographic groups (wallpaper groups)
the -CW complex structure on the resulting G-tori (graphics from SS25).
The point groups arising are the cyclic groups , , , , and the dihedral groups , , , , and (making 9 distinct abstract point groups , due to the isomorphism , but several come with distinct group actions on ).
| wallpaper group | point group | G-cell structure on |
|---|---|---|
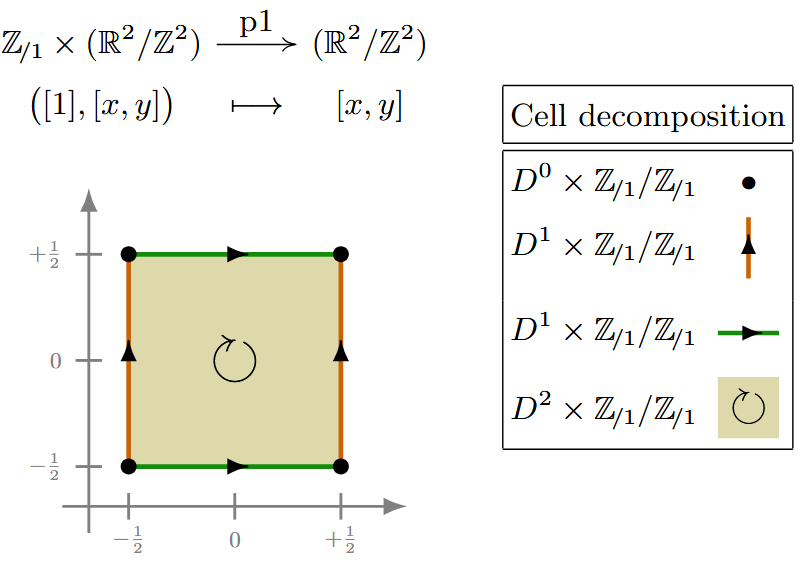
| p1 | Ex. | |
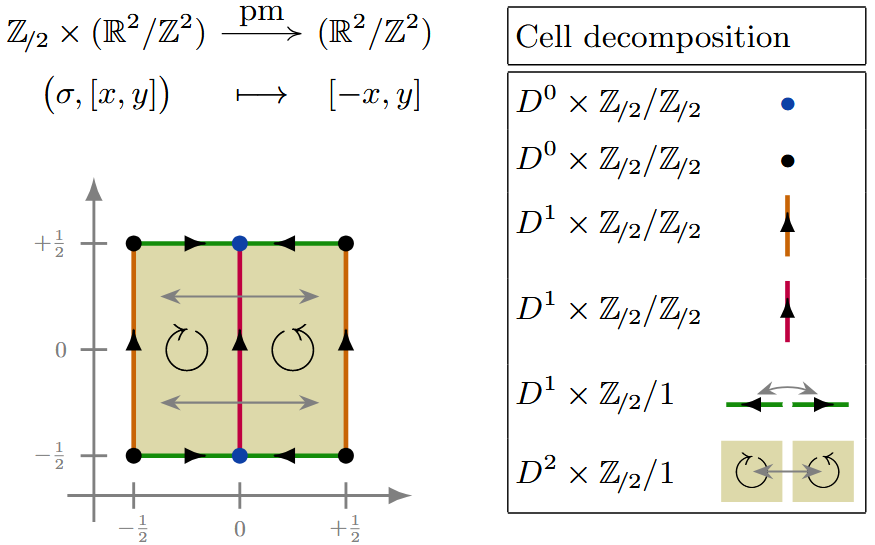
| pm | Ex. | |
| cm | Ex. | |
| pg | Ex. | |
| p2 | Ex. | |
| pmm | Ex. | |
| cmm | Ex. | |
| pmg | Ex. | |
| pgg | Ex. | |
| p3 | Ex. | |
| p31m | Ex. | |
| p3m1 | Ex. | |
| p4 | Ex. | |
| p4m | Ex. | |
| p4g | Ex. | |
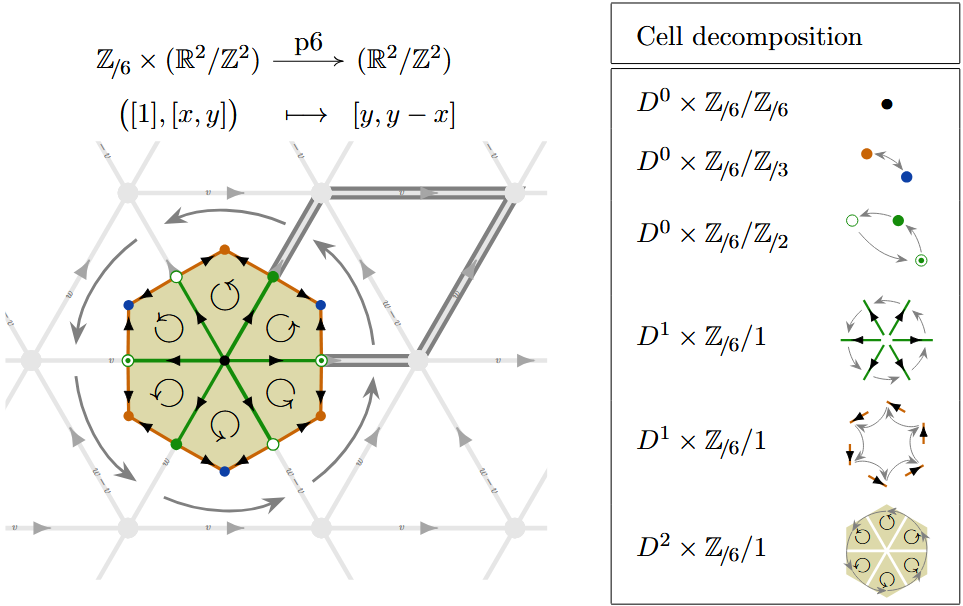
| p6 | Ex. | |
| p6m | Ex. |
Example
(p1) For completeness, here is a -CW complex structure for the torus equipped with trivial group-action, corresponding to the wallpaper group:
Example
(pm) Here is a -CW complex structure for the torus equipped with the -action which reflects one of the two coordinate axes, corresponding to the wallpaper group:
Example
(cm) Here is a -CW complex structure for the torus equipped with the -action which reflects along the coordinate diagonal, corresponding to the wallpaper group:
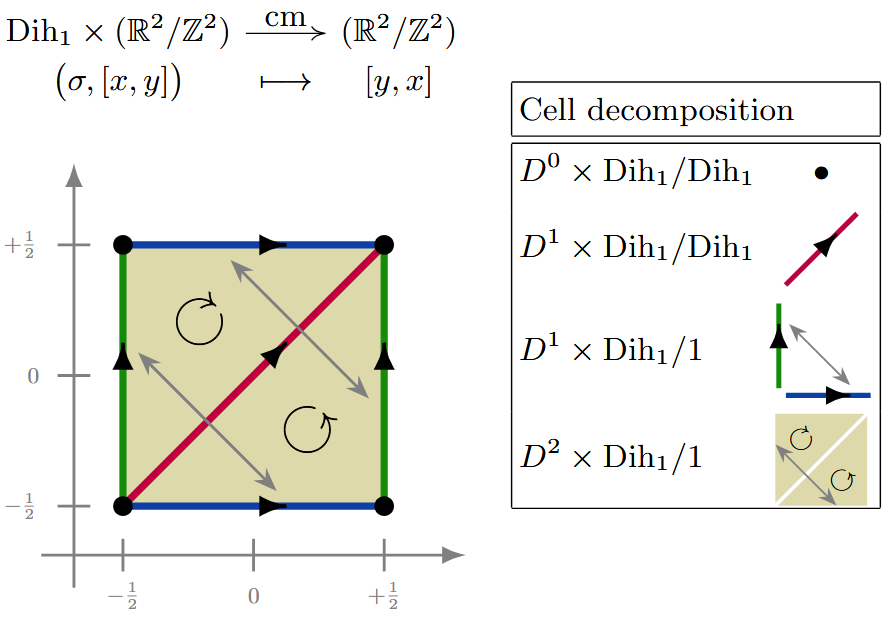
Example
(pg) Here is a -CW complex structure for the torus equipped with glide reflection action corresponding to the wallpaper group :
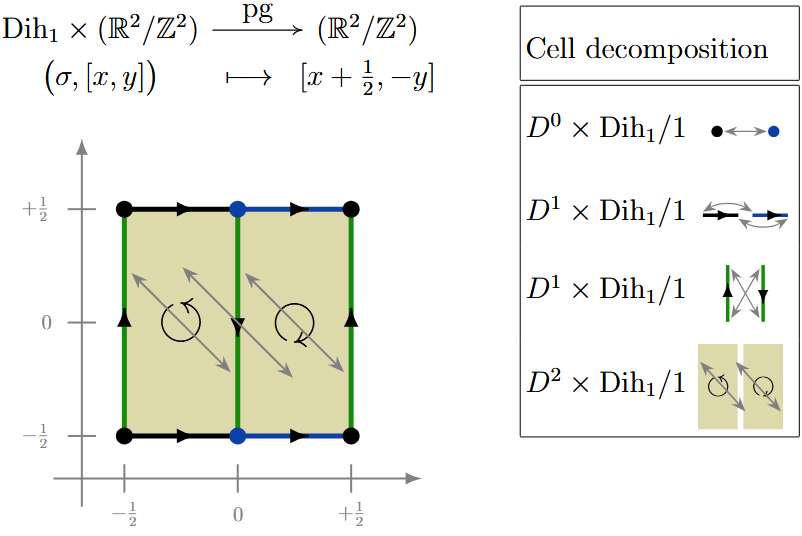
Example
(p2) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin, corresponding to the wallpaper group :
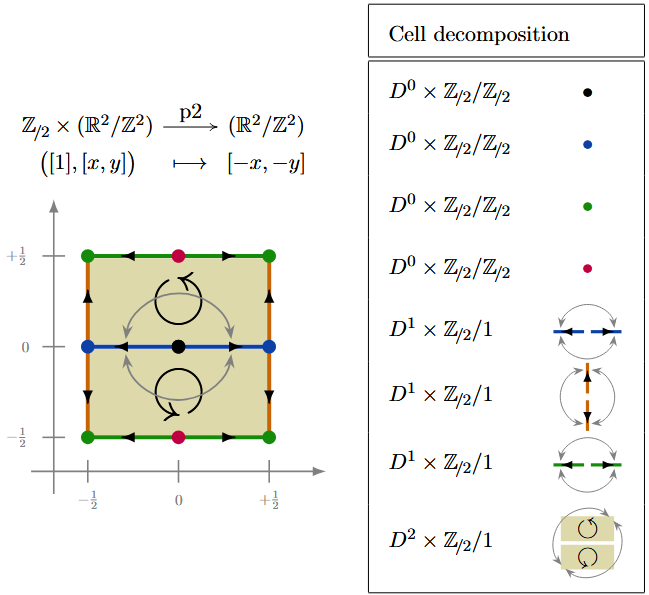
Example
(pmm) Here is a -CW complex structure for the torus equipped with -action according to the wallpaper group pmm:
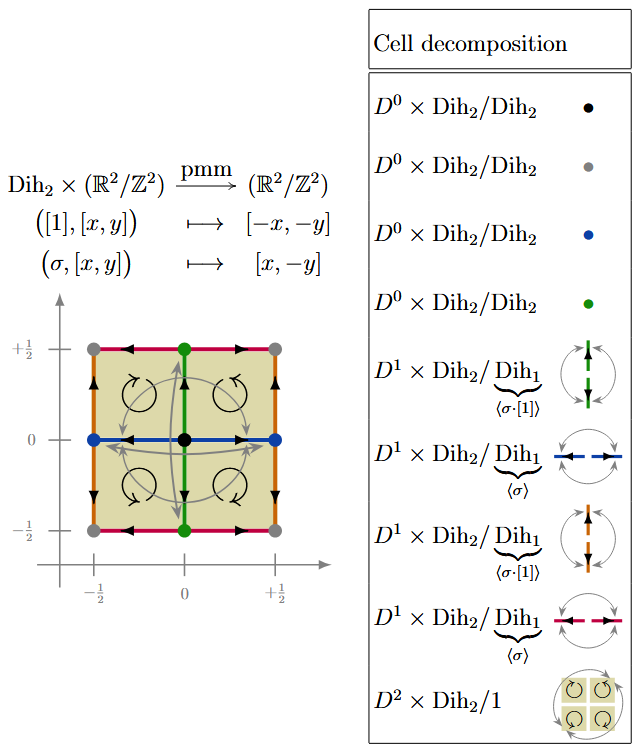
Example
(cmm) Here is a -CW complex structure for the torus equipped with -action according to the wallpaper group cmm:
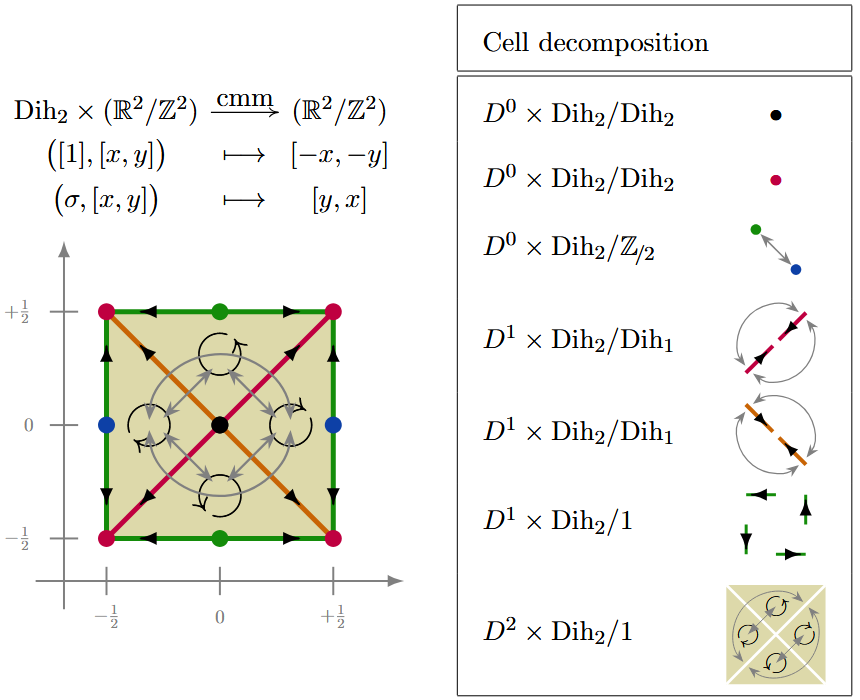
Example
(pmg) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
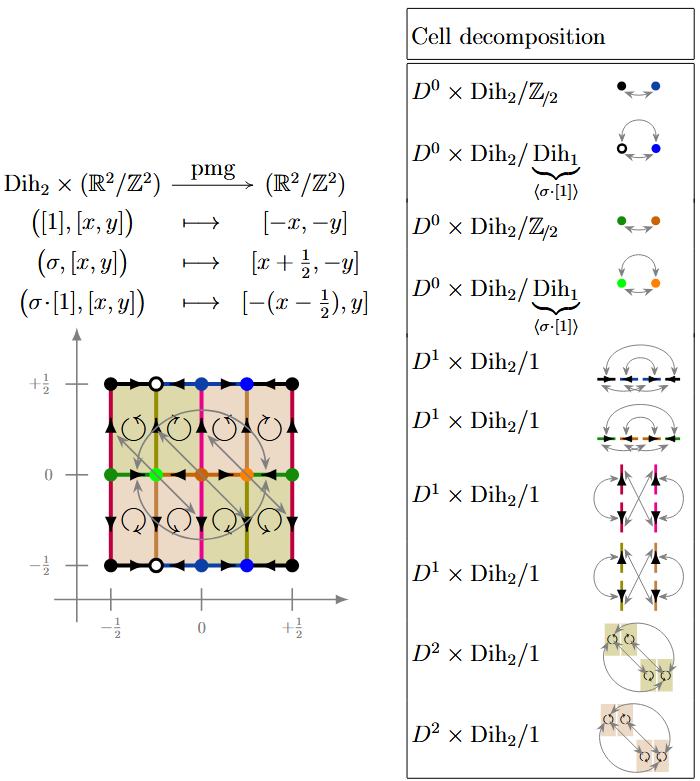
Example
(pgg) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
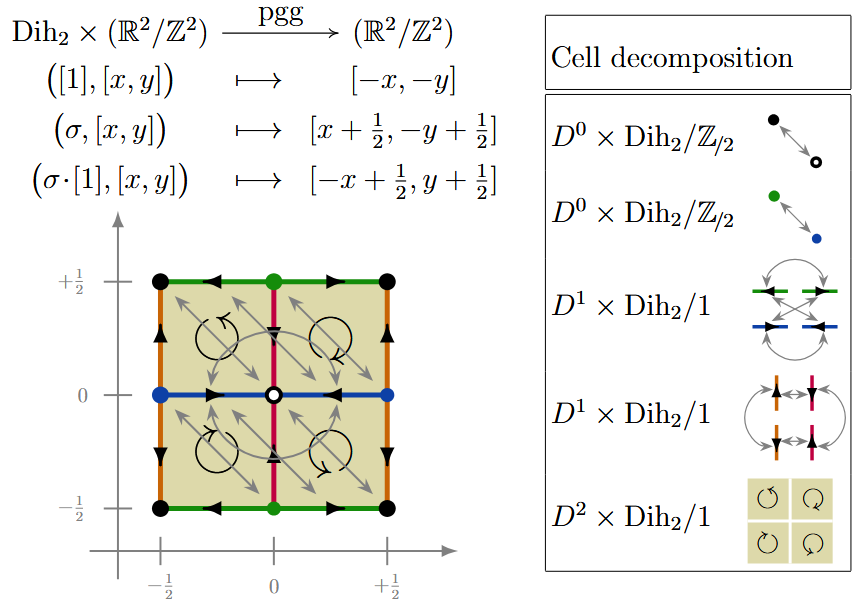
Example
(p3) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
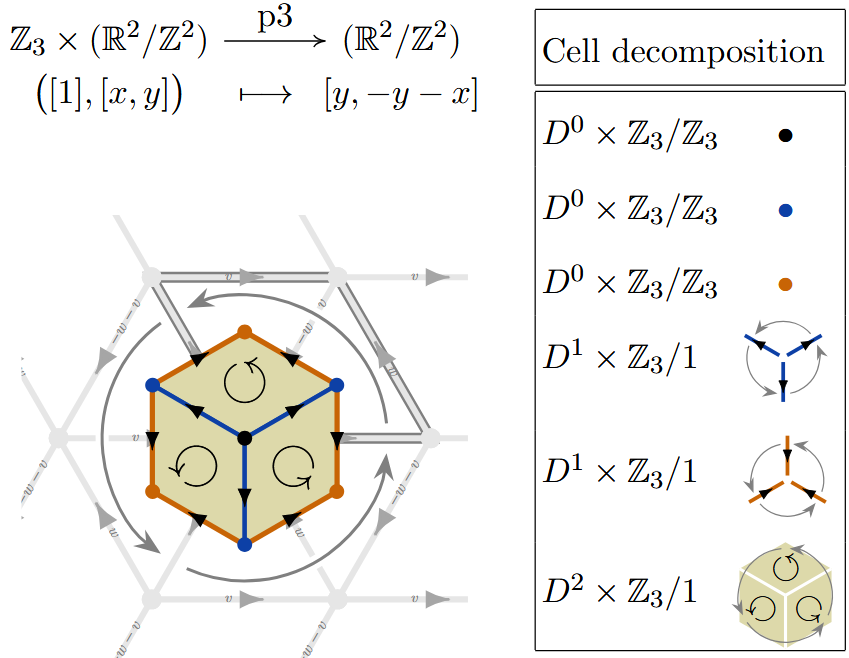
Example
(p31m) Here is a -CW complex structure for the torus equipped with -action corresponding to the wallpaper group:
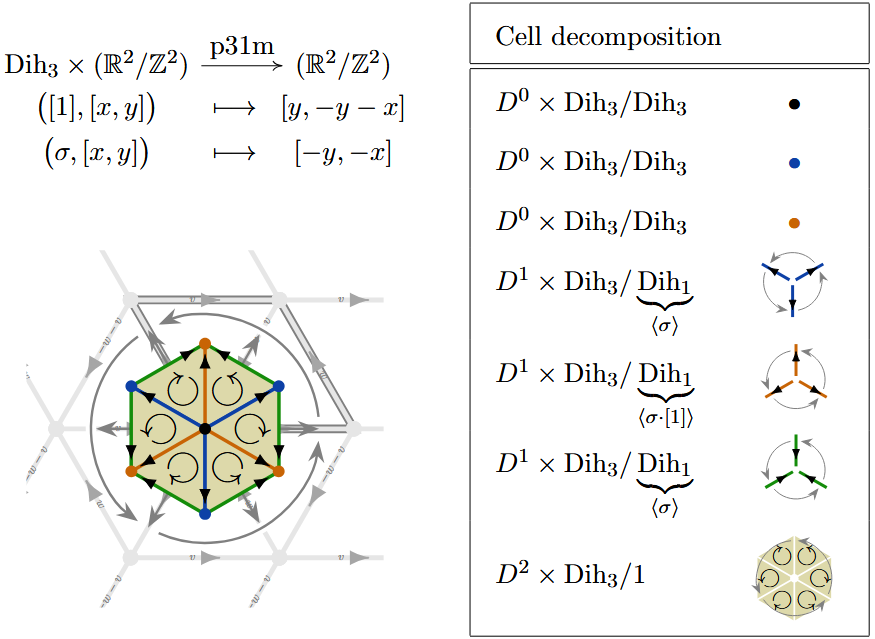
Example
(p3m1) Here is a -CW complex structure for the torus equipped with the -action corresponding to the wallpaper group:
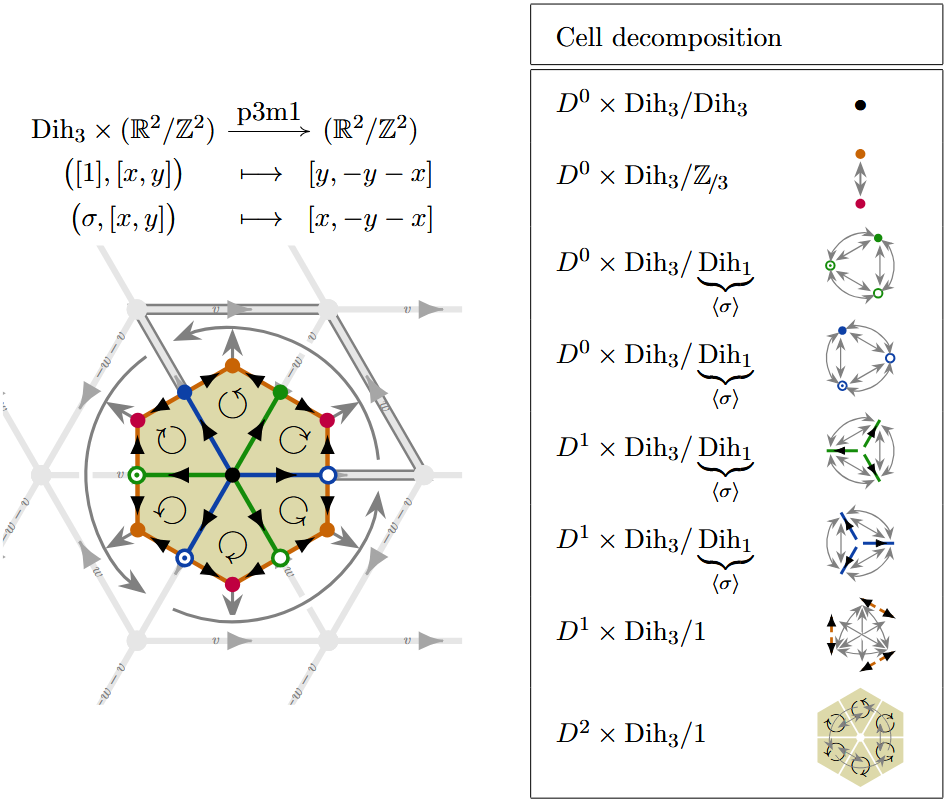
Example
(p4) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
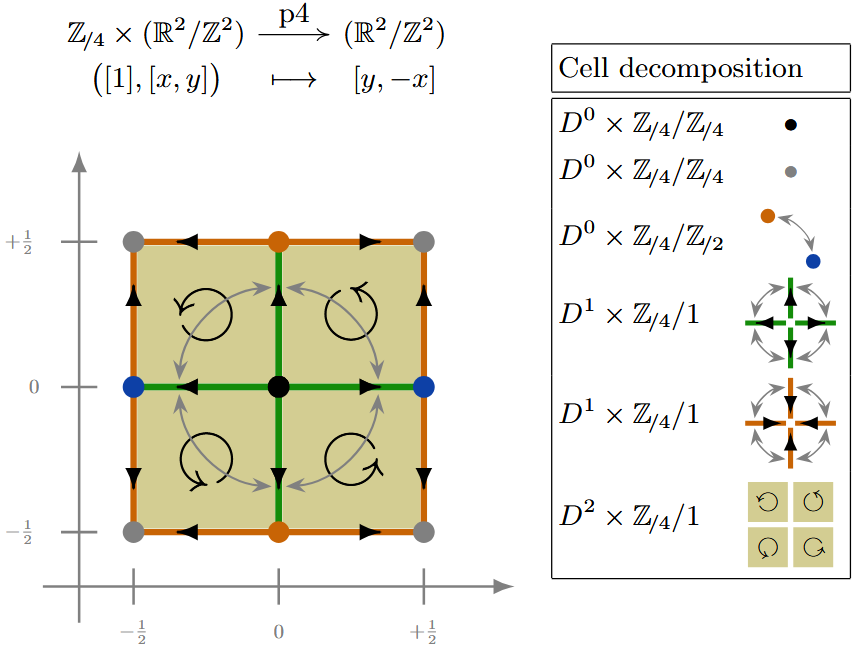
Example
(p4g) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
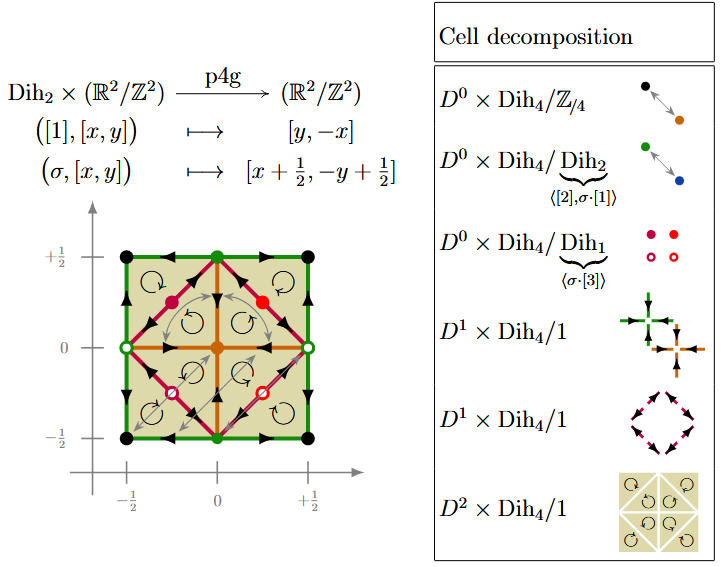
Example
(p6) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
Properties
Closure properties
Proposition
At least for a finite group, the product of two -CW-complexes in compactly generated weak Hausdorff spaces is itself a -CW-complex.
Proof
Since for finite , a -CW complex is the same as a plain CW-complex equipped with a cellular action by (Rem. ) it is clear that for this structure to be preserved by the product operation it is sufficient that the products of underlying cells constitute a CW-complex, hence that products preserve CW-complexes in compactly generated Hausdorff spaces. That is this the case is this Proposition.
Equivariant cellular approximation
See at equivariant cellular approximation theorem.
Equivariant CW-approximation
See at G-CW approximation.
Equivariant Whitehead theorem
See at equivariant Whitehead theorem.
Elmendorf’s theorem
See at Elmendorf's theorem.
References
The notion of G-CW complexes is, for the case of finite groups , due to
- Glen Bredon, Section I.1. of Equivariant cohomology theories, Springer Lecture Notes in Mathematics Vol. 34. 1967 (doi:10.1007/BFb0082690)
announced in
- Glen Bredon, Equivariant cohomology theories, Bull. Amer. Math. Soc. Volume 73, Number 2 (1967), 266-268. (educlid:1183528794)
In the broader generality of general topological groups and specifically of compact Lie groups, the notion of G-CW-complexes and their equivariant Whitehead theorem is due to:
-
Takao Matumoto, On -CW complexes and a theorem of JHC Whitehead, J. Fac. Sci. Univ. Tokyo Sect. IA 18 (1971) 363-374 [irdb:00926/0001786419, PDF]
-
Takao Matumoto, Equivariant K-theory and Fredholm operators, J. Fac. Sci. Tokyo 18 (1971/72), 109-112 (pdf, pdf)
and, independently, due to:
-
Sören Illman, Chapter I of: Equivariant algebraic topology, Princeton University 1972 (pdf)
-
Sören Illman, Section 2 of: Equivariant singular homology and cohomology for actions of compact lie groups (doi:10.1007/BFb0070055) In: H. T. Ku, L. N. Mann, J. L. Sicks, J. C. Su (eds.), Proceedings of the Second Conference on Compact Transformation Groups Lecture Notes in Mathematics, vol 298. Springer 1972 (doi:10.1007/BFb0070029)
-
Sören Illman, Section 2 of: Equivariant algebraic topology, Annales de l’Institut Fourier, Tome 23 (1973) no. 2, pp. 87-91 (doi:10.5802/aif.458)
(Which, in hindsight and with Elmendorf's theorem, gives a deeper justification for the parametrization over the orbit category already proposed in Bredon 67a, Bredon 67b.)
- Stefan Waner, Equivariant Homotopy Theory and Milnor’s Theorem, Transactions of the American Mathematical Society Vol. 258, No. 2 (Apr., 1980), pp. 351-368 (JSTOR)
Proof that -ANRs have the equivariant homotopy type of G-CW-complexes (for a compact Lie group):
- Slawomir Kwasik, On the Equivariant Homotopy Type of -ANR’s, Proceedings of the American Mathematical Society Vol. 83, No. 1 (Sep., 1981), pp. 193-194 (2 pages) (jstor:2043921)
Textbook accounts:
-
Tammo tom Dieck, Sections I.1 and I.2 of: Transformation Groups, de Gruyter 1987 (doi:10.1515/9783110858372)
-
Wolfgang Lück, Sections I.1, I.2 of: Transformation Groups and Algebraic K-Theory, Lecture Notes in Mathematics 1408 (Springer 1989) (doi:10.1007/BFb0083681)
-
Peter May et al., Section I.3 of: Equivariant homotopy and cohomology theory, CBMS Regional Conference Series in Mathematics, vol. 91, Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1996 (ISBN: 978-0-8218-0319-6 pdf, pdf)
Lecture notes:
- Andrew Blumberg, Equivariant homotopy theory, 2017 (pdf, GitHub)
Last revised on August 2, 2025 at 17:47:42. See the history of this page for a list of all contributions to it.