nLab quantum anomalous Hall effect

Redirected from "E-k operad".

Context

Quantum systems

Topological physics

Idea
Details
Related entries
References

Integer QAHE
Fractional QAHE

Idea

The quantum anomalous Hall effect (QAHE) is a joint variant of the quantum Hall effect and the anomalous Hall effect: Where a quantum Hall effect is induced by a strong external magnetic field, in the “anomalous” version — realized in crystalline topological phases of matter called Chern insulators — the effect of the external magnetic field on the electrons is instead mimicked by the latter’s spin-orbit coupling in the presence of magnetization, jointly reflected in a non-vanishing Berry curvature over the Brillouin torus which now plays the role of the external field’s flux density.

In analogy to how the ordinary quantum Hall effect has a fractional version, there is even a fractional version of the QAHE: the fractional quantum anomalous Hall effect (FQAHE).

Details

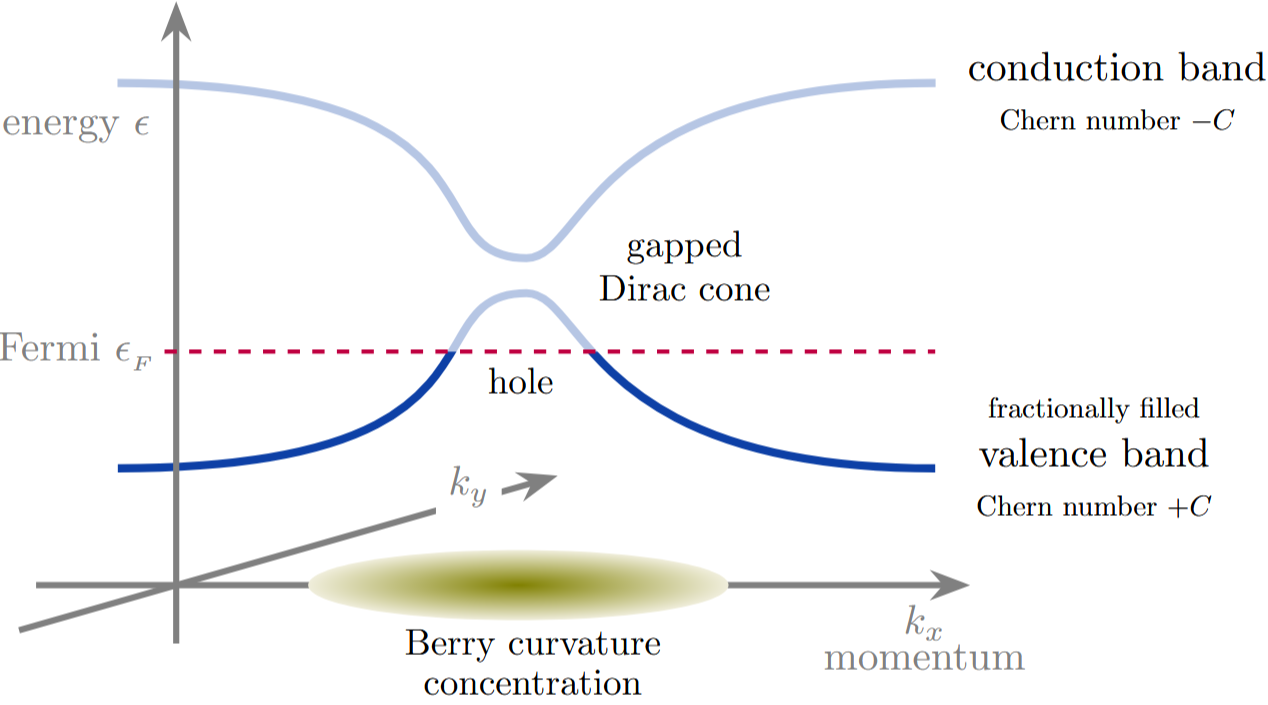
[Chang, Liu & MacDonald 2023 §II.A:] A common feature of all the QAH systems that are established as of this writing — magnetically doped TI films, films of the intrinsic magnetic TI $Mn Bi_2 Te_4$ , magic-angle TBG, ABC trilayer graphene on $h\text{-}BN$ , and TMD moirés — is adiabatic connection to a limit in which the band states close to the Fermi level can be described by 2D massive Dirac equations. […] The 2D Dirac model is not periodic in momentum and is therefore not a crystal Hamiltonian. When applied to crystalline electronic degrees of freedom, it is intended to apply only in small isolated portions of the Brillouin zone (BZ) with large Berry curvatures […] the Berry curvature in the 2D Dirac equation is concentrated within a momentum-space area proportional to $(m/\hbar v_D)^2$ (where $v_D \sim v_{D,x} \sim v_{D,y}$ ), and that it decays as ${\vert \mathbf{k} \vert}^{-3}$ for large ${\vert \mathbf{k} \vert}$ . […] Each 2D Dirac Hamiltonian therefore contributes $\pm (e^2/2 h)$ to the Hall conductivity

Moreover, for fractional quantum Hall systems the valence band:

is “almost flat”, meaning that its energy gradient with respect to momentum is small, so that the kinetic energy of electrons is small (“quenched”) and the electron-interaction/correlation is dominant
overlaps the Fermi energy, so that it is only partially (fractionally) filled, with holes at the peaks of the Dirac domes:

Related entries

Types of Hall effects

References

Integer QAHE

The theoretical prediction of Hall conductance proportional to the first Chern number (integrated Berry curvature) of the valence band in a topological insulator:

D. J. Thouless, M. Kohmoto, M. P. Nightingale, M. den Nijs: Quantized Hall Conductance in a Two-Dimensional Periodic Potential, Phys. Rev. Lett. 49 (1982) 405 [doi:10.1103/PhysRevLett.49.405]

The first theoretical lattice model, which came to be called the Haldane model:

Duncan Haldane: Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”, Phys. Rev. Lett. 61 (1988) 2015 [doi:10.1103/PhysRevLett.61.2015]

Experimental realization of QAH systems:

Cui-Zu Chang et al.: Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator, Science 340 (2013) 167 [doi:10.1126/science.1234414, arXiv:1605.08829]

Review:

Jing Wang, Biao Lian, Shou-Cheng Zhang: Quantum anomalous Hall effect in magnetic topological insulators, Physica Scripta 2015 T164 (2015) 014003 [arXiv:1409.6715, doi:10.1088/0031-8949/2015/T164/014003]
Chao-Xing Liu, Shou-Cheng Zhang, Xiao-Liang Qi: The Quantum Anomalous Hall Effect: Theory and Experiment, Annual Review of Condensed Matter Physics 7 (2016) [arXiv:1508.07106, doi:10.1146/annurev-conmatphys-031115-011417]
Cui-Zu Chang, Chao-Xing Liu, Allan H. MacDonald: Colloquium: Quantum anomalous Hall effect, Rev. Mod. Phys. 95 (2023) 011002 [arXiv:2202.13902, doi:10.1103/RevModPhys.95.011002]

Fractional QAHE

Theoretical prediction:

Titus Neupert, Luiz Santos, Claudio Chamon, Christopher Mudry: Fractional quantum Hall states at zero magnetic field, Phys. Rev. Lett. 106 (2011) 236804 [arXiv:1012.4723, doi:10.1103/PhysRevLett.106.236804]
S. A. Parameswaran, Rahul Roy, Shivaji L. Sondhi: Fractional Quantum Hall Physics in Topological Flat Bands, Comptes Rendus. Physique, Topological insulators / Isolants topologiques, 14 9-10 (2013) 816-839 [arXiv:1302.6606, doi:10.1016/j.crhy.2013.04.003]
Rahul Roy: Band geometry of fractional topological insulators, Phys. Rev. B 90 (2014) 165139 [arXiv:1208.2055, doi:10.1103/PhysRevB.90.165139]
Nicolas Regnault, B. Andrei Bernevig: Fractional Chern Insulator, Phys. Rev. X 1 (2011) 021014 [arXiv:1105.4867, doi:10.1103/PhysRevX.1.021014]

Experimental realization of FQAH systems:

Jiaqi Cai et al.: Signatures of Fractional Quantum Anomalous Hall States in Twisted $MoTe_2$ Bilayer, Nature 622 (2023) 63–68 [arXiv:2304.08470, doi:10.1038/s41586-023-06289-w]
Yihang Zeng et al.: Thermodynamic evidence of fractional Chern insulator in moiré $MoTe_2$ , Nature 622 (2023) 69–73 [doi:10.1038/s41586-023-06452-3]
Heonjoon Park et al.: Observation of fractionally quantized anomalous Hall effect, Nature 622 (2023) 74–79 [doi:10.1038/s41586-023-06536-0]
Zhengguang Lu et al.: Fractional quantum anomalous Hall effect in multilayer graphene, Nature 626 (2024) 759–764 [doi:10.1038/s41586-023-07010-7]