nLab anomalous Hall effect

Idea

The anomalous Hall effect is like a Hall effect but in the absence of a (substantial) external magnetic field, whose role is instead played by Berry curvature of the band, non-vanishing over the Brillouin torus of Bloch momenta, such as may be caused by intrinsic magnetization or strong spin-orbit coupling in the given crystalline material:

Like the ordinary Hall effect is caused by the Lorentz force which is exerted on electrons moving in “real” space filled with a magnetic flux density $F$ , so the anomalous Hall effect is caused analogously by an “anomalous velocity” contribution due to the Berry curvature $\Omega$ in momentum space.

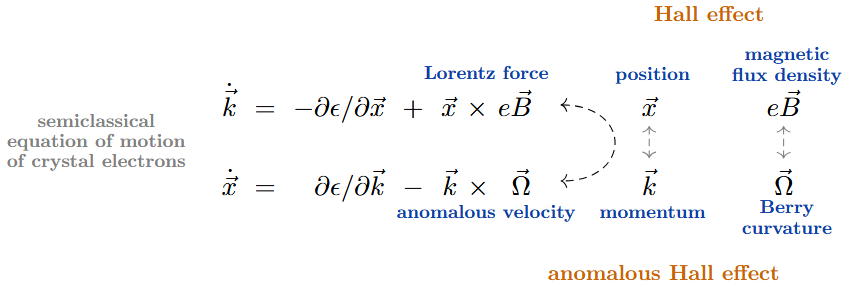
Historically, the microscopic understanding of the anomalous Hall effect had been slow and was riddled by debates. In modern understanding it is primarily due to non-vanishing Berry curvature over the Brillouin torus of the crystalline material, which plays the role of magnetic flux density in “reciprocal” momentum-space (cf. Sinitsyn 2008, Nagaosa et al 2010).

As such, the anomalous Hall effect is a “quantum” effect on par with the quantum Hall effect, and indeed the two combine in quantum anomalous Hall systems.

Types of Hall effects

The original observation:

Edwin H. Hall: On the “Rotational Coefficient” in Nickel and Cobalt, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science Series 5 Volume 12 Issue 74 (1881) [doi:10.1080/14786448108627086]

Review with emphasis on the explanation of anomalous velocity via Berry curvature:

Di Xiao, Junren Shi, Qian Niu: Berry phase correction to electron density of states in solids, Phys. Rev. Lett. 95 (2005) 137204 [arXiv:cond-mat/0502340, doi:10.1103/PhysRevLett.95.137204]
Nikolai A. Sinitsyn: Semiclassical theories of the anomalous Hall effect, Journal of Physics: Condensed Matter 20 2 (2008) [arXiv:0712.0183, doi:10.1088/0953-8984/20/02/023201]
Naoto Nagaosa, Jairo Sinova, Shigeki Onoda, Allan H. MacDonald, N. P. Ong: Anomalous Hall effect, Rev. Mod. Phys. 82 (2010) 1539 [arXiv:0904.4154, doi:10.1103/RevModPhys.82.1539]
Di Xiao, Ming-Che Chang, Qian Niu, section III.D of: Berry phase effects on electronic properties, Rev. Mod. Phys. 82 (2010) 1959 [arXiv:0907.2021, doi:10.1103/RevModPhys.82.1959]
David Vanderbilt, Section 5.1. of: Berry Phases in Electronic Structure Theory – Electric Polarization, Orbital Magnetization and Topological Insulators, Cambridge University Press (2018) [doi:10.1017/9781316662205]