nLab ADE singularity
Context
Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Contents
- Idea
- Properties
- Resolution by spheres touching along a Dynkin diagram
- From coincident KK-monopoles
- Bridgeland stability conditions
- Related concepts
- References
- General
- Via Bridgeland stability
- In string theory
- M-theory on ADE-orbifolds reducing to D6-branes in type II
- Heterotic M-theory on ADE-orbifolds
- Heterotic string theory on ADE-orbifolds
- Type II-string theory on ADE-orbifolds
- Type -string theory on ADE-orbifolds
- Type -string theory on ADE-orbifolds
- M-theory on -orbifolds with ADE-singularities
- F-theory with ADE-singularities
Idea
An ADE singularity is an orbifold fixed point locally of the form with a finite subgroup of SU(2) given by the ADE classification (and is understood with its defining linear action on the complex vector space ).
Properties
Resolution by spheres touching along a Dynkin diagram
The blow-up of an ADE-singularity is given by a union of Riemann spheres that touch each other such as to form the shape of the Dynkin diagram whose A-D-E label corresponds to that of the given finite subgroup of SU(2).
This statement is originally due to (duVal 1934 I, p. 1-3 (453-455)). A description in terms of hyper-Kähler geometry is due to Kronheimer 89a.
Quick survey of this fact is in Reid 87, a textbook account is Slodowy 80.
In string theory this fact is interpreted in terms of gauge enhancement of the M-theory-lift of coincident black D6-branes to an MK6 at an ADE-singularity (Sen 97):
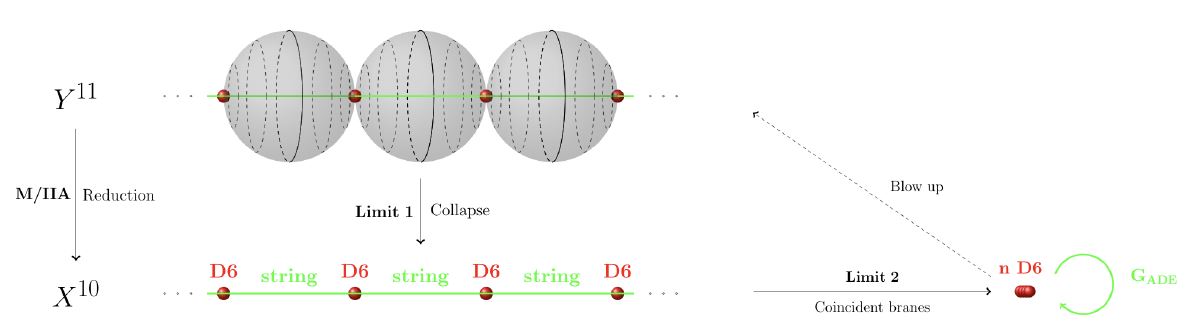
graphics grabbed from HSS18
See at M-theory lift of gauge enhancement on D6-branes for more.
ADE classification and McKay correspondence
From coincident KK-monopoles
| geometry transverse to KK-monopoles | Riemannian metric | remarks |
|---|---|---|
| Taub-NUT space: geometry transverse to distinct KK-monopoles at | (e.g. Sen 97b, Sect. 2) | |
| ALE space Taub-NUT close to close-by KK-monopoles e.g. close to : | e.g. via Euler angles: (e.g. Asano 00, Sect. 2) | |
| -type ADE singularity: ALE space in the limit where all KK-monopoles coincide at | (e.g. Asano 00, Sect. 3) |
Bridgeland stability conditions
For a finite subgroup of SU(2), let be the resolution of the corresponding ADE-singularity as above.
Then the connected component of the space of Bridgeland stability conditions on the bounded derived category of coherent sheaves over can be described explicitly (Bridgeland 05).
Specifically for type-A singularities the space of stability conditions is in fact connected and simply-connected topological space (Ishii-Ueda-Uehara 10).
Brief review is in Bridgeland 09, section 6.3.
Related concepts
References
General
Original articles include
-
Patrick du Val, On isolated singularities of surfaces which do not affect the conditions of adjunction. I, Proceedings of the Cambridge Philosophical Society, 30 (4): 453–459 (1934a) (doi:10.1017/S030500410001269X)
-
Patrick du Val, On isolated singularities of surfaces which do not affect the conditions of adjunction. II, Proceedings of the Cambridge Philosophical Society, 30 (4): 460–465 (1934) (doi:10.1017/S0305004100012706)
-
Patrick du Val, On isolated singularities of surfaces which do not affect the conditions of adjunction. III, Proceedings of the Cambridge Philosophical Society, 30 (4): 483–491 (1934) (doi:10.1017/S030500410001272X)
Textbook accounts include
-
Alan H. Durfee: Fifteen characterizations of rational double points and simple critical points, L’Enseignement Mathématique 25 (1979) [doi:10.5169/seals-50375, pdf]
-
Peter Slodowy: Simple singularities and simple algebraic groups, Lecture Notes in Mathematics 815, Springer (1980) [doi:10.1007/BFb0090294]
-
Klaus Lamotke, chapter IV of: Regular Solids and Isolated Singularities, Advanced Lectures in Mathematics, Vieweg (1986) [doi:10.1007/978-3-322-91767-6]
-
Miles Reid: Young persons guide to canonical singularities, in Spencer Bloch (ed.), Algebraic geometry – Bowdoin 1985, Part 1, Proc. Sympos. Pure Math. 46 Part 1, Amer. Math. Soc. (1987) 345-414 [pdf]
(The last formula on page 409 has a typo: there should be no in the denominator.)
Discussion of resolution of ADE-singularities in terms of hyper-Kähler geometry:
-
Peter Kronheimer, The construction of ALE spaces as hyper-Kähler quotients, J. Differential Geom. Volume 29, Number 3 (1989), 665-683. (euclid:1214443066)
-
Peter Kronheimer, A Torelli-type theorem for gravitational instantons, J. Differential Geom. Volume 29, Number 3 (1989), 685-697 (euclid:1214443067)
and in terms of preprojective algebras:
- William Crawley-Boevey, Martin P. Holland, Noncommutative deformations of Kleinian singularities, Duke Math. J. Volume 92, Number 3 (1998), 605-635 (euclid:1077231679)
Reviews and lecture notes:
-
Igor Burban, Du Val Singularities (pdf)
-
Miles Reid, The Du Val Singularities , , , , (pdf)
-
Anda Degeratu, Crepant Resolutions of Calabi-Yau Orbifolds, 2004 (pdf)
-
Kyler Siegel, section 6 of The Ubiquity of the ADE classification in Nature , 2014 (pdf)
-
MathOverflow, Resolving ADE singularities by blowing up
On the Chen-Ruan orbifold cohomology of ADE-singularities:
-
Fabio Perroni, Orbifold Cohomology of ADE-singularities (arXiv:0510528)
-
Fabio Perroni, Chen-Ruan cohomology of ADE-singularities, International Journal of Mathematics, Vol. 18, No. 9 (2007) 1009-1059 (arXiv:math/0605207, doi:10.1142/S0129167X07004436)
Families of examples of G₂ orbifolds with ADE singularities are constructed in
-
Frank Reidegeld, -orbifolds from K3 surfaces with ADE-singularities (arXiv:1512.05114)
-
Frank Reidegeld, -orbifolds with ADE-singularities (pdf)
Riemannian geometry of manifolds with ADE singularities is discussed in
- Boris Botvinnik, Jonathan Rosenberg, Positive scalar curvature on manifolds with fibered singularities (arXiv:1808.06007)
See also
- Wikipedia, du Val singularity
Via Bridgeland stability
Discussion of Bridgeland stability conditions for (resolutions of) ADE singularities includes:
-
Tom Bridgeland, Stability conditions and Kleinian singularities, International Mathematics Research Notices 2009.21 (2009): 4142-4157 (arXiv:0508257)
-
Akira Ishii, Kazushi Ueda, Hokuto Uehara, Stability conditions on -singularities, Journal of Differential Geometry 84 (2010) 87-126 (arXiv:math/0609551)
and specifically over Dynkin quivers
-
Yu Qiu, Def. 2.1 Stability conditions and quantum dilogarithm identities for Dynkin quivers, Adv. Math., 269 (2015), pp 220-264 (arXiv:1111.1010)
-
Tom Bridgeland, Yu Qiu, Tom Sutherland, Stability conditions and the quiver (arXiv:1406.2566)
In string theory
Discussion of ADE-singularities in string theory on orbifolds:
M-theory on ADE-orbifolds reducing to D6-branes in type II
M-theory lift of gauge enhancement on D6-branes:
-
Ashoke Sen, A Note on Enhanced Gauge Symmetries in M- and String Theory, JHEP 9709:001,1997 (arXiv:hep-th/9707123)
-
Luis Ibáñez, Angel Uranga, Section 6.3.3 of: String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012
Heterotic M-theory on ADE-orbifolds
heterotic M-theory on ADE-orbifolds:
-
Ashoke Sen, A Note on Enhanced Gauge Symmetries in M- and String Theory, JHEP 9709:001,1997 (arXiv:hep-th/9707123)
-
Michael Faux, Dieter Lüst, Burt Ovrut, Intersecting Orbifold Planes and Local Anomaly Cancellation in M-Theory, Nucl. Phys. B554: 437-483, 1999 (arXiv:hep-th/9903028)
-
Michael Faux, Dieter Lüst, Burt Ovrut, Local Anomaly Cancellation, M-Theory Orbifolds and Phase-Transitions, Nucl. Phys. B589: 269-291, 2000 (arXiv:hep-th/0005251)
-
Michael Faux, Dieter Lüst, Burt Ovrut, An M-Theory Perspective on Heterotic K3 Orbifold Compactifications, Int. J. Mod. Phys. A18:3273-3314, 2003 (arXiv:hep-th/0010087)
-
Michael Faux, Dieter Lüst, Burt Ovrut, Twisted Sectors and Chern-Simons Terms in M-Theory Orbifolds, Int. J. Mod. Phys. A18: 2995-3014, 2003 (arXiv:hep-th/0011031)
-
Vadim Kaplunovsky, J. Sonnenschein, Stefan Theisen, S. Yankielowicz, On the Duality between Perturbative Heterotic Orbifolds and M-Theory on , Nuclear Physics B Volume 590, Issues 1–2, 4 December 2000, Pages 123-160 Nuclear Physics B (arXiv:hep-th/9912144, doi:10.1016/S0550-3213(00)00460-0)
-
E. Gorbatov, Vadim Kaplunovsky, J. Sonnenschein, Stefan Theisen, S. Yankielowicz, On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015, 2002 (arXiv:hep-th/0108135)
-
John Huerta, Hisham Sati, Urs Schreiber, Real ADE-equivariant (co)homotopy and Super M-branes, CMP (2019) (arXiv:1805.05987, doi:10.1007/s00220-019-03442-3)
Heterotic string theory on ADE-orbifolds
heterotic string theory on ADE-orbifolds:
-
Paul Aspinwall, David Morrison, Point-like Instantons on K3 Orbifolds, Nucl. Phys. B503 (1997) 533-564 (arXiv:hep-th/9705104)
-
Edward Witten, Heterotic String Conformal Field Theory And A-D-E Singularities, JHEP 0002:025, 2000 (arXiv:hep-th/9909229)
Type II-string theory on ADE-orbifolds
The observation that the worldsheet 2d CFT correspoding to a string probing (a D-brane on) an -type singularity is the chiral WZW model for the affine Lie algebra su(2) at level (plus some trivial summands):
-
Hirosi OoguriCumrun Vafa, p. 10-12 of: Two-Dimensional Black Hole and Singularities of CY Manifolds, Nucl. Phys. B 463 (1996) 55-72 (arXiv:hep-th/9511164, doi:10.1016/0550-3213%2896%2900008-9)
-
Wolfgang Lerche, Carsten Andrew Lütken, Christoph Schweigert, p. 4 of: D-Branes on ALE Spaces and the ADE Classification of Conformal Field Theories, Nucl.Phys. B 622 (2002) 269-278 (doi:10.1016/S0550-3213%2801%2900613-7, arXiv:hep-th/0006247)
On how this -CFT encodes the BPS states of -SYM on D3-branes transverse to the singularity:
- Wolfgang Lerche, On a Boundary CFT Description of Nonperturbative Yang-Mills Theory (arXiv:hep-th/0006100)
An interpretation of this phenomenon, under the expected K-theory classification of D-brane charge, as due to the (somewhat neglected) sector of twisted equivariant K-theory where the twist is by an inner local system which may appear inside an A-type singularity:
- Hisham Sati, Urs Schreiber, (around p. 23 of) Anyonic defect branes in TED-K-theory (arXiv:2203.11838)
Type -string theory on ADE-orbifolds
type I' string theory on ADE-orbifolds
- Oren Bergman, Diego Rodriguez-Gomez, Section 3 of: 5d quivers and their duals, JHEP07 (2012) 171 (arxiv:1206.3503)
Type -string theory on ADE-orbifolds
type I string theory on ADE-orbifolds
- Kenneth Intriligator, New String Theories in Six Dimensions via Branes at Orbifold Singularities, Adv. Theor. Math. Phys.1:271-282, 1998 (arXiv:hep-th/9708117)
M-theory on -orbifolds with ADE-singularities
M-theory on G₂-manifolds with ADE-singularities:
-
Bobby Acharya, M theory, Joyce Orbifolds and Super Yang-Mills, Adv. Theor. Math. Phys. 3 (1999) 227-248 (arXiv:hep-th/9812205)
-
Bobby Acharya, On Realising Super Yang-Mills in M theory (arXiv:hep-th/0011089)
-
Bobby Acharya, B. Spence, Flux, Supersymmetry and M theory on 7-manifolds (arXiv:hep-th/0007213)
-
Bobby Acharya, M Theory, -manifolds and Four Dimensional Physics, Classical and Quantum Gravity Volume 19 Number 22, 2002 (pdf)
-
Michael Atiyah, Juan Maldacena, Cumrun Vafa, An M-theory Flop as a Large N Duality, J. Math. Phys.42:3209-3220, 2001 (arXiv:hep-th/0011256)
-
Chris Beasley, Edward Witten, A Note on Fluxes and Superpotentials in M-theory Compactifications on Manifolds of Holonomy, JHEP 0207:046 (2002) (arXiv:hep-th/0203061)
-
Michael Atiyah, Edward Witten M-Theory dynamics on a manifold of -holonomy, Adv. Theor. Math. Phys. 6 (2001) (arXiv:hep-th/0107177)
-
Edward Witten, Anomaly Cancellation On Manifolds Of Holonomy (arXiv:hep-th/0108165)
-
Bobby Acharya, Edward Witten, Chiral Fermions from Manifolds of Holonomy (arXiv:hep-th/0109152)
-
Ron Donagi, Martin Wijnholt: The M-Theory Three-Form and Singular Geometries [arXiv:2310.05838]
F-theory with ADE-singularities
F-theory with ADE-singularities
- Paul Aspinwall, David Morrison, Point-like Instantons on K3 Orbifolds, Nucl. Phys. B503 (1997) 533-564 (arXiv:hep-th/9705104)
See also at F-branes – table
Last revised on June 23, 2025 at 11:07:42. See the history of this page for a list of all contributions to it.