nLab Taub-NUT space
Context
Riemannian geometry
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
Idea
A kind of spacetime. For the moment see at KK-monopole for more.
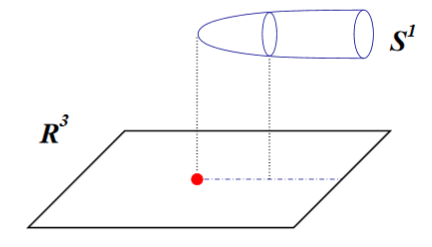
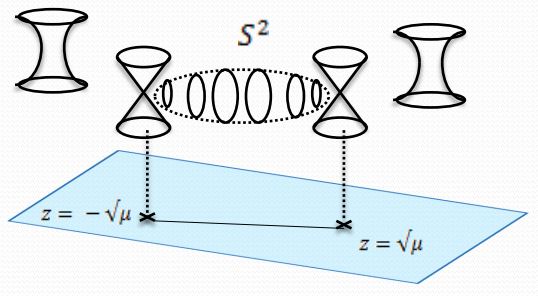
graphics grabbed from Acharya-Gukov 04
Consider the left invariant 1-forms on the 3-sphere SU(2), which in terms of Euler angles are
Then the pseudo-Riemannian metric defining the Taub-NUT geometry is
Properties
Relation to KK-monopoles
| geometry transverse to KK-monopoles | Riemannian metric | remarks |
|---|---|---|
| Taub-NUT space: geometry transverse to distinct KK-monopoles at | (e.g. Sen 97b, Sect. 2) | |
| ALE space Taub-NUT close to close-by KK-monopoles e.g. close to : | e.g. via Euler angles: (e.g. Asano 00, Sect. 2) | |
| -type ADE singularity: ALE space in the limit where all KK-monopoles coincide at | (e.g. Asano 00, Sect. 3) |
Relation to D6-branes
from M-branes to F-branes: superstrings, D-branes and NS5-branes
(e.g. Johnson 97, Blumenhagen 10)
Related concepts
References
-
Wikipedia, Taub-NUT space
-
Wikipedia, Gravitational instanton
-
Luis Ibáñez, Angel Uranga, section 6.3.3 of String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012
Discussion in the context of M-theory on G₂-manifolds and gauge enhancement
- Bobby Acharya, Sergei Gukov, section 5.2 of M theory and Singularities of Exceptional Holonomy Manifolds, Phys.Rept.392:121-189,2004 (arXiv:hep-th/0409191)
Last revised on July 18, 2024 at 11:24:56. See the history of this page for a list of all contributions to it.
 (
(