nLab pion
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
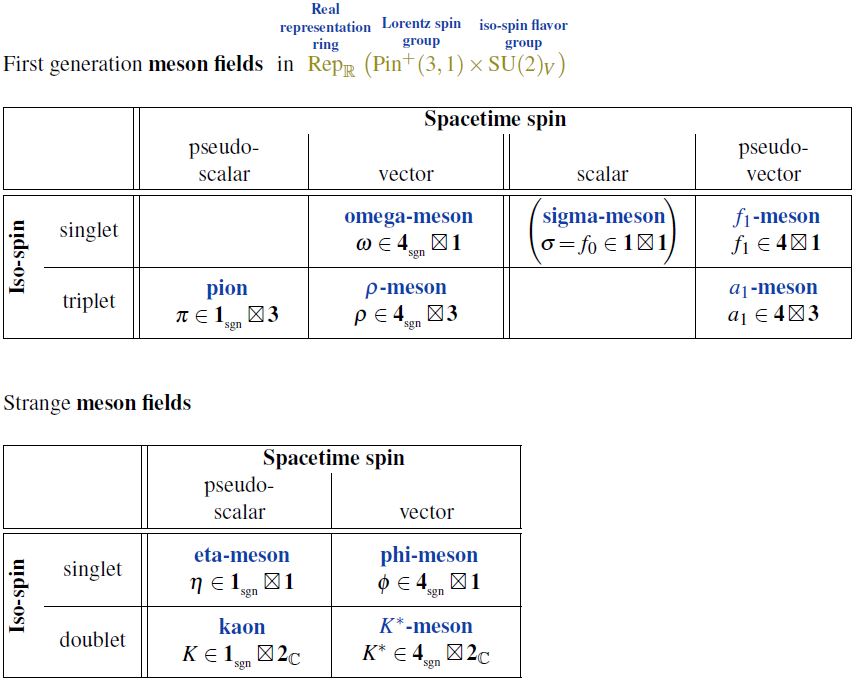
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
In nuclear physics, specifically in the chiral perturbation theory of quantum chromodynamics, the pion or pi-meson (-meson) is the isospin-triplet scalar-meson field in the first-generation of fermions, i.e. a bound state of an up quark and a down quark (a light meson):
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
Details
As the Goldstone boson of chiral symmetry breaking
From the point of view of the quark-model of nuclear physics, the pion is the Goldstone boson corresponding to the spontaneous symmetry breaking of the “chiral”-symmetry group to the diagonal subgroup , by the vacuum expectation value of the quark-condensate.
(e.g. Machleidt-Entem 11, 2.1.3)
Plain pion field
Hence, in the sense of the Wigner classification, the pion field transforms in the sign representation of the Lorentz group/Pin group (is a spacetime pseudoscalar) and in the adjoint representation of the isospin group SU(2)
As such, a pion field history is a smooth function from spacetime to the Lie algebra su(2)
where the vecotr notation on the left is to indicate that this is, at each spacetime point (event) , an element in a real 3-dimensional vector space
This means that for any choice of linear basis of , the pion field decomposes as three real-valued fields.
In the nuclear physics-literature the common choice is that corresponding to the Cartan-Weyl basis
in terms of which the components of the pion field are hence denoted as follows
| pion field component | quark bound state |
|---|---|
| or | |
Exponentiated pion field
Especially in chiral perturbation theory, the pion field is typically represented as the exponentiation of (1) to an SU(2)-valued field
(Witten 83, (2), Adkins-Nappi 84, (1)-(3)) nowadays called the exponentiated pion field or often just the chiral field, for review see Machleidt-Entem 11, (2.29), Rho et al. 16, around (1).
Here the unit is called the pion decay constant.
Assuming that the pion field vanishes at spatial infinity hence means that the exponentiated pion field is a map
from (the time-axis times) the 3-sphere to SU(2). The homotopy class of this continuous function, an element of the (co-)homotopy group of spheres , is the Skyrmion-number, or, in fact, the baryon-number, encoded in the knotted stucture of the pion field.
Relation to baryon current
Explicitly, the baryon current is the Wess-Zumino-Witten term in the exponentiated pion field (Witten 83a, Witten 83b):
Here the expression in the first line uses the fact that SU(2) is a matrix group, while the second line exporesses the same via pullback of the Maurer-Cartan form from the group manifold.
Relation to Skyrmions
The skyrmion-model (see there) realizes baryons as solitons/instantons in the exponentiated pion field.
Related concepts
References
General
Introduction and survey:
-
Rupert Machleidt, David Rodríguez Entem, Chiral effective field theory and nuclear forces, Phys. Rept. 503:1-75, 2011 (arXiv:1105.2919, doi:10.1016/j.physrep.2011.02.001)
-
Brambilla et al., Section 3.2.7 of: QCD and strongly coupled gauge theories - challenges and perspectives, Eur Phys J C Part Fields. 2014; 74(10): 2981 (arXiv:1404.3723, doi:10.1140/epjc/s10052-014-2981-5)
See also
- Wikipedia, Pion
Decays and interactions
On :
-
Ruvi Aviv, Anthony Zee, Low-Energy Theorem for Phys. Rev. D 5, 2372 (1972) (doi:10.1103/PhysRevD.5.2372)
-
Edward Witten, Global aspects of current algebra, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 422-432 (doi:10.1016/0550-3213(83)90063-9)
-
M. Benayoun, P. David, L. DelBuono, O. Leitner, A Global Treatment Of VMD Physics Up To The : I. Annihilations, Anomalies And Vector Meson Partial Widths, Eur. Phys. J. C65:211-245, 2010 (arXiv:0907.4047)
On pion-nucleon interaction:
- E. Ruiz Arriola, J. E. Amaro, R. Navarro Perez, Three pion nucleon coupling constants, Modern Physics Letters A Vol. 31, No. 28, 1630027 (2016) (arXiv:1606.02171)
On the Dalitz decay of the pion:
-
Richard Dalitz, On an alternative decay process for the neutral -meson, Proceedings of the Physical Society. Section A 64 (7), 667, 1951 (doi:10.1088/0370-1298/64/7/115)
-
Karol Kampf, Marc Knecht, Jiri Novotny, Some aspects of Dalitz decay , presented at Int. Conf. Hadron Structure ‘02, September 2002, Slovakia (arXiv:hep-ph/0212243)
-
Karol Kampf, Marc Knecht, Jiri Novotny, The Dalitz decay revisited, Eur. Phys. J. C46:191-217, 2006 (arXiv:hep-ph/0510021)
-
Henning Berghäuser, Investigation of the Dalitz decays and the electromagnetic form factors of the and -meson, 2010 (spire:1358057)
-
M. Kunkel, Dalitz Decays of Pseudo-Scalar Mesons, talk at Light Meson Decays Workshop August 5, 2012 (pdf)
-
Sergi González-Solís, Single and double Dalitz decays of , and mesons, Nuclear and Particle Physics Proceedings Volumes 258–259, January–February 2015, Pages 94-97 (doi:10.1016/j.nuclphysbps.2015.01.021)
-
Esther Weil, Gernot Eichmann, Christian S. Fischer, Richard Williams, section III.A of: Electromagnetic decays of the neutral pion, Phys. Rev. D 96, 014021 (2017) (arXiv:1704.06046)
Exponentiated pion field and Skyrmions
Discussion of the exponentiated pion field (“chiral field”) in chiral perturbation theory and the interpretation of its winding number as Skyrmion-number / baryon
-
Edward Witten, Global aspects of current algebra, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 422-432 (doi:10.1016/0550-3213(83)90063-9)
-
Edward Witten, Current algebra, baryons, and quark confinement, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 433-444 (doi:10.1016/0550-3213(83)90064-0)
-
Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
(beware that the two copies of the text at these two sources differ!)
-
Mannque Rho et al., Introduction, In: Mannque Rho et al. (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Via holographic QCD
Discussion via the AdS/QCD correspondence:
-
Domenec Espriu, Alisa Katanaeva, Effects of bulk symmetry breaking on AdS/QCD predictions (arXiv:2001.08723)
-
Xuanmin Cao, Matteo Baggioli, Hui Liu, Danning Li, Pion dynamics in a soft-wall AdS-QCD model [arXiv:2210.09088]
Last revised on October 19, 2022 at 04:10:35. See the history of this page for a list of all contributions to it.