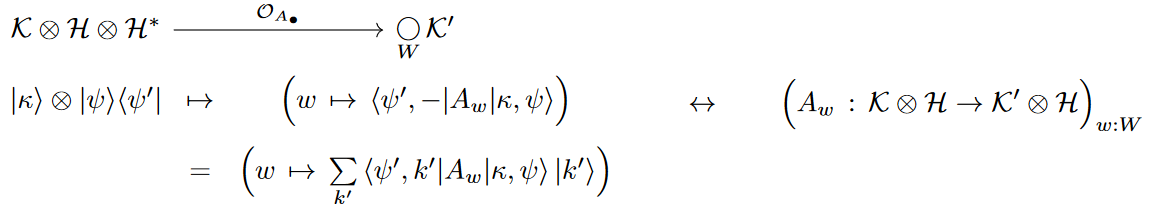Redirected from "I. Moerdijk".
Contents
Context
Categorical algebra
Quantum systems
Contents
Idea
The state monads and costate comonads (store comonads) are typically discussed on cartesian closed categories — but, of course, the analogous construction exists on any closed monoidal category.
An immediate non-cartesian example is a category of vector spaces. At least for a finite-dimensional vector space (and generally on a compact closed category), the linear -state/store (co)monads merge into a single Frobenius monad (see below) which reflects some core structure of open quantum systems (mixed states, quantum channels and their quantum observables).
Due to this fact and the general broad identification of (multiplicative) linear logic with a form of quantum logic, the linear (co)state (co)monad may deserve to be called the quantum state monad (cf. the similar situation for the quantum reader monad).
For example, unitary quantum channels turn out to be embodied by monad transformations between such quantum state monads, so that with this terminology the plausible and desireable statement “quantum channels are quantum state transformations” becomes an actual theorem (see below).
Preliminaries
For definiteness (only), we consider the category of complex vector spaces with, as usual:
Throughout the following we fix
(2)
a finite-dimensional complex vector space.
But most or all of the following discussion works for replaced by any symmetric monoidal closed category and taken from a compact closed subcategory.
In this vein, for notational purposes only (at this point) we choose on :
-
a Hermitian inner product , hence consider it as a finite-dimensional Hilbert space and use bra-ket notation to denote the generic elements of by
and those of its linear dual space
by
-
an orthonormal linear basis , hence such that
(3)
(Kronecker delta).
Furthermore, for , we leave the tensor product-symbol implicit in
In this bra-ket-notation, the compact closure for finite-dimensional (see there) is witnessed by the following isomorphism
(4)
Definition
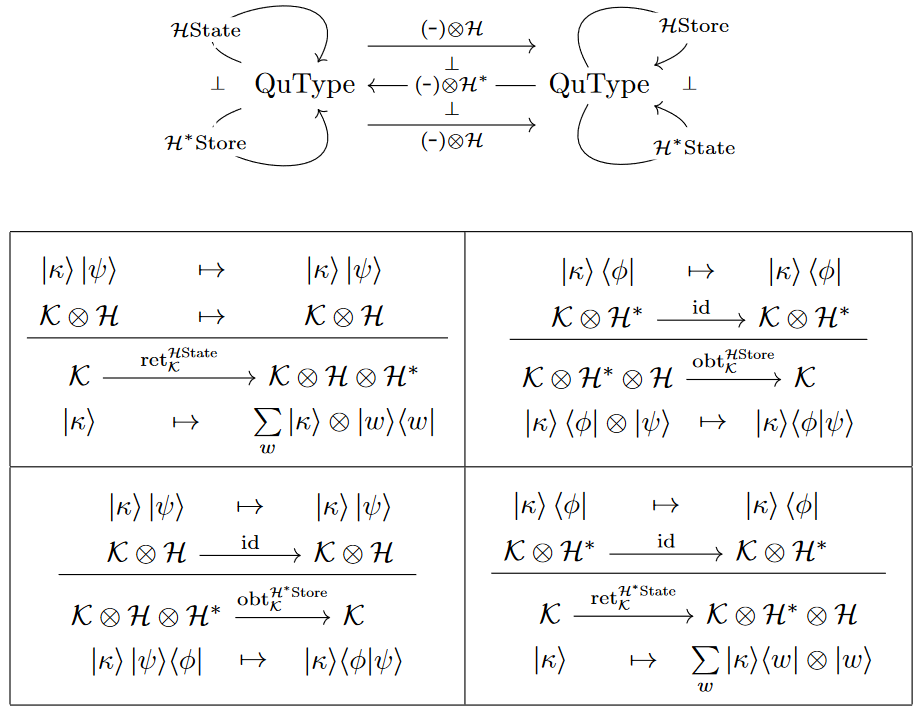
For a finite-dimensional Hilbert space — or generally an object in a compact closed category — its internal hom-adjunction is ambidextrous and associated to a pair of Frobenius monads, in linear version of the classical state monads/store comonad-construction:
Moreover, these (co)monads may equivalently be understood as the (co-)writer monads induced by the endomorphism algebra , which is a Frobenius algebra (by general arguments as recalled in Lauda 2006, made explicit for instance in Vicary 2011 Lem 3.17) and as such makes its (co-)writer monad into a Frobenius monad.
We next spell this out in more detail
(Beware that there is now a switch in conventions. Will streamline later.)
The defining adjunction
The internal hom-adjunction for (2)
(5)
the -unit is:
(6)
Using the symmetric braiding, an orthonormal basis (3) and the compact closure (4) we may equivalently write this as the “insertion of an identity” in the form known from quantum mechanics textbooks:
The adjunction counit is the evaluation map:
(7)
which — again using the symmetric braiding, an orthonormal basis (3) and the compact closure (4) — is equivalently the partial trace over :
(8)
The linear state monad
The adjunction (5) induces a linear version of the state monad:
The underlying endofunctor is
(9)
The join operation is induced from the adjunction counit (8) as:
The linear store comonad
The adjunction (5) induces a linear version of the costate comonad:
The underlying endofunctor is
(10)
The duplication (cojoin) operation in the -CoState comonad (?) is induced from the adjunction unit (6) as follows:
(11)
Finally, the obtain-operation (the comonad counit) is the adjunction counit (8)
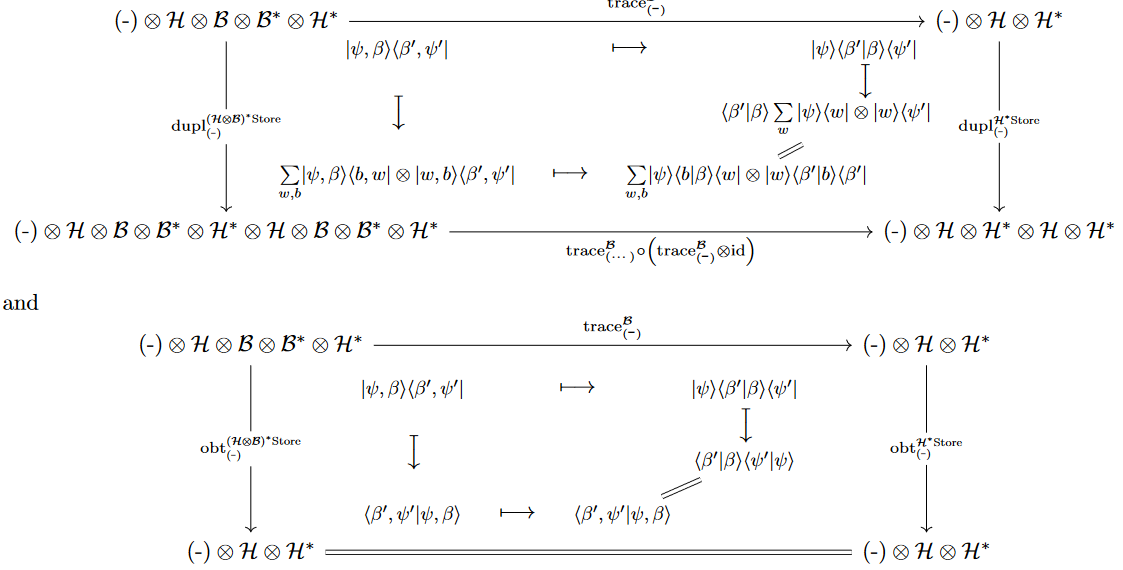
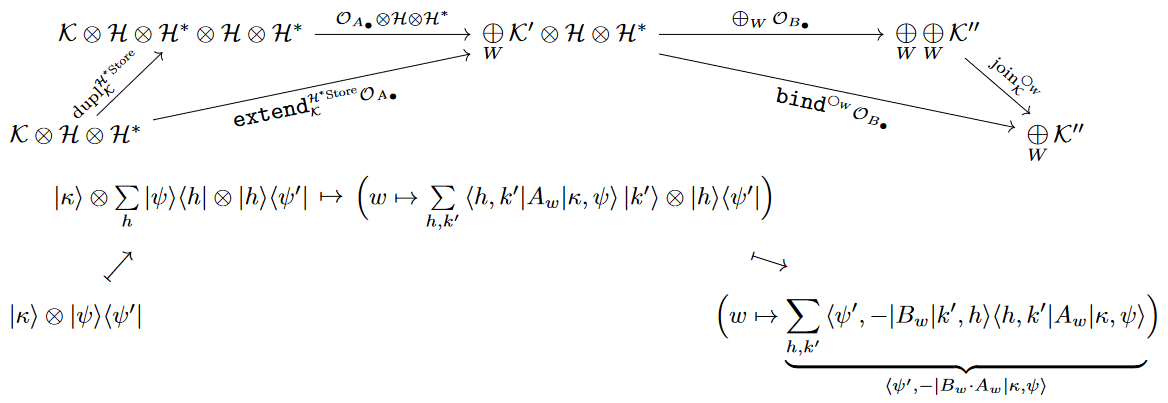
Kleisli structure
We assume an ambient compact closed category such as that of finite-dimensional vector spaces.
For the formula in Prop. to come out naturally, we take – without loss of generality – the generic object on which to apply the linear store comonad to be a dual object .
Proposition
The Kleisli composition on Kleisli morphisms (12) of the quantum store comonad is given by the plain composition of the linear duals of the corresponding superoperators (14):
(16)
Here for
and
we denote their tensor product as
Proof
The relation between a Kleisli morphism (13) and the corresponding super-operator (14) on matrices is
With this and the cojoin operation (11) it follows that the extend-operation turns into
hence
(17)
This implies the claim (16).
The same argument applies with the second copy of replaced by some : The Kleisli category is the opposite of that of superoperators of the form
Examples
Quantum observables are the Quantum state contextful scalars
(The following now starts out a little repetitive, recalling a special case of the general statement above. Will streamline…)
For the classical costate comonad on a cartesian closed category its value and its operations on the tensor unit (the terminal object in this case) are vacuous. Quite in contrast, the linear CoState comonad on the tensor unit encodes core structure of quantum physics:
Proposition
Composition of quantum observables , (18) in the coKleisli category is given by ordinary composition of the corresponding linear operators:
Proof
From (11) we find that the extension operation is given as follows:
hence
Proof
By direct unwinding of the definitions, we find that the counit is respected
by the property that is a left inverse to ,
and the unit is respected
because is also a right inverse to , using here the compact closure identification
(19)
Therefore also the join and cojoin are preserved, eg.:
Proof
Since the structure maps of the -comonad are tensor products of structure maps of and , it is sufficient to show this for the tensor unit, hence for the case that . But in this case , which is a comonadic transformation (in fact the terminal one) by this example).
Alternatively, onee readily checks the required conditions explicitly:
Heisenberg evolution is action of Quantum state transformations
namely on the quantum-state contextful scalars:
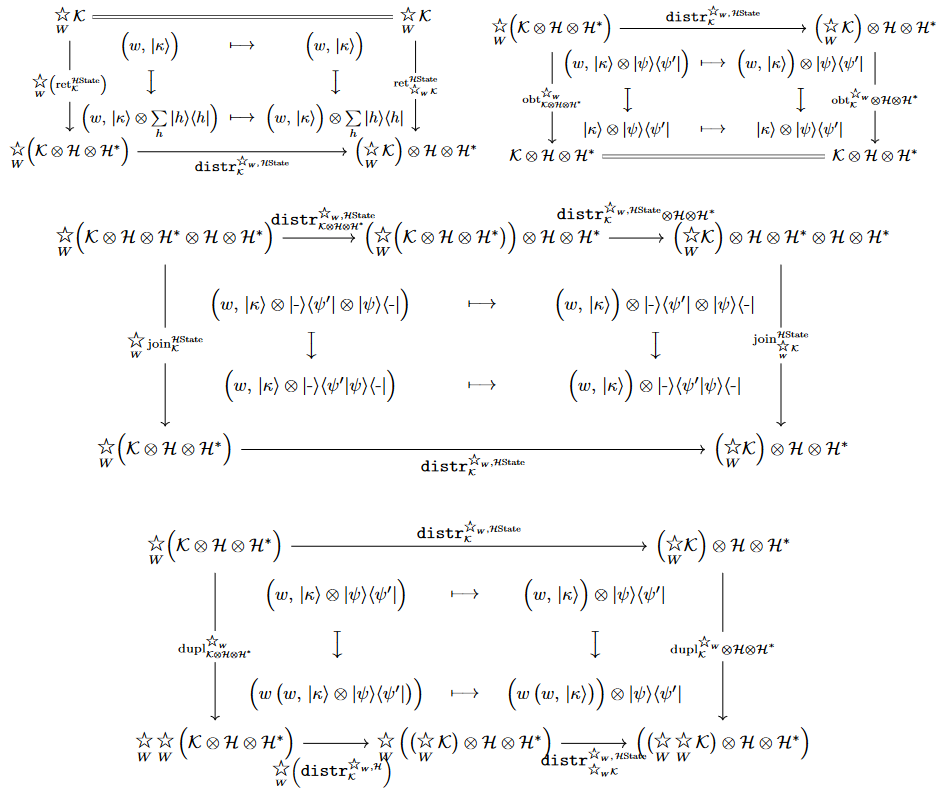
Properties
Interaction with QuantumEnvironment monad