nLab QRAM

This entry is about QRAM in the sense of Giovanetti et al. 2008. For the other sense of classically controlled quantum computation see there.

---

Idea

In quantum computing and quantum information theory, the notion of quantum random access memory (QRAM, due to Giovanetti, Lloyd & Maccone 2008) is meant to be the quantum-analog of the classical notion of random access memory; the key point being that QRAM may be addressed by quantum superpositions of address values and then reads/writes the corresponding quantum superposition of quantum data (GLM08, (1)).

Circuit model

The circuit model for QRAM essentially identifies a quantum program

• of nominal type $\mathscr{H} \longrightarrow \mathscr{H}$

• but with access to a QRAM space $QMem$

with a a quantum circuit of type

$$QMem \otimes \mathscr{H} \longrightarrow QMem \otimes \mathscr{H} \,.$$

In the existing literature this is typically stated in terms of concrete examples rather than in abstract generality, see for instance [Arunachalam et al 2015, Fig. 9] or [Park, Petruccione & Rhee 2019, Fig 1] with review in [Phalak, Chatterjee & Ghosh 2023, Fig 4]. A nicely transparent example is given in by quantumcomputinguk.org:

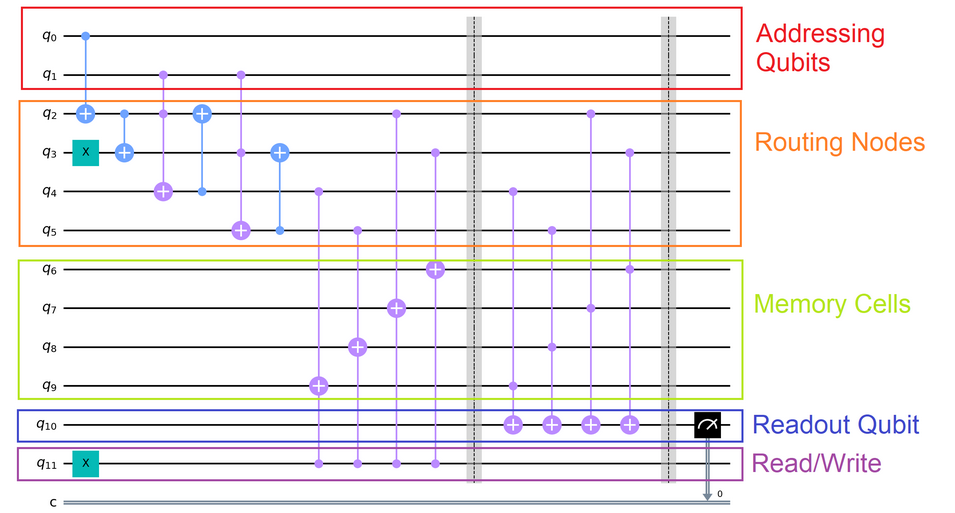
(Here the block “Memory Cells” is our “$QMem$”, the rest is our $\mathscr{H}$.)

This quantum circuit is such that (assuming $q_2 =\cdots = q_6 = 0$)

• if the Read/Write flag is 0 then

  it keeps all qbits (except for “Routing” and) except that the “Readout QBit” is set to one of the four “Memory values” depending on the four possible values of the “Addressing QBits”

• if the Read/Write flag is 1 then

  it keeps all qbits (except for “Routing” and) except that the “Memory QBit” addressed by the value of the “Addressing QBits” is set to the value of $q_{10}$.

• for a superposition of these inputs it yields the corresponding superposition of outputs.

Via linear state-effects

Recall that a classical random access memory of data type $Mem$ is modeled (in terms of monads in computer science) by the state monad induced from the cartesian internal hom-adjunction

• product$\;$ $Mem \times (-) \;\;\dashv\;\; Maps(Mem, -)$ $\;$function set

namely:

$$RAM(Mem,A) \;\coloneqq\; Maps \big( Mem ,\, Mem \times A \big) \,.$$

(Notice that in concrete applications people often insist that $Mem =$ Bool${}^{\times^n}$, but the conceptual nature of RAM is indifferent to this choice.)

Now, with classical data types (such as bits) replaced by quantum data types (such as qbits), namely by linear types, the analogous internal hom-adjunction is

• tensor product$\;$ $QMem \otimes (-) \;\;\dashv\;\; LinMaps(QMem, - )$ $\;$linear space-of-linear maps

and the corresponding monad is

$$QRAM(Mem, \mathscr{H}) \;\coloneqq\; LinMaps \big( QMem ,\, QMem \otimes \mathscr{H} \big)$$

and it seems clear that this does correspond to the intended behaviour of QRAM (where we are free to set $QMem \coloneqq$ QBit${}^{\otimes^n}$, if desired, which is typically the case in the literature).

In particular, the intended equivalence between the “QRAM model” and the “quantum circuit-model” of quantum computation is just the hom-isomorphism of the linear internal hom-adjunction

$$\Big\{ In \longrightarrow LinMaps \big( QMem ,\, QMem \otimes Out \big) \Big\} \;\;\;\;\;\;\; \leftrightarrow \;\;\;\;\;\;\; \Big\{ In \otimes QMem \longrightarrow Out \otimes QMem \Big\} \,.$$

References

The terminology “quantum random access memory” is due to

• Vittorio Giovannetti, Seth Lloyd, Lorenzo Maccone, Quantum random access memory, Phys. Rev. Lett. 100 160501 (2008) [doi:10.1103/PhysRevLett.100.160501, arXiv:0708.1879]

• Vittorio Giovannetti, Seth Lloyd, Lorenzo Maccone, Architectures for a quantum random access memory, Phys. Rev. A 78 052310 (2008) [doi:10.1103/PhysRevA.78.052310, arXiv:0807.4994]

Further development:

• S. Arunachalam et al., On the robustness of bucket brigade quantum RAM, New Journal of Physics, 17 12 (2015) 123010 [arXiv:1502.03450, doi:10.1088/1367-2630/17/12/123010]

• Park, Petruccione, Rhee, Circuit-Based Quantum Random Access Memory for Classical Data, Scientific Reports 9 3949 (2019) [doi:10.1038/s41598-019-40439-3]

Review:

• Alessandro Luongo, The QRAM, §3.1.1. in: Quantum algorithms for data analysis

• Koustubh Phalak, Avimita Chatterjee, Swaroop Ghosh, Quantum Random Access Memory For Dummies [arXiv:2305.01178]

• Samuel Jaques, Arthur G. Rattew, QRAM: A Survey and Critique [arXiv:2305.10310]

With emhasis on laboratory realization:

• Chenxu Liu, et al., III.C (pp. 18) of: Quantum Memory: A Missing Piece in Quantum Computing Units [arXiv:2309.14432]

With Qiskit:

• Implementing QRAM in Qiskit