nLab quantum superposition

Idea

In quantum theory the state of a physical system is given by a vector in a complex vector space (usually a Hilbert space). This means that given any two states $\psi_1$ and $\psi_2$, their sum, the vector $\psi_1 + \psi_2$, also represents a state. This is called the quantum superposition of the two states.

If these quantum states are thought of as wavefunctions solving a linear differential equation such as the Schroedinger equation, Dirac equation, Klein-Gordon equation or Tomonaga-Schwinger equation, their quantum superposition is an example of the general principle of superposition of solutions to linear differential equations.

The concept of quantum superposition is at the heart of what makes quantum physics peculiar, notably via the phenomenon of entanglement.

The various fundamental quantum physics phenomena at play here may be identified with four modal-units of quantum modal logic (as discussed at quantum circuits via dependent linear types):

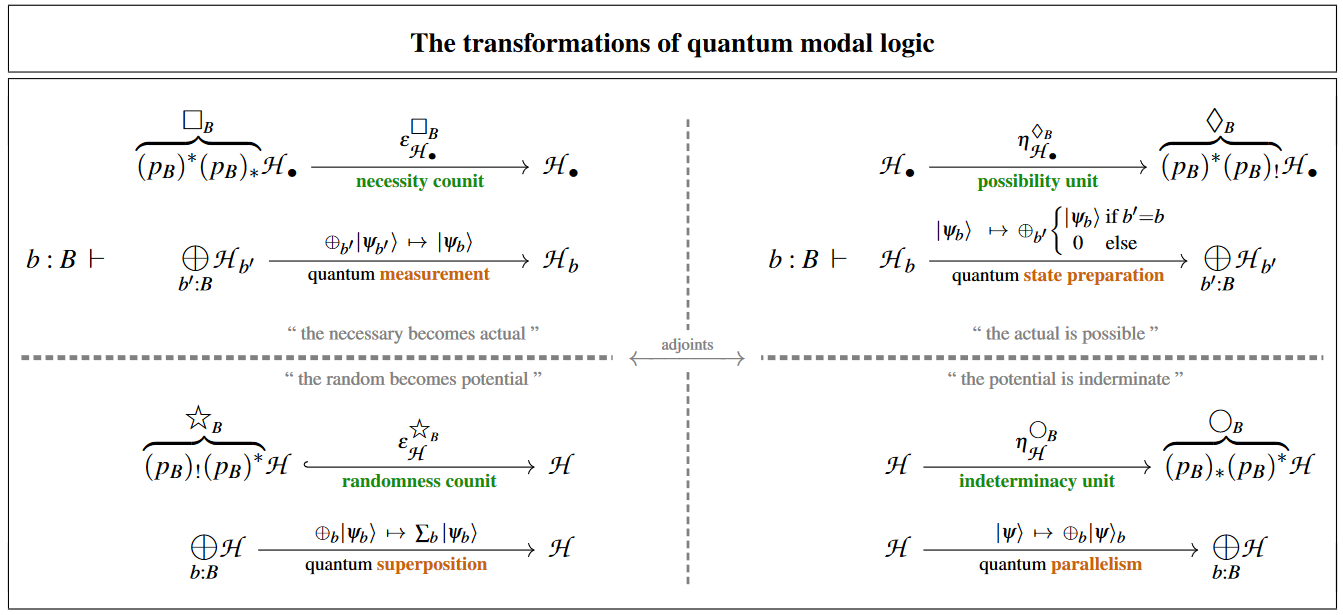
quantum measurement	quantum state preparation
quantum superposition	quantum parallelism

Related concepts

• quantum parallelism

• superposition

quantum probability theory – observables and states

• states

  • classical state

  • quantum state

    • space of states (in geometric quantization)

    • state on a star-algebra, quasi-state

    • qbit, Bell state

      dimer, tensor network state

    • quantum state preparation

    • probability amplitude, quantum fluctuation

    • pure state

      • wave function

      • bra-ket

      • Bell state

    • quantum superposition, quantum interference

    • quantum entanglement

    • quantum measurement

      wave function collapse

      Born rule

      deferred measurement principle

      quantum reader monad

      measurement problem

    • superselection sector

    • mixed state, density matrix

      entanglement entropy

      holographic entanglement entropy

    • coherent quantum state

  • ground state, excited state

  • quasi-free state

  • Fock space, second quantization

  • vacuum, vacuum state

    • Hadamard state

    • vacuum diagram

    • vacuum expectation value, vacuum amplitude, vacuum fluctuation

    • vacuum energy

    • vacuum polarization

    • interacting vacuum

    • thermal vacuum, KMS state

    • vacuum stability

      • false vacuum, tachyon, Coleman-De Luccia instanton

    • theta vacuum

    • perturbative string theory vacuum

      • non-geometric string theory vacuum

      • landscape of string theory vacua

  • entangled state

  • tensor network state

    • matrix product state

    • tree tensor network state

• observables

  • quantum observable, beable

  • algebra of observables, star-algebra

  • Bohr topos

  • quantum operator (in geometric quantization)

  • quantum operation, quantum effect, effect algebra

  • in quantum field theory

    • local observable

    • polynomial observable

      • linear observable

        • field observable

    • regular observable

    • microcausal observable

    • normal-ordered product, time-ordered products, retarded product

    • Wick algebra

    • scattering amplitude

    • interacting field algebra of observables, Bogoliubov's formula

• GNS construction

• theorems

  • order-theoretic structure in quantum mechanics

    • Gleason's theorem

    • Alfsen-Shultz theorem

    • Harding-Döring-Hamhalter theorem

    • Kochen-Specker theorem

    • Nuiten's lemma

  • Wigner's theorem

  • no-cloning theorem

  • Bell's theorem

References

See also

• Wikipedia, Quantum superposition