nLab ADE classification
Context
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Idea
A long list of mathematical structures happens to have a classification that is in bijection with the simply laced Dynkin diagrams of types A, D and E (but excluding type B and C), for instance
-
finitesubgroups of the special orthogonal group and of the special unitary group (see at classification of finite rotation groups) (Milnor 57, see e.g. Keenan 03, theorem 4)
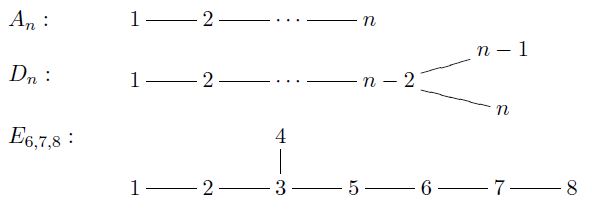
-
connected quivers with a finite number of indecomposable quiver representations over an algebraically closed field
-
7d spherical space forms with spin structure carrying Killing vectors (see at spherical space form – 7d with spin structure)
equivalently: near horizon geometries of smooth (i.e. non-orbifold) BPS black M2-brane-solutions of the equations of motion of 11-dimensional supergravity
This is due to MFFGME 09.
- José Figueroa-O'Farrill et al. 2009 (arXiv:0909.0163, pdf slides)
-
singularities of elliptic fibrations (see there are classification of singular fibers)
-
certain 4d ALE spaces (Kronheimer 89)
-
certain 2d CFTs
-
certain 6d CFTs
-
intersection diagrams of vanishing 2-cycles in K3s (e.g. BBS 07, p.423)
and many more.
ADE classification and McKay correspondence
The obvious question for what might be the conceptual origin of this joint classification is attributed to (Arnold 76).
Starting with (Douglas-Moore 96) is the observation that many of these structures are naturally aspects of the description of string theory KK-compactified on orbifolds with ADE singularities of the form for a finite subgroup of .
Via super Yang-Mills theory
Various seemingly unrelated structures in mathematics fall into an “ADE classification”. Notably finite subgroups of SU(2) and compact simple Lie groups do. The way this works usually is that one tries to classify these structures somehow, and ends up finding that the classification is governed by the combinatorics of Dynkin diagrams (see also McKay correspondence).
While that does explain a bit, it seems the statement that both the icosahedral group and the Lie group E8 are related to the same Dynkin diagram somehow is still more a question than an answer. Why is that so?
The first key insight is due to Kronheimer 89. He showed that the (resolutions of) the orbifold quotients for finite subgroups of are precisely the generic form of the gauge orbits of the direct product group of s acting in the evident way on the direct sum of -s, where and range over the vertices of the Dynkin diagram, and over its edges.
This becomes more illuminating when interpreted in terms of gauge theory: in a quiver gauge theory the gauge group is a direct product group of factors associated with vertices of a quiver, and the particles which are charged under this gauge group arrange, as a linear representation, into a direct sum of -s, for each edge of the quiver.
Pick one such particle, and follow it around as the gauge group transforms it. The space swept out is its gauge orbit, and Kronheimer 89 says that if the quiver is a Dynkin diagram, then this gauge orbit looks like .
On the other extreme, gauge theories are of interest whose gauge group is not a big direct product, but is a simple Lie group, such as SU(N) or E8. The mechanism that relates the two classes of examples is spontaneous symmetry breaking (“Higgsing”): the ground state energy of the field theory may happen to be achieved by putting the fields at any one point in a higher dimensional space of field configurations, acted on by the gauge group, and fixing any one such point “spontaneously” singles out the corresponding stabilizer subgroup.
Now here is the final ingredient: it is N=2 D=4 super Yang-Mills theory (“Seiberg-Witten theory”) which have a potential that is such that its vacua break a simple gauge group such as down to a Dynkin diagram quiver gauge theory. One place where this is reviewed, physics style, is in Albertsson 03, section 2.3.4.
More precisely, these theories have two different kinds of vacua, those on the “Coulomb branch” and those on the “Higgs branch” depending on whether the scalars of the “vector multiplets” (the gauge field sector) or of the “hypermultiplet” (the matter field sector) vanish. The statement above is for the Higgs branch, but the Coulomb branch is supposed to behave “dually”.
So that then finally is the relation, in the ADE classification, between the simple Lie groups and the finite subgroups of SU(2): start with an N=2 super Yang Mills theory with gauge group a simple Lie group. Let it spontaneously find its vacuum and consider the orbit space of the remaining spontaneously broken symmetry group. That is (a resolution of) the orbifold quotient of by a discrete subgroup of .
Related concepts
References
General Surveys
- Vladimir Arnold, Problems in present day mathematics, (1976) in Felix E. Browder, Mathematical developments arising from Hilbert problems, Proceedings of symposia in pure mathematics 28, American Mathematical Society, p. 46, Problem VIII. The A-D-E classifications (V. Arnold).
A survey is in
- Michael Hazewinkel, W Hesseling, Dirk Siersma, and Ferdinand Veldkamp, The ubiquity of Coxeter Dynkin diagrams (an introduction to the ADE problem), Nieuw Archief voor Wiskunde 25 (1977), 257-307. (pdf)
which in turn is summarized in
- Kyler Siegel, The Ubiquity of the ADE classification in Nature , 2014 (pdf)
See also
- Wikipedia, ADE classification
Discussion of the free finite group actions on spheres goes back to
- John Milnor, Groups which act on without fixed points, American Journal of Mathematics Vol. 79, No. 3 (Jul., 1957), pp. 623-630 (JSTOR)
Review inclues
- Adam Keenan, Which finite groups act freely on spheres?, 2003 (pdf)
Discussion of ALE spaces via ADE include
- Peter Kronheimer, The construction of ALE spaces as hyper-Kähler quotients, J. Differential Geom. Volume 29, Number 3 (1989), 665-683. (Euclid)
Related stuff includes…
on immersions of 3-spheres into :
- Shumi Kinjo, Immersions of 3-sphere into 4-space associated with Dynkin diagrams of types A and D (arXiv:1309.6526)
In string theory
The original articles explaining the appearance of ADE classification from within string theory include
-
Michael Douglas, Gregory Moore, D-branes, Quivers, and ALE Instantons (arXiv:hep-th/9603167)
-
Clifford Johnson, Robert Myers, Aspects of Type IIB Theory on ALE Spaces, Phys.Rev. D55 (1997) 6382-6393 (arXiv:hep-th/9610140)
-
Michael Douglas, Brian Greene, David Morrison, Orbifold Resolution by D-Branes, Nucl.Phys. B506:84-106,1997 (arXiv:hep-th/9704151)
-
Brian Greene, Calin Lazaroiu, Mark Raugas, D-branes on Nonabelian Threefold Quotient Singularities, Nucl.Phys. B553 (1999) 711-749 (arXiv:hep-th/9811201)
-
Andrea Cappelli, Jean-Bernard Zuber, A-D-E Classification of Conformal Field Theories (arXiv:0911.3242)
Surveys include
- MO discussion, ADE classification from string theory
Discussion of an ADE-classification of BPS Freund-Rubin compactifications is in
- Paul de Medeiros, José Figueroa-O'Farrill, Sunil Gadhia, Elena Méndez-Escobar, Half-BPS quotients in M-theory: ADE with a twist, JHEP 0910:038,2009 (arXiv:0909.0163, pdf slides)
Specifically the ADE classfication involved in the 6d (2,0)-supersymmetric QFT on the M5-brane is discussed in
-
Edward Witten, Some Comments On String Dynamics (arXiv:hep-th/9507121)
-
Jonathan Heckman, David Morrison, Cumrun Vafa, On the Classification of 6D SCFTs and Generalized ADE Orbifolds (arXiv:1312.5746)
Discussion in the context of M-theory on G₂-manifolds includes
-
Bobby Acharya, section 3.1.1 of M Theory, -manifolds and Four Dimensional Physics, Classical and Quantum Gravity Volume 19 Number 22, 2002 (pdf)
-
Katrin Becker, Melanie Becker, John Schwarz, p. 423 of String Theory and M-Theory: A Modern Introduction, 2007
In solid state physics
On ADE-classifications in/of topological phases of matter/topological order:
- Mayukh Nilay Khan, Jeffrey C. Y. Teo, Taylor L. Hughes, Anyonic Symmetries and Topological Defects in Abelian Topological Phases: an application to the ADE Classification, Phys. Rev. B 90 235149 (2014) arXiv:1403.6478
Last revised on July 18, 2024 at 10:43:19. See the history of this page for a list of all contributions to it.