nLab BMN matrix model
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The BMN matrix model (BMN 02, DSJVR 02) is a deformation of the BFSS matrix model by mass-terms and by a Chern-Simons-term. It arises as the light-cone gauge quantization of the M2-brane not on Minkowski spacetime as for the BFSS matrix model, but on its deformation to a pp-wave spacetime; the mass-terms in the model are proportional to the B-field flux density in the pp-wave vacuum.
Properties
Ground states: and bound states
While the BFSS matrix model notoriously suffers from issues with the definition of its ground state (see there) this problem is fixed in the BMN matrix model by the mass term:
The supersymmetric classical solutions are configurations of fuzzy 2-spheres, corresponding to M2-brane-giant gravitons (BMN 02 (5.4), DSJVR 02, Section 4.2), which under the duality between M-theory and type IIA string theory become D0-D2 brane bound states (Lin04).
In fact, dually these gound states encode also transversal M5-branes and M2-M5 brane bound states, see below.
Relation to black M2/M5-brane backgrounds
The pp-wave spacetime-background for the BMN matrix model arises as the Penrose limit (Inönü-Wigner contraction) of the AdS4x7-sphere near horizon geometry of both the black M2-brane spacetime , as well as the AdS74-sphere near horizon geometry of black M5-branes (BMN 02, Section 2).
Chord diagrams as multi-trace observables in the BMN matrix model
The supersymmetric states of the BMN matrix model are temporally constant complex matrices which are complex metric Lie representations of su(2) (interpreted as fuzzy 2-sphere noncommutative geometries of giant gravitons or equivalently as fuzzy funnels of D0-D2 brane bound states).
A fuzzy 2-sphere-rotation invariant multi-trace observable on these supersymmetric states is hence an expression of the following form:
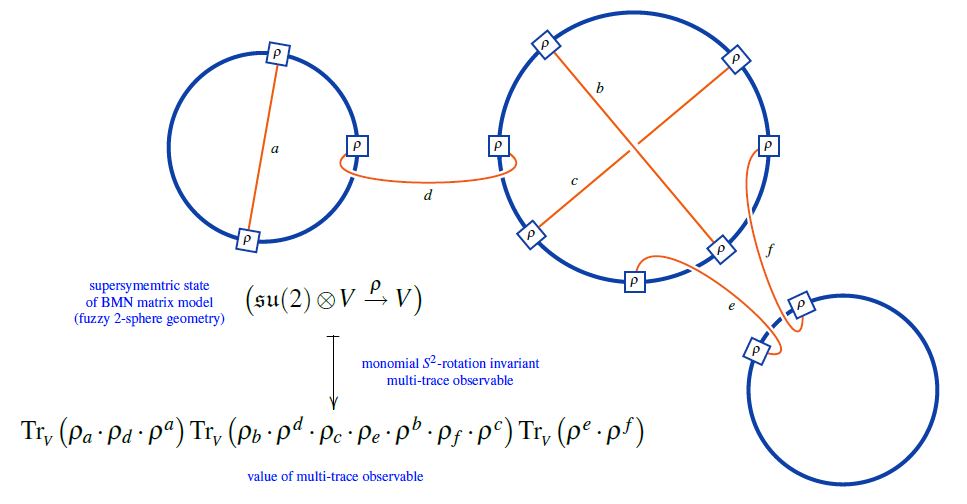
(from Sati-Schreiber 19c)
Here we are showing the corresponding string diagram/Penrose notation for metric Lie representations, which makes manifest that
-
these multi-trace observables are encoded by Sullivan chord diagrams
-
their value on the supersymmetric states is the evaluation of the corresponding Lie algebra weight system on .
Or equivalently, if is a horizontal chord diagram whose -permuted closure is (see here) then the values of the invariant multi-trace observables on the supersymmetric states of the BMN matrix model are the evaluation of on , as shown here:
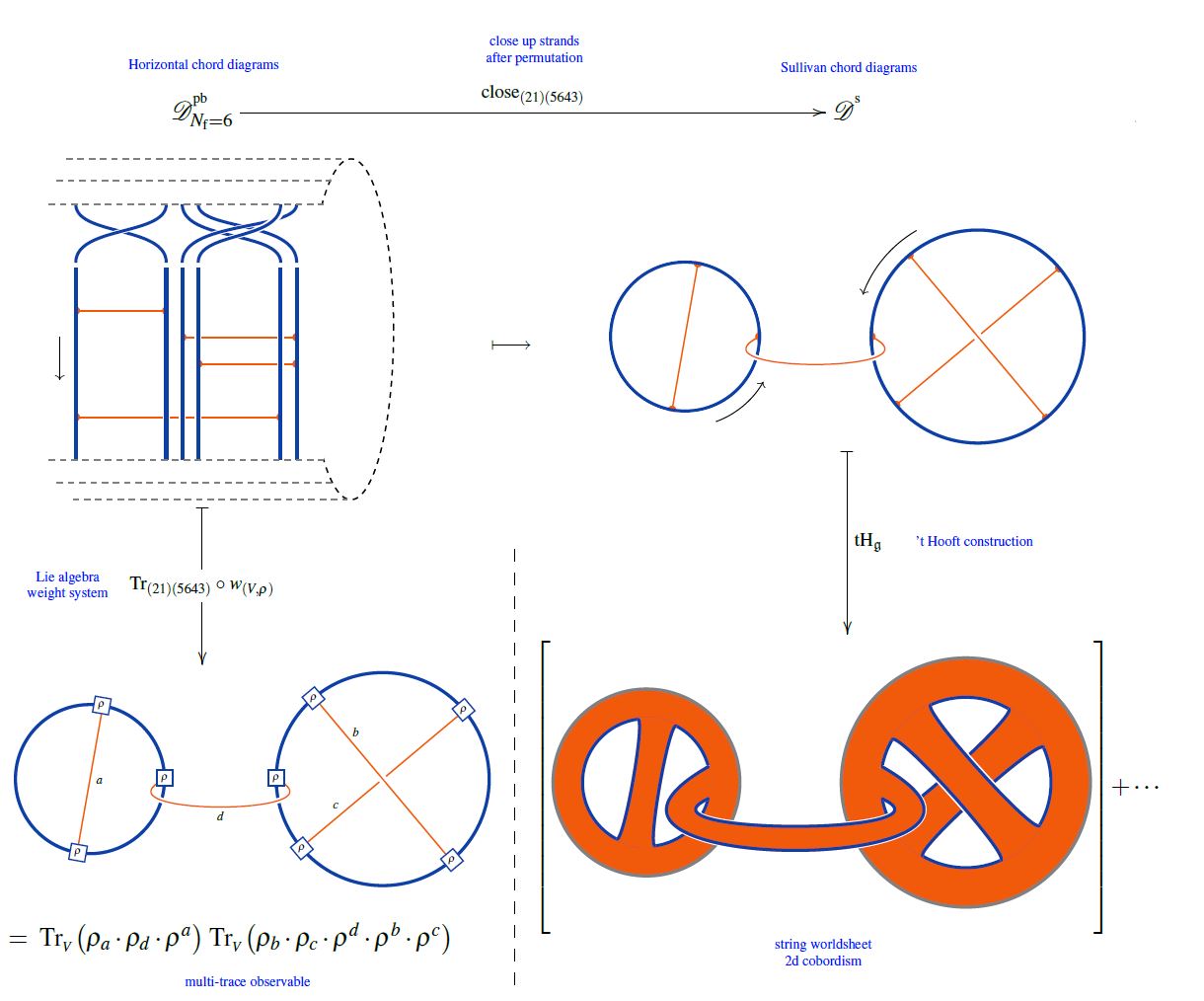
(from Sati-Schreiber 19c)
But since all horizontal weight systems are partitioned Lie algebra weight systems this way, this identifies supersymmetric states of the BMN matrix model as seen by invariant multi-trace observables as horizontal chord diagrams evaluated in Lie algebra weight systems.
M2-M5 brane bound states in the BMN matrix model
There is the suggestion (MSJVR 02, checked in AIST 17a, AIST 17b) that, in the BMN matrix model, supersymmetric M2-M5-brane bound states are identified with isomorphism classes of certain “limit sequences” of longitudinal-light cone-constant -matrix-fields constituting finite-dimensional complex Lie algebra representations of su(2).
Traditional discussion
Concretely, if
denotes the representation containing
of the
(for some finitely indexed set of pairs of natural numbers)
with total dimension
then:
-
a configuration of a finite number of stacks of coincident M5-branes corresponds to a sequence of such representations for which
-
(this being the relevant large N limit)
-
for fixed (being the number of M5-branes in the th stack)
-
and fixed ratios (being the charge/light-cone momentum carried by the th stack);
-
-
an M2-brane configuration corresponds to a sequence of such representations for which
-
(this being the relevant large N limit)
-
for fixed (being the number of M2-brane in the th stack)
-
and fixed ratios (being the charge/light-cone momentum carried by the th stack)
-
for all .
Hence, by extension, any other sequence of finite-dimensional -representations is a kind of mixture of these two cases, interpreted as an M2-M5 brane bound state of sorts.
Formalization via weight systems on chord diagrams
To make this precise, let
be the set of isomorphism classes of complex metric Lie representations (hence finite-dimensional representations) of su(2) (hence of the special linear Lie algebra ) and write
for its linear span (the complex vector space of formal linear combinations of isomorphism classes of metric Lie representations).
Finally, write
for the linear map which sends a formal linear combination of representations to the weight system on Sullivan chord diagrams with chords which is given by tracing in the given representation.
Then a M2-M5-brane bound state as in the traditional discussion above, but now formalized as an su(2)-weight system
hence a weight system horizontal chord diagrams closed to Sullivan chord diagrams, these now being the multi-trace observables on these) is

(from Sati-Schreiber 19c)
Normalization and large limit. The first power of the square root in (1) reflects the volume measure on the fuzzy 2-sphere (by the formula here), while the power of (which is the number of operators in the multi-trace observable evaluating the weight system) gives the normalization (here) of the functions on the fuzzy 2-sphere.
Hence this normalization is such that the single-trace observables among the multi-trace observables, hence those which come from round chord diagrams, coincide on those M2-M5 brane bound states for which , hence those which have a single constitutent fuzzy 2-sphere, with the shape observables on single fuzzy 2-spheres discussed here:

(from Sati-Schreiber 19c)
Therefore, with this normalization, the limits and of (1) should exist in weight systems. The former trivially so, the latter by the usual convergence of the fuzzy 2-sphere to the round 2-sphere in the large N limit.
Notice that the multi trace observables on these states only see the relative radii of the constitutent fuzzy 2-spheres: If then the -dependence of (1) cancels out, reflecting the fact that then there is only a single constituent 2-sphere of which the observable sees only the radius fluctuations, not the absolute radius (proportional to ).
Related concepts
matrix models for brane dynamics:
| D-brane | matrix model |
|---|---|
| D0-brane | BFSS matrix model, BMN matrix model |
| D(-1)-brane | IKKT matrix model |
| D4-brane | nuclear matrix model |
| M-brane | matrix model |
|---|---|
| D2-brane | membrane matrix model |
See also:
References
General
The original articles:
-
David Berenstein, Juan Maldacena, Horatiu Nastase, Sections 5 and Appendix B of: Strings in flat space and pp waves from Super Yang Mills, JHEP 0204 (2002) 013 [arXiv:hep-th/0202021, doi:10.1088/1126-6708/2002/04/013]
(which is otherwise about single trace operators in the AdS/CFT correspondence).
-
Keshav Dasgupta, Mohammad M. Sheikh-Jabbari, Mark Van Raamsdonk: Matrix Perturbation Theory For M-theory On a PP-Wave, J. High Energy Physics 2002 JHEP05 (2002) [arXiv:hep-th/0205185, doi:10.1088/1126-6708/2002/05/056]
-
Nakwoo Kim, Jan Plefka, On the Spectrum of PP-Wave Matrix Theory, Nucl. Phys. B 643 (2002) 31-48 [arXiv:hep-th/0207034]
-
Keshav Dasgupta, Mohammad Sheikh-Jabbari, Mark Van Raamsdonk, Protected Multiplets of M-Theory on a Plane Wave, JHEP 0209:021 (2002) [arXiv:hep-th/0207050, doi:10.1088/1126-6708/2002/09/021]
-
Nakwoo Kim, Jeong-Hyuck Park, Superalgebra for M-theory on a pp-wave, Phys.Rev. D 66 (2002) 106007 [arXiv:hep-th/0207061]
Re-derivation via the superembedding formalism:
- Igor A. Bandos, Multiple M0-brane equations in eleven dimensional pp-wave superspace and BMN matrix model, Phys. Rev. D 85 126005 (2012) [arXiv:1202.5501, doi:10.1103/PhysRevD.85.126005]
Review:
- Badis Ydri, Section 3.10 in: Review of M(atrix)-Theory, Type IIB Matrix Model and Matrix String Theory (arXiv:1708.00734), published as: Matrix Models of String Theory, IOP 2018 (ISBN:978-0-7503-1726-9)
In relation to the Myers effect and D0-D2 brane bound states:
- Hai Lin, The Supergravity Dual of the BMN Matrix Model, JHEP 0412:001, 2004 (arXiv:hep-th/0407250)
Discussion of the large N limit:
- Corneliu Sochichiu, Continuum limit(s) of BMN matrix model: Where is the (nonabelian) gauge group?, Phys.Lett. B574 (2003) 105-110 (arXiv:hep-th/0206239)
Computer simulation (lattice gauge theory):
- Hrant Gharibyan, Masanori Hanada, Masazumi Honda, Junyu Liu, Toward simulating Superstring/M-theory on a quantum computer (arXiv:2011.06573)
and comparison in the large N limit with computations in supergravity:
- S. Pateloudis et al., Precision test of gauge/gravity duality in -brane matrix model at low temperature, J. High Energ. Phys. 2023 71 (2023) [arXiv:2210.04881, doi:10.1007/JHEP03(2023)071]
Analogous mass-deformation of the IKKT matrix model:
-
Shota Komatsu, Adrien Martina, João Penedones, Antoine Vuignier, Xiang Zhao: Einstein gravity from a matrix integral – Part I [arXiv:2410.18173]
-
Shota Komatsu, Adrien Martina, Joao Penedones, Antoine Vuignier, Xiang Zhao: Einstein gravity from a matrix integral – Part II [arXiv:2411.18678]
See also
-
Jens Hoppe. Ki-Myeong Lee, New BPS Configurations of BMN Matrix Theory, JHEP 0806:041, 2008 (arXiv:0712.3616)
-
Masanori Hanada, Lorenzo Mannelli, Yoshinori Matsuo, Four-dimensional super Yang-Mills from matrix model, Phys. Rev. D 80, 125001 (arXiv:0905.2995)
-
Yolanda Lozano, Carlos Nunez, Salomon Zacarias, BMN Vacua, Superstars and Non-Abelian T-duality, JHEP 09 (2017) 008 (arXiv:1703.00417)
-
Yuhma Asano, Samuel Kováčic, Denjoe O’Connor, The Confining Transition in the Bosonic BMN Matrix Model (arXiv:2001.03749)
-
Minos Axenides, Emmanuel Floratos, Dimitrios Katsinis, Georgios Linardopoulos, Cascade of instabilities in the classical limit of the BMN matrix model (arXiv:2109.01088)
-
Shota Komatsu, Adrien Martina, João Penedones, Noé Suchel, Antoine Vuignier, Xiang Zhao, Gravity from quantum mechanics of finite matrices [arXiv:2401.16471]
-
Chi-Ming Chang, Witten index of BMN matrix quantum mechanics [arXiv:2404.18442]
-
Nikolay Bobev, Pieter Bomans, Fridrik Freyr Gautason: Spherical Branes and the BMN Matrix Quantum Mechanics [arXiv:2410.21376]
-
Yoav Zigdon: A Charge Constraint in BMN [arXiv:2506.19924]
Thermodynamics
Discussion of thermodynamics, phase transitions, confinement and thermal field theory of the BMN matrix model:
-
Hyeonjoon Shin, Kentaroh Yoshida, Thermodynamic Behavior of Fuzzy Membranes in PP-Wave Matrix Model, Phys.Lett. B627 (2005) 188-196 (arXiv:hep-th/0507029)
-
Curtis T. Asplund, David Berenstein, Diego Trancanelli, Evidence for fast thermalization in the plane-wave matrix model, Phys. Rev. Lett. 107, 171602 (2011) (arXiv:1104.5469)
-
Lucas Brady, Vatche Sahakian, Scrambling with Matrix Black Holes, Phys Rev D 88, 046003 (2013) (arXiv:1306.5200)
-
Miguel S. Costa, Lauren Greenspan, Joao Penedones, Jorge Santos, Thermodynamics of the BMN matrix model at strong coupling, JHEP 03 (2015) 069 (arXiv:1411.5541)
-
Samuel Pramodh, Vatche Sahakian From Black Hole to Qubits: Evidence of Fast Scrambling in BMN theory, JHEP 7, July 2015, 67 (arXiv:1412.2396)
-
Yuhma Asano, Veselin G. Filev, Samuel Kováčik, Denjoe O’Connor, The non-perturbative phase diagram of the BMN matrix model, JHEP 1807 (2018) 152 (arXiv:1805.05314)
-
Yuhma Asano, Samuel Kováčic, Denjoe O’Connor, The Confining Transition in the Bosonic BMN Matrix Model (arXiv:2001.03749)
Discussion of chaos in the M2-brane physics described by the BMN matrix model:
- Minos Axenides, Emmanuel Floratos, Georgios Linardopoulos, M2-brane Dynamics in the Classical Limit of the BMN Matrix Model, Phys. Lett. B773 (2017) 265 (arXiv:1707.02878)
See also:
Discussion of entanglement and entropy:
- Cameron Gray, Vatche Sahakian, William Warfield, Emergent geometry through quantum entanglement in Matrix theories (arXiv:2103.06941)
KK-compactification from SYM
On the BMN matrix model as a KK-compactification of D=4 N=4 super Yang-Mills theory on the 3-sphere:
- Nakwoo Kim, Thomas Klose, Jan Plefka, Plane-wave Matrix Theory from N=4 Super Yang-Mills on , Nucl. Phys. B671:359-382, 2003 (arXiv:hep-th/0306054)
Using the KK-compactification of D=4 N=4 super Yang-Mills theory to the BMN matrix model for lattice gauge theory-computations in D=4 N=4 SYM and for numerical checks of the AdS-CFT correspondence:
- Masazumi Honda, Goro Ishiki, Sang-Woo Kim, Jun Nishimura, Asato Tsuchiya, Direct test of the AdS/CFT correspondence by Monte Carlo studies of N=4 super Yang-Mills theory, JHEP 1311 (2013) 200 (arXiv:1308.3525)
M5-branes in the BMN matrix model
On light cone transversal M5-branes and M2-M5 brane bound states in the BMN matrix model:
The proposal of passing to horizontal/vertical limits of sizes of partitions is due to:
- Juan Maldacena, Mohammad Sheikh-Jabbari, Mark Van Raamsdonk, Transverse Fivebranes in Matrix Theory, JHEP 0301:038 (2003) arXiv:hep-th/0211139, doi:10.1088/1126-6708/2003/01/038
A detailed check is in:
- Yuhma Asano, Goro Ishiki, Shinji Shimasaki, Seiji Terashima, Spherical transverse M5-branes from the plane wave matrix model, JHEP 02 (2018) 076 arXiv:1711.07681, doi:10.1007/JHEP02(2018)076
Review in:
- Yuhma Asano, Goro Ishiki, Shinji Shimasaki, Seiji Terashima, On the transverse M5-branes in matrix theory, Phys. Rev. D 96 126003 (2017) arXiv:1701.07140, doi:10.1103/PhysRevD.96.126003
In a limit where aspects of little string theory on NS5-branes becomes visible:
-
Hai Lin, Juan Maldacena, Fivebranes from gauge theory, Phys. Rev. D 74 084014 (2006) arXiv:hep-th/0509235, doi:10.1103/PhysRevD.74.084014
-
Henry Ling, Ali Reza Mohazab, Hsien-Hang Shieh, Greg van Anders, Mark Van Raamsdonk, Little String Theory from a Double-Scaled Matrix Model, JHEP 0610:018 (2006) arXiv:hep-th/0606014, doi:10.1088/1126-6708/2006/10/018
-
Yuhma Asano, Goro Ishiki, Takaki Matsumoto, Shinji Shimasaki, Hiromasa Watanabe, On the existence of the NS5-brane limit of the plane wave matrix model, PTEP 2023 (2023) 4, 043B01 arXiv:2211.13716, doi:10.1093/ptep/ptad042
pp-Waves as Penrose limits of spacetimes
Dedicated discussion of pp-wave spacetimes as Penrose limits (Inönü-Wigner contractions) of AdSp x S^q spacetimes and of the corresponding limit of AdS-CFT duality:
-
David Berenstein, Juan Maldacena, Horatiu Nastase, Section 2 of: Strings in flat space and pp waves from Super Yang Mills, JHEP 0204 (2002) 013 (arXiv:hep-th/0202021)
-
N. Itzhaki, Igor Klebanov, Sunil Mukhi, PP Wave Limit and Enhanced Supersymmetry in Gauge Theories, JHEP 0203 (2002) 048 (arXiv:hep-th/0202153)
-
Nakwoo Kim, Ari Pankiewicz, Soo-Jong Rey, Stefan Theisen, Superstring on PP-Wave Orbifold from Large-N Quiver Gauge Theory, Eur. Phys. J. C25:327-332, 2002 (arXiv:hep-th/0203080)
-
E. Floratos, Alex Kehagias, Penrose Limits of Orbifolds and Orientifolds, JHEP 0207 (2002) 031 (arXiv:hep-th/0203134)
-
E. M. Sahraoui, E. H. Saidi, Metric Building of pp Wave Orbifold Geometries, Phys.Lett. B558 (2003) 221-228 (arXiv:hep-th/0210168)
Review:
-
Darius Sadri, Mohammad Sheikh-Jabbari, The Plane-Wave/Super Yang-Mills Duality, Rev. Mod. Phys. 76:853, 2004 (arXiv:hep-th/0310119)
-
Badis Ydri, Section 3.1.10 of: Review of M(atrix)-Theory, Type IIB Matrix Model and Matrix String Theory (arXiv:1708.00734), published as: Matrix Models of String Theory, IOP 2018 (ISBN:978-0-7503-1726-9)
See also:
- Michael Gutperle, Nicholas Klein, A Penrose limit for type IIB solutions (arXiv:2105.10824)
Last revised on June 26, 2025 at 11:01:28. See the history of this page for a list of all contributions to it.