nLab dynamic lifting
Context
Computation
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Quantum systems
-
quantum algorithms:
Contents
Idea
In quantum computation the term “dynamic lifting” (mostly used in the Quipper-community, starting around Green et al (2013), p. 5) refers to the outcome of quantum measurement-results — which can be known only during runtime (ie. “dynamically”), due to the intrinsic stochastic nature of quantum physics — being turned into (ie. “lifted” back to) variables on which subsequent classical computation may be conditioned, which may then in turn control further quantum circuits, etc.:
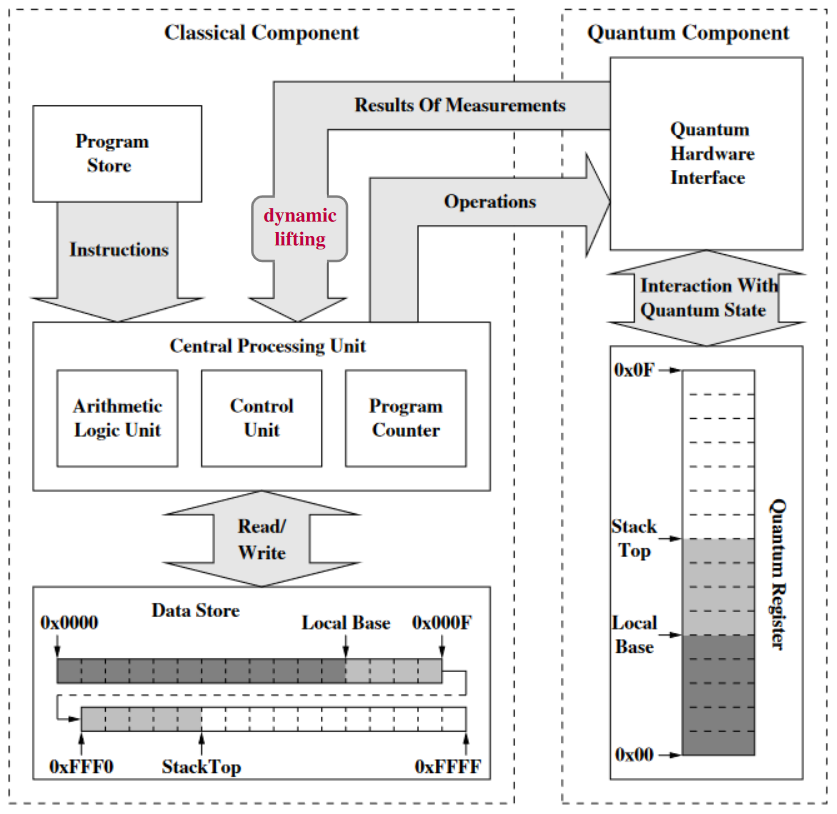
Dynamic lifting is thought (eg. Rand (2018),p. 52) to be optional in cases like the quantum teleportation protocol but necessary for applications like
-
quantum error correction (e.g. Paler, Herr & Devitt (2019), §4.1), where error correction steps are conditioned on quantum measurement of syndrome qbits;
-
repeat-until-success computing, where a quantum circuit is re-run on its input data until a failure syndrome measurement indicates success.
There have been several (partial) proposals for the precise categorical semantics of this idea, see the references below. Another formalization, via monadic effects of potentiality modalities in dependent linear type theory, is discussed at quantum circuits via dependent linear types (CQTS 2022, see there).
References
General
The general but informal idea of quantum computation with classical control that may itself be conditioned on quantum measurement results (see also at Quantum Computation – Classical control and quantum data) may be argued to be implicit already in Knill (1996).
Explicit discussion includes:
- Rajagopal Nagarajan, Nikolaos Papanikolaou, David Williams, Simulating and Compiling Code for the Sequential Quantum Random Access Machine, Electronic Notes in Theoretical Computer Science Volume 170, 6 March 2007, Pages 101-124 [doi:10.1016/j.entcs.2006.12.014]
The term “dynamic lifting” is mainly used in discussion of the quantum programming language Quipper. Its first (brief) appearance might be that in:
- Alexander Green, Peter LeFanu Lumsdaine, Neil Ross, Peter Selinger, Benoît Valiron, p.5 of: Quipper: A Scalable Quantum Programming Language, ACM SIGPLAN Notices 48 6 (2013) 333-342 [arXiv:1304.3390, doi:10.1145/2499370.2462177]
More in-depth discussion of “dynamic lifting” is in:
- Robert Rand, pp. 40 of: Formally Verified Quantum Programming, UPenn (2018) [ediss:3175]
Categorical semantics
Proposals for categorical semantics of “dynamic lifting”, mostly following along the lines of some dependent linear type theory, such as found in Quipper:
-
Mathys Rennela, Sam Staton, Classical Control, Quantum Circuits and Linear Logic in Enriched Category Theory, Logical Methods in Computer Science 16 (2020) lmcs:6192 [arXiv:1711.05159, doi:10.23638/LMCS-16(1:30)2020]
(cf. EWIRE)
-
Dongho Lee, Sebastien Bardin, Valentin Perrelle, Benoît Valiron, Formalization of a Programming Language for Quantum Circuits with Measurement and Classical Control, talk at Journées Informatique Quantique 2019 (Nov 2019) [pdf, pdf]
-
Dongho Lee, Valentin Perrelle, Benoît Valiron, Zhaowei Xu, Concrete Categorical Model of a Quantum Circuit Description Language with Measurement, Leibniz International Proceedings in Informatics 213 (2021) 51:1-51:20 [arXiv:2110.02691, doi:10.4230/LIPIcs.FSTTCS.2021.51]
-
Andrea Colledan, Ugo Dal Lago, On Dynamic Lifting and Effect Typing in Circuit Description Languages, talk at TYPES Workshop, Nantes (2022) [arXiv:2202.07636, pdf, pdf]
-
Peng Fu, Kohei Kishida, Neil J. Ross, Peter Selinger, A biset-enriched categorical model for Proto-Quipper with dynamic lifting, in proceedings of Quantum Physics and Logic 2022 [arXiv:2204.13039]
-
Peng Fu, Kohei Kishida, Neil J. Ross, Peter Selinger, Proto-Quipper with dynamic lifting, in proceedings of Quantum Physics and Logic 2022 [arXiv:2204.13041]
-
Urs Schreiber, Quantum Data Types via Linear HoTT (Nov 2022)
-
Dongho Lee, Formal Methods for Quantum Programming Languages, Paris Saclay (Dec 2022) [hal:tel-03895847]
-
Hisham Sati, Urs Schreiber, The Quantum Monadology [arXiv:2310.15735]
Last revised on November 13, 2023 at 17:36:34. See the history of this page for a list of all contributions to it.