nLab function monad
Context
Categorical algebra
internalization and categorical algebra
-
algebra object (associative, Lie, …)
Mapping space
General abstract
-
hom-set, hom-object, internal hom, exponential object, derived hom-space
-
loop space object, free loop space object, derived loop space
Topology
Simplicial homotopy theory
Differential topology
Stable homotopy theory
Geometric homotopy theory
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Contents
Idea
In a cartesian closed category/type theory , given any object/type there is a monad
given by forming the internal hom out of , hence the “space of functions” out of . This is sometimes called the function monad. Its unit is given by sending values to constant functions with that value, and the monad operation is given by evaluating on the diagonal.
In the context of monads in computer science this monad is called the reader monad or environment monad. It serves to write programs in which all operations may “read in” a state of type (an “environment” variable).
Definition
We first describe the reader monad explicitly
as a monad on Sets.
Then we describe it, more generally as the monad induced by a right base change adjunction
In this form the construction makes more sense generally (see for instance the quantum reader monad).
We write
for the corresponding internal hom. In Sets this is the operation of forming function sets.
Fix .
In components
-
The underlying-functor of the -reader monad is
-
The unit of the monad is given by constructing constant functions:
-
The monad multiplication is given by “evaluating diagonally:
To check that this definition satisfies the monad-axioms:
and
and
Via base change
For , write for the category of -indexed sets of objects of . (More generally, if is a locally cartesian closed category (categorical semantics for dependent type theory), take be the slice category over .)
The right base change adjunction (context extension dependent product) is
Under the evident identification of maps with tuples , the reader monad is the monad induced from this adjunction:
Remark
One may also think of this as being the polynomial functor associated with this span:
Remark
The comonad obtained by composing the other way around, , is the modal operator usually called necessity
From the universal property of the Cartesian product, one finds that:
The adjunction unit is
The adjunction counit is:
The adjunction unit is clearly the monad unit.
The adjunction counit gives the multiplication on the monad:
Properties
Relation to coreader- and state monad
In a cartesian closed category/type theory , the reader monad is right adjoint to the coreader comonad .
The composite of coreader comonad followed by reader monad is the state monad This monad models the situation where a program may not only depend on a immutable parameter but may be allowed to change it.
Just as the coreader comonad canonically becomes a monad when is a monoid, so the reader monad becomes a comonad in that case, and then it is sometimes called the “traced comonad”.
Relation to random variables in probability theory
It makes sense to think of as producing spaces of random variables (Verdier 14) depending on possible worlds [Toronto & McCarthy 10b, slide 24].
(While, from the perspective of modal type theory, its siblings and may be called necessity and possibility, respectively).
The intuition behind the Reader monad, for a mathematician, is perhaps stochastic variables. A stochastic variable is a function from a probability space to some other space. So we see a stochastic variable as a monadic value. [Verdier 14]
you could interpret this by regarding random variables as reader monad computations. [Toronto & McCarthy 10b, slide 35]
Toronto & McCarthy 10a, 2.2, Toronto 14, 6.2 call the function monad the random variable idiom.
This is also brought out by the relation of linear reader algebras to quantum measurement, see below. For more see also at nondeterministic computation the section Via indefiniteness effects.
Free modules over the reader monad
For a set, the Kleisli category for the -reader monad has -tuples of functions as morphisms:
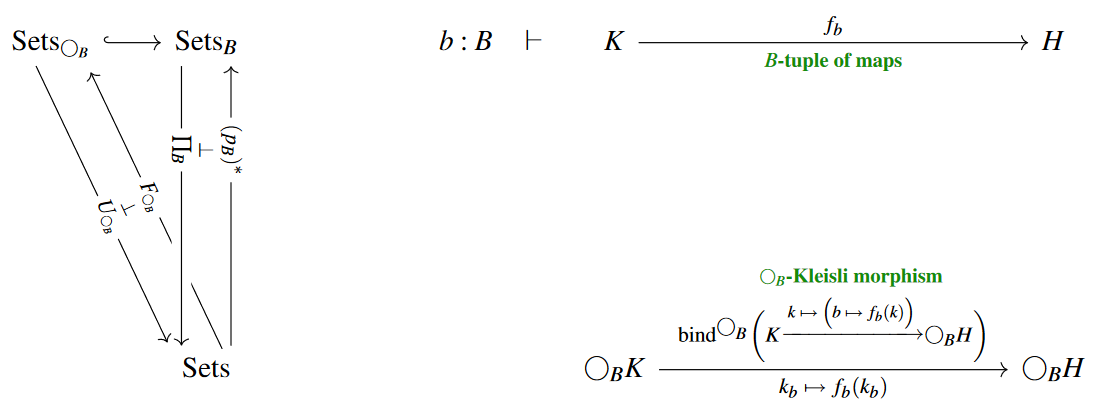
(On the left we are showing the situation of the comparison functor and on the right we are using the “bind”-notation from monads in computer science.)
General modules over the reader monad
In general, the algebras for the function monad are not easily characterizable. (See also MO:a/868317.)
A special case is when is a 2 element set, where the -reader algebras on correspond to idempotent semigroups, also known as rectangular bands.
But the definition of the reader monad makes sense also for other hyperdoctrines such as for dependent linear types: For the resulting “linear” or “quantum” version of the reader monad the situation is different, see below.
Examples
Quantum reader monad
As remarked above, while the -reader monad on toposes such as Set is induced from the base change adjunction as , the functor is not in general a monadic functor, so that -reader-algebras are not in general equivalent to -indexed sets.
However, this situation changes for -readers analogously defined in other hyperdoctrines.
We discuss the example of the reader monad induced by -dependent linear types which have biproducts, such as -indexed sets of vector spaces (these we may think of as “quantum reader monads”, see the discussion at Quantum Modal Logic). We follow CQTS (2022):
Proposition
(quantum -algebras are -dependent linear types)
For FiniteSets, the category of algebras for the -reader monad
on the category Vect of vector spaces (over any given ground field) is equivalent to that of vector bundles over (hence to -indexed sets of vector spaces):
Proof
We state first an abstract proof and then a concrete proof.
Abstractly, observe that Vect has (finite) biproducts (given by the direct sum of vector spaces) which together with the assumption that is finite implies that :
-
is not only a right adjoint but also a left adjoint (hence an ambidextrous adjoint to pullback of vector bundles along ), hence in particular it preserves all colimits;
-
is a conservative functor (since the -components of any morphism of vector bundles over can still be extracted via (co-)projections from their image under forming the biproduct over ).
Therefore the conditions for the monadicity theorem are met (see there), implying that the functor is monadic functor, which in turn implies the claim.
Alternatively, we now check the claim more concretely by unwinding what it means for a vector space to carry -algebra structure and for a linear map between vector spaces to be a homomorphism for this structure:
First observe that the -monad product on a vector space is explicitly given by:
and that a -algebra structure on is a linear map of this form:
Of such maps, the -action property (here) demands that the following two linear maps are equal:
By considering the value of these maps on tuples of vectors which are non-zero only for single elements one finds that the above condition is equivalent to the following condition:
Moreover, the -unit is given by the diagonal map into the biproduct
so that the unitality property (here) of the -algebra structure demands equivalently that the composite
is the identity function on , hence that this system of projection operators is “complete” in that
In summary, this means that for -tuples of linear maps as in (1) to constitute a -module structure is equivalent to them being systems of orthogonal linear projection operators, whose images
span under direct sum:
Such structures, of course, are exactly the images under the right base change of -indexed sets of vector spaces.
Finally, the homomorphism-property on a linear map between the underlying vector spaces of two such -modules demands that the following diagram commutes:
The -indexed components of this condition require that commutes with all these projection operators, in that
But this evidently means that itself is the image under the direct sum-functor
of a -tuple of linear maps between the -indexed component spaces:
This is the defining property of morphisms in and hence shows that -algebra homomorphisms are equivalently morphisms of -indexed sets of vector spaces, hence that the two categories are agree.
Example
(free quantum -algebras and quantum measurement bases)
The free -algebras in Vect are those whose underlying vector space is of the form for any , hence, under the equivalence of Prop. , are those -dependent linear types which happen to assign the same vector space for all .
But homomorphisms of such free -algebras are still allowed to be non-trivially -dependent families of linear maps. This is directly a special case of Prop. but is also immediate under the Kleisli equivalence from observing that -Kleisli morphisms are of the following form:
In quantum information theory the -algebras in complex vector spaces which are free on the tensor unit (the 1-dimensional complex vector space) play the role of (finite dimensional complex vector spaces underlying) Hilbert space of quantum states which are spanned by the set regarded as a “quantum measurement basis”.
For example, the dependent linear type of qbits is the free -algebra spanned by the classical type Bool of bits, reflecting the two canonical quantum measurement-outcomes (, ) of qbits.
Curiously, from this one finds that quantum measurement is exactly indefiniteness handling
where
-
“indefiniteness” is understood as the the effect/modality expressed by the reader monad (see here),
-
“handling” is understood as effect handling in the sense of effect-monads in computer science (see here);
namely:

Notice that this process may be understood as the “dynamic lifting” of quantum measurement-results into the context (here: Bool) of the ambient dependent linear type theory.
For more on this see at quantum circuits via dependent linear types.
This naturally relates to the discussion of quantum measurement via Frobenius algebra-structures which is popular in the context of quantum information theory via dagger-compact categories – as follows:
Remark
(quantum reader monad is Frobenius)
Since the direct sum of vector spaces is a biproduct and using our running assumption that is a finite set, it follows that the underlying functor of the quantum reader monad from Prop. coincides with that of the coreader comonad, and hence that the quantum reader monad is a Frobenius monad (see there).
Remark
(quantum reader monad is special Frobenius writer monad)
Consider the -indexed the direct sum of the ground field with itself as a -algebra and write
for the writer monad corresponding to this monoid object in Vect: The monad which acts by forming the tensor product and whose monad multiplication and unit of a monad are induced from the multiplication and unit in this monoid.
The above proof of Prop. shows at once that this writer monad is isomorphic to the -reader monad:
Now the monad modules over a writer monad are just the ordinary modules over the corresponding monoid, so that
This provides a rather transparent re-derivation of and alternative perspective on Example .
Dually, as in Prop. , the quantum coreader comonad is isomorphic to the coreader comonad corresponding to the coalgebra-structure on .
Hence, as a Frobenius monad (Prop. ), the quantum reader corresponds to regarded as a Frobenius algebra, in fact as a commutative and special Frobenius algebra. In this form the quantum reader monad is prominent in the literature on quantum information theory via dagger-compact categories [Coecke & Pavlović (2008), §1.5.1, Coecke & Paquette (2008), §2.3].

Related concepts
| (co)monad name | underlying endofunctor | (co)monad structure induced by |
|---|---|---|
| reader monad | on cartesian types | unique comonoid structure on |
| coreader comonad | on cartesian types | unique comonoid structure on |
| writer monad | on monoidal types | chosen monoid structure on |
| cowriter comonad | on monoidal types | chosen monoid structure on chosen comonoid structure on |
| Frobenius (co)writer | on monoidal types | chosen Frobenius monoid structure |
References
General
As a monad in computer science:
-
Olivier Verdier, The Reader and Writer Monads and Comonads, 2014
-
Bartosz Milewski §21.2.3 in: Category Theory for Programmers, Blurb (2019) [pdf, github, webpage, ISBN:9780464243878]
-
Tarmo Uustalu, p.22 of: Monads and Interaction Lecture 1 [pdf, pdf], lecture notes for MGS 2021 (2021):
See also:
-
Wikipedia, Environment monad.
-
Neil Toronto, Jay McCarthy, From Bayesian notation to pure Racket, via measuretheoretic probability , in Implementation and Application of Functional Languages, 2010 (web)
-
Neil Toronto, Jay McCarthy, From Bayesian Notation to Pure Racket, talk notes 2010 (pdf)
-
Neil Toronto, Useful Languages for Probabilistic Modeling and Inference, PhD Thesis, 2014 (pdf, slides)
A treatment of opacity in linguistics via the function monad
-
Gianluca Giorgolo, Ash Asudeh, Monads as a Solution for Generalized Opacity, paper
-
Gianluca Giorgolo, Ash Asudeh, Perspectives, Semantics and Pragmatics, vol. 9, paper
On linear types
The quantum reader monad – implicitly, in its incarnation as the -DualWriter monad – is highlighted in the literature quantum information theory via dagger-compact categories as formalizing “classical structures” (namely linear bases for quantum measurement):
-
Bob Coecke, Duško Pavlović, §1.5.1 of: Quantum measurements without sums, in Louis Kauffman, Samuel Lomonaco (eds.), Mathematics of Quantum Computation and Quantum Technology, Taylor & Francis (2008) 559-596 [arXiv:quant-ph/0608035, doi:10.1201/9781584889007]
-
Bob Coecke, Eric Oliver Paquette, §2.3 in: POVMs and Naimark’s theorem without sums, Electronic Notes in Theoretical Computer Science 210 (2008) 15-31 [arXiv:quant-ph/0608072, doi:10.1016/j.entcs.2008.04.015]
-
Bob Coecke, Eric Paquette, Dusko Pavlovic, Def. 2.8 in: Classical and quantum structures (2008) [pdf, pdf]
The account above follows:
- CQTS, Quantum Data Types via Linear HoTT, talk at Workshop on Quantum Software @ QTML 2022 (Nov 2022) [pdf]
Last revised on October 15, 2024 at 19:05:13. See the history of this page for a list of all contributions to it.