nLab electron-photon interaction
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
In quantum electrodynamics the interaction between the Dirac field , whose quanta are electrons, and the electromagnetic field , whose quanta are photons, is encoded by the interaction Lagrangian density
(with notation as as used at A first idea of quantum field theory, see this example).
For a bump function on spacetime thought of as an adiabatically switched coupling constant, the corresponding interaction action functional is the local observable
where in the first line we have the integral over a pointwise product (this def.) of three field observables (this def.), which in the second line we write equivalently as a normal ordered product, by the discusssion at Wick algebra (this def.).
(e.g. Scharf 95, (3.3.1))
The corresponding Feynman diagram is
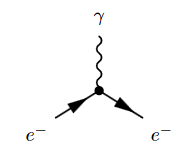
The square of the coupling constant
is called the fine structure constant.
Related concepts
References
Discussion in the context of causal perturbation theory is in
- Günter Scharf, section 3.3 of Finite Quantum Electrodynamics – The Causal Approach, Berlin: Springer-Verlag, 1995, 2nd edition
Last revised on February 12, 2018 at 13:19:28. See the history of this page for a list of all contributions to it.