nLab quantum adiabatic theorem

Idea

In quantum physics, the quantum adiabatic theorem for a parameterized quantum system says that under a sufficiently slow motion of the external parameters along a path $\gamma \,\colon\, [0,1] \to P$ in parameter space $P$, eigenstates for mutually commuting quantum observables of the quantum system at $\gamma(0)$ will approximately evolve to eigenstates at $\gamma(1)$, even if the corresponding eigenvalues change significantly.

For adiabatic transport along a loop, $\gamma(0) = \gamma(1)$, this implies that the eigenspaces of the system are acted on by unitary operators, which (at least for multiplicity/eigen-dimension 1) are known as Berry phases.

The adiabatic parameter-action on ground states of (topologically ordered) quantum materials is one model for quantum computation, see at adiabatic quantum computation. If these adiabatic quantum gates depend only on the isotopy class of the parameter path, then one speaks of topological quantum computation (made explicit in Arovas, Schrieffer, Wilczek & Zee 1985, p. 1, Freedman, Kitaev, Larsen & Wang 2003, pp. 6 and Nayak, Simon, Stern & Freedman 2008, §II.A.2 (p. 6), see also at braiding of anyonic defects).

The following graphics is meant to illustrate this general idea for the case of adiabatic transformation along the braiding of nodal points in the Brillouin torus of semi-metal quantum materials (see the discussion at braid group statistics – anyonic band nodes):

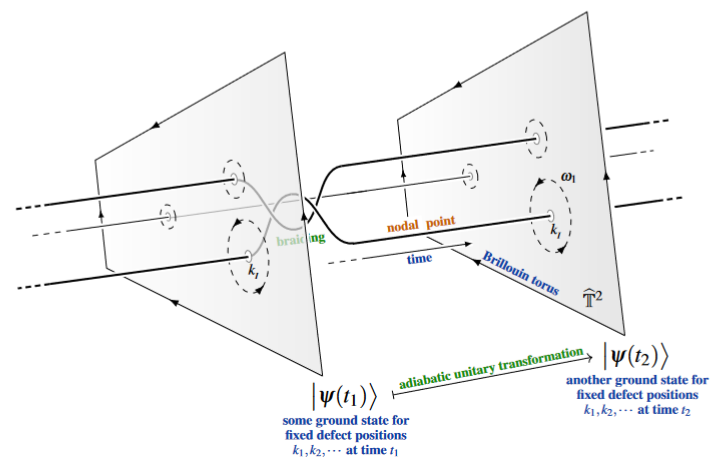
(graphics from SS22)

Related concepts

• Berry connection, Berry phase, Zak phase

• adiabatic

• adiabatic quantum computation

  • anyon

  • braid group statistics

• adiabatic switching

References

General

The original formulation:

• Max Born, Vladimir A. Fock, Beweis des Adiabatensatzes, Zeitschrift für Physik 51 (1928) 165–180 (doi:10.1007/BF01343193)

• Tosio Kato, On the Adiabatic Theorem of Quantum Mechanics, J. Phys. Soc. Jpn. 5 (1950) 435-439 (doi:10.1143/JPSJ.5.435)

• Gheorghe Nenciu, On the adiabatic theorem of quantum mechanics, J. Phys. A: Math. Gen. 13 (1980) L15 [doi:10.1088/0305-4470/13/2/002]

Making explicit the unitary action on degenerate eigenspaces by non-abelian Berry phases:

• Gustavo Rigolin, Gerardo Ortiz, The Adiabatic Theorem for Quantum Systems with Spectral Degeneracy, Phys. Rev. A 85 062111 (2012) [arXiv:1111.5333, doi:10.1103/PhysRevA.85.062111]

See also:

• Wikipedia, Adiabatic theorem

On adiabatic transport subject to repeated quantum measurement:

• Ludmila Viotti, Ana Laura Gramajo, Paula I. Villar, Fernando C. Lombardo, Rosario Fazio, Geometric phases along quantum trajectories [arXiv:2301.04222]

In condensed matter theory

Discussion in solid state physics and in view of gapped topological phases of matter (quantum Hall effect, topological insulators):

• Joseph E. Avron, R. Seiler & L. G. Yaffe, Adiabatic theorems and applications to the quantum Hall effect, Communications in Mathematical Physics 110 (1987) 33–49 [doi:10.1007/BF01209015]

• Joseph E. Avron, A. Raveh, B. Zur, Adiabatic quantum transport in multiply connected systems, Rev. Mod. Phys. 60 (1988) 873-915 [doi:10.1103/RevModPhys.60.873]

• Mathew B. Hastings, Xiao-Gang Wen, Quasiadiabatic continuation of quantum states: The stability of topological ground-state degeneracy and emergent gauge invariance, Phys. Rev. B 72 (2005) 045141 [arXiv:cond-mat/0503554, doi:10.1103/PhysRevB.72.045141]

• Sven Bachmann, Spyridon Michalakis, Bruno Nachtergaele, Robert Sims, Automorphic Equivalence within Gapped Phases of Quantum Lattice Systems, Commun. Math. Phys. 309 (2012) 835-871 [arXiv:1102.0842, doi:10.1007/s00220-011-1380-0]

• Jan Carl Budich, Björn Trauzettel, From the adiabatic theorem of quantum mechanics to topological states of matter, physica status solidi (RRL) 7 1-2 (2013) 109-129 [arXiv:1210.6672, doi:10.1002/pssr.201206416]

• Sven Bachmann, Wojciech De Roeck, Martin Fraas, Adiabatic Theorem for Quantum Spin Systems, Phys. Rev. Lett. 119 (2017) 060201 [doi:10.1103/PhysRevLett.119.060201]

Review:

• Sven Bachmann, Wojciech De Roeck, Martin Fraas, The adiabatic theorem in a quantum many-body setting, in: Analytic Trends in Mathematical Physics, Contemporary Mathematics 741 (2020) 43-58 (arXiv:1808.09985, ISBN:978-1-4704-5388-6)

See also:

• David Aasen, Zhenghan Wang, Matthew B. Hastings, Adiabatic paths of Hamiltonians, symmetries of topological order, and automorphism codes [arXiv:2203.11137]

For topological quantum computation

References which make explicit that the standard model of topological quantum computation by braiding of anyons is a form of adiabatic quantum computation:

• Daniel P. Arovas, Robert Schrieffer, Frank Wilczek, Anthony Zee, Statistical mechanics of anyons, Nuclear Physics B 251 (1985) 117-126 (reprinted in Wilczek 1990, p. 173-182) $[$doi:10.1016/0550-3213(85)90252-4$]$

• Michael Freedman, Alexei Kitaev, Michael Larsen, Zhenghan Wang, pp. 6 of Topological quantum computation, Bull. Amer. Math. Soc. 40 (2003), 31-38 (arXiv:quant-ph/0101025, doi:10.1090/S0273-0979-02-00964-3, pdf)

• Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, Sankar Das Sarma, §II.A.2 (p. 6) of: Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80 1083 (2008) $[$arXiv:0707.1888, doi:10.1103/RevModPhys.80.1083$]$

• Meng Cheng, Victor Galitski, Sankar Das Sarma, Non-adiabatic Effects in the Braiding of Non-Abelian Anyons in Topological Superconductors, Phys. Rev. B 84 (2011) 104529 $[$arXiv:1106.2549, doi:10.1103/PhysRevB.84.104529$]$

• Chris Cesare, Andrew J. Landahl, Dave Bacon, Steven T. Flammia, Alice Neels, Adiabatic topological quantum computing, Phys. Rev. A 92 (2015) 012336 $[$arXiv:1406.2690, doi:10.1103/PhysRevA.92.012336$]$