nLab ER = EPR
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Quantum systems
-
quantum algorithms:
Contents
Idea
The symbols ER = EPR (pronounced: “ee arr is ee pee arr”) serve as a slogan for a hypothesis about quantum gravity, claiming, somewhat vaguely, that entangled particles (the Einstein-Podolsky-Rosen phenomenon: “EPR”) “are” connected by a wormhole (Einstein-Rosen bridge: “ER”).
This slogan is due to Maldacena & Susskind (2013) (there motivated from a search for a solution for the perceived black hole firewall problem) but the idea may in this form have circulated earlier [cf. Verlinde & Verlinde (2022)]. In fact, what is arguably a precise and provable version of the statement (in lattice models) has appeared years earlier: the Ryu-Takayanagi formula, see below (which, however, applies in a holographic context, a qualification not necessarily brought out by Maldacena & Susskind).
At face value the statement “ER = EPR”, even if parsed benevolently, suffers from a typing error between quantum physics and classical gravity. However, like with a Zen koan, one may imagine the paradoxical formulation to propel the intuitive grasp of indeed rather deep principles of holography and particularly of holographic entanglement entropy, such as expressed with precision by the Ryu-Takayanagi formula.
Another source of fun with the slogan “ER = EPR” is to thereby see the two classical and seminal papers by Albert Einstein et al. from 1935 [Einstein & Rosen (1935), Einstein, Podoldsky & Rosen (1935)] — which to Einstein must have seemed unrelated — to secretly be about two sides of the same medal.
As a slogan for the Ryu-Takayanagi formula
The idea meant to be expressed by the slogan “ER = EPR” may usefully be compared to – and may be a way of turning into prose – the Ryu-Takayanagi formula [Ryu & Takayanagi (2006)] (which has a more well-defined content as a theorem in a class of discrete tensor network-models). The RT-formula equates:
- (quantum entanglement:) the entanglement entropy of a boundary quantum field theory in a subspace of an asymptotic boundary
with
- (global spacetime structure:) the minimal area of a cobounding hypersurface in an ambient curved bulk spacetime.
Concretely, in tensor network-models of AdS2/CFT1 duality, the entanglement entropy of any Majorana dimer code-tensor network state turns out to count the number of dimers that cross between a (connected) subregion and its complement:
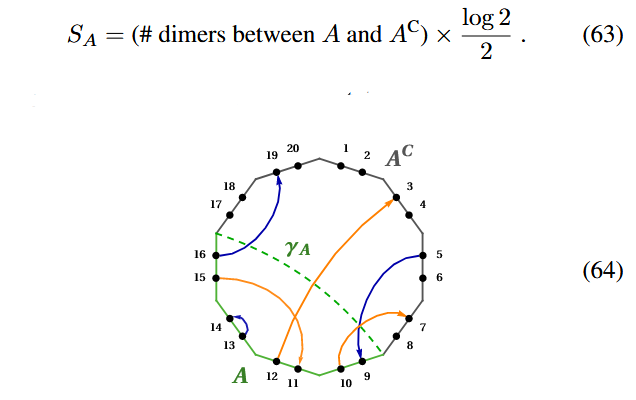
In the case that the dimers correspond to the hyperbolic tesselation from the HaPPY code, this entropy formula
recovers the Ryu-Takayanagi formula (JGPE 19 (78)), as here the number of chords crossing any hyperbolic geodesic grows linearly with the length of this geodesic.
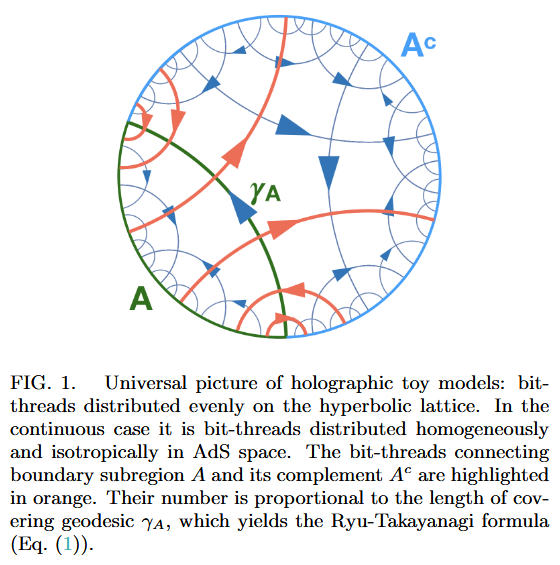
A precursor to this picture is the “bit-thread”-interpretation of entanglement entropy due to Freedman & Headrick 16 (notice the use of “EPR pair” in their Figure 4.)
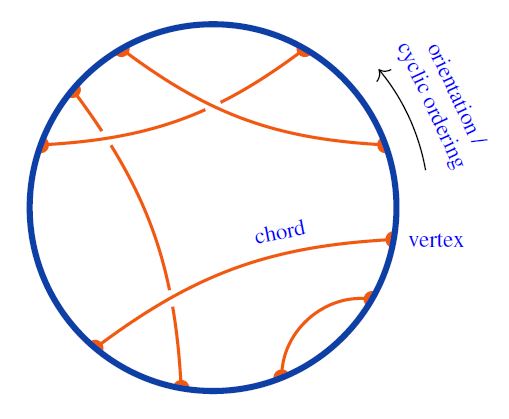
Following Sati-Schreiber 19c we recognize the above Majorana dimer/bit-thread networks from JGPE 19, Yan 19 as chord diagram-encodings of holographic bulks (p. 38).
Notice that the formula for the entanglement entropy in the Majorana dimer code holds generally, for any configuration and hence any underlying chord diagram.
In conclusion, note how each chord here reflects at the same time:
-
(ER) one entangled pair of qbits in the boundary quantum system;
-
(EPR) a geodesic through the hyperbolic plane bulk spacetime,
which is a (rigorous) state of affairs clearly reminiscent of the “ER = EPR” slogan (except that wormholes are replaced by minimal area hypersurfaces, here: geodesics).
For more on this see at holographic entanglement entropy.
Related entries
References
The original result of the Ryu-Takayanagi formula:
- Shinsei Ryu, Tadashi Takayanagi, Holographic Derivation of Entanglement Entropy from AdS/CFT, Phys. Rev. Lett. 96 181602 (2006) [arXiv:hep-th/0603001, doi:10.1103/PhysRevLett.96.181602]
The slogan “ER = EPR” is due to:
-
Juan Maldacena, Leonard Susskind, Cool horizons for entangled black holes, Fortsch. Phys. 61 (2013) 781-811 [arXiv:1306.0533, doi:10.1002/prop.201300020]
-
Leonard Susskind, ER=EPR, GHZ, and the consistency of quantum measurements, Fortsch. Phys. 64 1 (2016) 72-83 [arXiv:1412.8483, doi:10.1002/prop.201500094]
An email exchange of similar content that happened half a year earlier is recalled in:
- Erik Verlinde, Herman Verlinde, A Conversation on ER = EPR [arXiv:2212.09389]
See also
- Wikipedia, ER=EPR
Last revised on July 13, 2023 at 17:06:00. See the history of this page for a list of all contributions to it.