nLab !-modality
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Modalities, Closure and Reflection
Foundations
The basis of it all
Set theory
- fundamentals of set theory
- material set theory
- presentations of set theory
- structuralism in set theory
- class-set theory
- constructive set theory
- algebraic set theory
Foundational axioms
-
basic constructions:
-
strong axioms
-
further
Removing axioms
Contents
Idea
In full linear logic [Girard 1987] and more generally in linear type theory there is assumed a (comonadic) modality traditionally denoted “!” whose role is to model the “underlying” classical (intuitionistic) type of a given linear type.
This is alternatively called the “exponential modality” (for good reasons discussed below), or “storage modality” (as it allows to duplicate and hence “store” otherwise linear data) and sometimes pronounced “of course” (intended alongside “necessarily” and “possibly” as used in modal logic) or even “bang” (just in reference to the symbol “!”).
In classical linear logic (meaning with involutive de Morgan duality), the de Morgan dual of “!” is denoted “?” and then sometimes pronounced “why not”.
Today it is understood (cf. Melliès 2009, p. 36) that the exponential modality is best and generally to be thought as as, first of all a comonad on linear types (Seely 1989 §2, dePaiva 1989, Benton, Bierman, de Paiva and Hyland 1992) which, secondly, is induced by an adjunction to classical (meaning here: non-linear intuitionistic) types with special monoidal properties (Seely 1989 §2, Bierman 1994 pp. 157, Benton 1995).
In a most elementary and illuminating example (which may not have received the attention it deserves, cf. the history at quantum logic):
-
classical intuitionistic types form (are interpreted in) the category of Sets
-
linear types form (are interpreted in) the category of vector spaces (cf. Murfet 2014)
and the adjoint functors in question are
-
forming the linear span of a set
-
forming the underlying set of a vector space:
in which case the exponential modality acts by sending a vector space to the linear span of its underlying set
One sees that this construction takes (direct) sums to (tensor) products
and zero (objects) to unit (objects)
as expected of any exponential map, whence the name “exponential modality”.
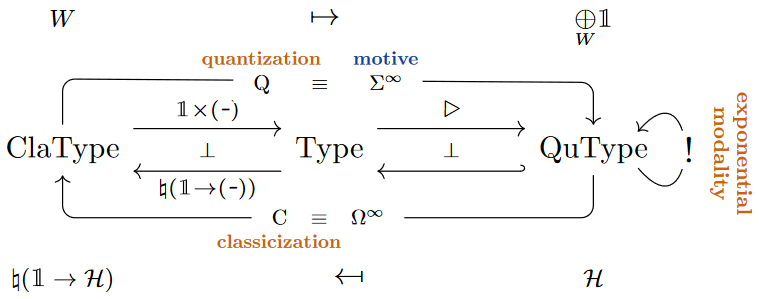
This example is the 0-sector of the more famous stabilization (-)adjunction between (the homotopy theory of) topological spaces and (the stable homotopy theory of) module spectra equipped with the symmetric smash product of spectra (given by forming suspension spectra ), which points to a deeper origin of the “exponential modality”, see below and at linear homotopy type theory for more on this.
Categorical semantics
Following Seely 1989, dePaiva 1989, Benton, Bierman, de Paiva and Hyland 1992 it is common convention that “!” should be a comonad on the type system (and ? should be a monad, see also at monads in computer science), but there is some room in which further axioms to impose. The goal is to capture the syntactic rules allowing assumptions of the form to be duplicated and discarded.
Intuitionistic case
The definition from Seely, adapted to the intuitionistic case and modernized, is:
Definition
Let be
- a cartesian monoidal category, with Cartesian product “” and tensor unit the terminal object .
which in addition carries the structure of
- a symmetric monoidal category with respect to a tensor product with tensor unit .
A Seely comonad on is a comonad that is a strong monoidal as a functor from cartesian monoidal structure to the other monoidal structure :
meaning that there are natural transformations of the form
and
(There is also an additional coherence axiom that should be imposed; see Melliès 2009, section 7.3.)
Remark
(the exponential condition)
In linear logic, the cartesian monoidal structure on linear types is often denoted “” (“additive conjunction”), in which case the condition (1) reads
But in key examples of categories of (the multiplicative fragment of) linear logic (such as Vect, cf. Murfet 2014), the cartesian product is actually a biproduct, hence a direct sum, in which case the condition on the exponential modality is that
it takes (direct) sums to (tensor) products
it takes zero (objects) to unit (objects)
as befits any exponential map and may explain the choice of terminology here.
This condition implies that the Kleisli category of (i.e. the category of cofree !-coalgebras) is cartesian monoidal. If is closed symmetric monoidal then the Kleisli category of a cartesian closed category, which is a categorical version of the translation of intuitionistic logic into linear logic.
Of course, the above definition depends on the existence of the cartesian product. A different definition that doesn’t require the existence of was given by Benton, Bierman, de Paiva, and Hyland:
Definition
Let be a symmetric monoidal category; a linear exponential comonad on is a lax monoidal comonad such that every cofree !-coalgebra naturally carries the structure of a comonoid object in the category of coalgebras (i.e. the cofree-coalgebra functor lifts to the category of comonoids in the category of coalgebras).
It follows automatically that all !-coalgebras are comonoids, and therefore that the category of all !-coalgebras (not just the cofree ones) is cartesian monoidal. Note that for a comonad on a poset, every coalgebra is free; thus the world of pure propositional “logic” doesn’t tell us whether to consider the Kleisli category or the Eilenberg-Moore category for the translation.
A more even-handed approach is the following (see Benton (1995) and Melliès (2009)), based on the observation that both Kleisli and Eilenberg-Moore categories are instances of adjunctions.
Definition
A linear-nonlinear adjunction is a monoidal adjunction in which is symmetric monoidal and is cartesian monoidal. The induced !-modality is the induced comonad on .
This includes both of the previous definitions where is taken respectively to be the Kleisli category or the Eilenberg-Moore category of !. Conversely, in any linear-nonlinear adjunction the induced comonad can be shown to be a linear exponential comonad. Moreover, if is a linear exponential comonad on a symmetric monoidal category with finite products, then the cofree !-coalgebra functor is a right adjoint and hence preserves cartesian products; but the cartesian products of coalgebras are the tensor products in , so we have , the Seely condition.
Classical case
For “classical” linear logic, we want to be not just (closed) symmetric monoidal but -autonomous. If an -autonomous category has a linear exponential comonad one can derive a ? from the ! by de Morgan duality, . The resulting relationship between ! and ? was axiomatized in a way not requiring the de Morgan duality by Blute, Cockett & Seely (1996):
Definition
Let be a linearly distributive category with tensor product and cotensor product . A (!,?)-modality on consists of:
-
a -monoidal comonad ! and a -comonoidal monad ?
-
? is a !-strong monad, and ! is a ?-strong comonad
-
all free !-coalgebras are naturally commutative -comonoids, and all free ?-algebras are naturally commutative -monoids.
Here a functor is strong with respect to a lax monoidal functor if there is a natural transformation of the form satisfying some natural axioms, and we similarly require compatibility of the monad and comonad structure transformations. BCS96 showed that if is in fact -autonomous, it follows from the above definition that , as expected.
Examples
Relation to Chu construction
Theorem
Suppose is a linear-nonlinear adjunction (Def. ), where is closed symmetric monoidal with finite limits and colimits, and is an object. Then there is an induced linear-nonlinear adjunction where is the Chu construction , which is -autonomous with finite limits and colimits. Hence admits a !-modality.
Proof
The embedding of in as is coreflective: the coreflection of is . Moreover, this subcategory is closed under the tensor product of , i.e. the embedding is strong monoidal, hence the adjunction is a monoidal adjunction. Therefore, the composite adjunction is again a linear-nonlinear-adjunction.
Note that this theorem is a direct consequence of the work of Yves Lafont and Thomas Streicher on game semantics using the Chu construction, together with Benton’s reformulation of linear logic in terms of monoidal adjunctions. Since a Chu construction is -autonomous, this !-modality implies a dual ?-modality.
Corollary
If is a cartesian closed category with finite limits and colimits and is an object, then there is a linear-nonlinear adjunction , and hence admits a !-modality.
Proof
Apply the previous theorem to the identity adjunction .
Note that the !-modality obtained from the corollary is idempotent, while that obtained from the theorem is idempotent if and only if the original one was. Other ways of constructing !-modalities, such as by cofree coalgebras, may produce examples that are not idempotent.
Realization in linear homotopy type theory
In dependent linear homotopy type theory the “linear-nonlinear adjunction” is naturally identified (Ponto & Shulman (2012), Ex. 4.2, see also Schreiber (2014), Sec. 4.2) with the stabilization adjunction between homotopy types and stable homotopy types (Riley (2022), Prop. 2.1.31), whose left adjoint (forming suspension spectra ) is equivalently given (cf. Riley (2022), Rem. 2.4.13) by sending to the linear dependent sum over the monoidal unit in the context . In terms of quantum modal logic this is forming the “linear randomization” of the given classical homotopy type (its “motive”):
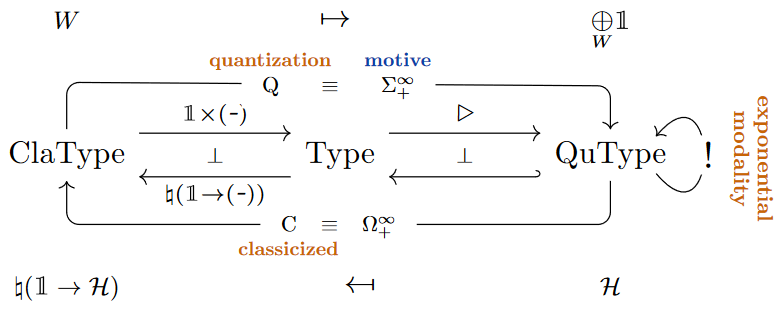
Curiously, this homotopy-theoretic realization of the exponential modality (beware the little subtlety of whether or not to reflect onto pointed homotopy types)
has independently been argued to have properties of an exponential map in the context of Goodwillie calculus, see there.
Moreover is a comonadic adjunction on simply connected homotopy types [Blomquist & Harper 2016 Thm. 1.8; Hess & Kedziorek 2017 Thm. 3.11], meaning that simply-connected classical (but pointed) homotopy types are identified with the -modales among stable homotopy types.
Antithesis interpretation
In the antithesis interpretation of affine logic into impredicative constructive mathematics, given the set of truth values , one can define a set of affine propositions by the set
The !-modality is a function is defined for each affine proposition by
Theorem
The !-modality is equal to the multiplicative conjunction of with itself
Proof
The multiplicative conjunction is given by
Given two propositions and such that , we have . Since intuitionistic conjunction is idempotent, we have
Modal term calculi
Girard’s original presentation of linear logic involved rules that explicitly assumed the presence of on hypotheses or on entire contexts, such as dereliction, weakening and contraction:
and “promotion”:
If this is translated into a natural deduction style term calculus, the resulting rules are more complicated than those of most type formers. This can be avoided using adjoint type theory with two context zones, one “nonlinear” one where contraction and weakening are permitted (and admissible) and one “linear” one where they are not, with as a modality relating the two zones.
Such a “modal” presentation of linear logic was first introduced by Girard 1993 and then developed by Plotkin 1993, Wadler 1993, Benton 1995, Barber 1996.
This presentation also generalizes naturally to dependent linear type theory, with the nonlinear type theory being dependent, and the linear types depending on the nonlinear ones but nothing depending on linear types. In this context, the -modality decomposes into “context extension” and a “dependent sum”.
Related concepts
References
General
The notion of the exponential modality originates in linear logic with
- Jean-Yves Girard, Linear logic, Theoretical Computer Science 50 1 (1987) [doi:10.1016/0304-3975(87)90045-4, pdf]
A streamlined statement of the inference rules and the observation that these make the exponential a comonad is due to:
-
R. A. G. Seely, §2 of: Linear logic, -autonomous categories and cofree coalgebras, in Categories in Computer Science and Logic, Contemporary Mathematics 92 (1989) [pdf, ps.gz, ISBN:978-0-8218-5100-5]
-
Valeria de Paiva, §2 of: The Dialectica Categories, in Categories in Computer Science and Logic, Contemporary Mathematics 92 (1989) [ISBN:978-0-8218-5100-5, doi:10.1090/conm/092]
Review:
- Anne Sjerp Troelstra, §12 in: Lectures on Linear Logic (1992) [ISBN:0937073776]
Brief survey in a context of computer science/linear type theory:
- Daniel Mihályi, Valerie Novitzká, Section 2.2 of: What about Linear Logic in Computer Science?, Acta Polytechnica Hungarica 10 4 (2013) 147-160 [pdf, pdf]
Further on the semantics of exponential conjunction as a comonad:
-
Valeria de Paiva, The Dialectica Categories, PhD thesis, technical report 213, Computer Laboratory, University of Cambridge (1991) [pdf, pdf]
-
Nick Benton, Gavin Bierman, Valeria de Paiva, §8 of: Term assignment for intuitionistic linear logic, Technical report 262, Computer Laboratory, University of Cambridge (August 1992) [pdf, pdf]
(published abridged as BBPH92)
-
Nick Benton, Gavin Bierman, Valeria de Paiva, Martin Hyland, Linear -Calculus and Categorical Models Revisited, in Computer Science Logic. CSL 1992, Lecture Notes in Computer Science 702, Springer (1993) [doi:10.1007/3-540-56992-8_6]
(abridged version of BBP92)
-
R. F. Blute , J. R. B. Cockett, R. A. G. Seely, ! and ? – Storage as tensorial strength, Mathematical Structures in Computer Science 6 4 (1996) 313-351 [doi:10.1017/S0960129500001055]
-
Martin Hyland and Andreas Schalk, Glueing and orthogonality for models of linear logic, pdf
and its resolution by a monoidal adjunction between the linear and a classical (intuitionistic) type system:
-
Gavin Bierman, On Intuitionistic Linear Logic, Cambridge (1994) [pdf, pdf]
-
Nick Benton, A mixed linear and non-linear logic: Proofs, terms and models, in Computer Science Logic. CSL 1994, Lecture Notes in Computer Science 933 (1995) 121-135 [doi:10.1007/BFb0022251, pdf]
Review:
-
Paul-André Melliès, Categorical models of linear logic revisited (2002) [hal:00154229]
-
Paul-André Melliès, Categorical semantics of linear logic, in Interactive models of computation and program behaviour, Panoramas et synthèses 27 (2009) 1-196 [web, pdf, pdf]
Construction of such comonads based on cofree comonoids:
-
Mellies and Tabareau and Tasson, An explicit formula for the free exponential modality of linear logic. Mathematical Structures in Computer Science, 28(7), 1253-1286. doi:10.1017/S0960129516000426
-
Sergey Slavnov, On Banach spaces of sequences and free linear logic exponential modality, Math. Struct. Comp. Sci. 29 (2019) 215-242, arXiv:1509.03853
The relation to Fock space is discussed in:
-
Richard Blute, Prakash Panangaden, R. A. G. Seely, Fock Space: A Model of Linear Exponential Types (1994) (web, pdf)
-
Marcelo Fiore, Differential Structure in Models of Multiplicative Biadditive Intuitionistic Linear Logic, Lecture Notes in Computer Science Volume 4583, 2007, pp 163-177 (pdf)
-
Jamie Vicary, A categorical framework for the quantum harmonic oscillator, International Journal of Theoretical Physics December 2008, Volume 47, Issue 12, pp 3408-3447 (arXiv:0706.0711)
(in the context of quantum information theory in terms of dagger-compact categories)
The interpretation of as an exponential in the context of Goodwillie calculus is due to
- Gregory Arone, Marja Kankaanrinta, The Goodwillie tower of the identity is a logarithm, 1995 (web)
based on
- Gregory Arone, Mark Mahowald, The Goodwillie tower of the identity functor and the unstable periodic homotopy of spheres, 1998 (pdf)
On the modal type theory-approach to a term calculus for the -modality:
-
Jean-Yves Girard. On the unity of logic Annals of Pure and Applied Logic 59 (1993) 201-217 [doi:10.1016/0168-0072(93)90093-S]
-
Gordon Plotkin, Type theory and recursion, in: Proceedings of the Eigth Symposium of Logic in Computer Science, Montreal , IEEE Computer Society Press (1993) 374 [doi:10.1109/LICS.1993.287571]
-
Philip Wadler, A syntax for linear logic, in: Ninth International Coference on the Mathematical Foundations of Programming Semantics, Lecture Notes in Computer Science 802 Springer (1993) [doi:10.1007/3-540-58027-1_24]
-
Andrew Barber, Dual Intuitionistic Linear Logic, Technical Report ECS-LFCS-96-347, University of Edinburgh (1996), [web, pdf, pdf]
A quantum programming language based on this linear/non-linear type theory adunction is QWIRE:
- Jennifer Paykin, Robert Rand, Steve Zdancewic, QWIRE: a core language for quantum circuits, POPL 2017: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming LanguagesJanuary 2017 Pages 846–858 (doi:10.1145/3009837.3009894)
theoretical background:
- Jennifer Paykin, Linear/non-Linear Types For Embedded Domain-Specific Languages, 2018 (upenn:2752)
applied to verified programming after implementation in Coq:
- Robert Rand, Jennifer Paykin, Steve Zdancewic, QWIRE Practice: Formal Verification of Quantum Circuits in Coq, EPTCS 266, 2018, pp. 119-132 (arXiv:1803.00699)
and using ambient homotopy type theory:
- Jennifer Paykin, Steve Zdancewic, A HoTT Quantum Equational Theory, talk at QPL2019 (arXiv:1904.04371)
The !-modality in affine logic applied to constructive mathematics:
- Michael Shulman, Affine logic for constructive mathematics. Bulletin of Symbolic Logic, Volume 28, Issue 3, September 2022. pp. 327 - 386 (doi:10.1017/bsl.2022.28, arXiv:1805.07518)
In dependent linear type theory
Discussion of the exponential modality via stabilization in dependent linear homotopy type theory:
-
Kate Ponto, Mike Shulman, Ex. 4.2 in: Duality and traces in indexed monoidal categories, Theory and Applications of Categories 26 23 (2012) [arXiv:1211.1555, tac:26-23, blog]
-
Urs Schreiber, Sec. 4.2 of: Quantization via Linear homotopy types [arXiv:1402.7041]
-
Mitchell Riley, §2.1.2 in: A Bunched Homotopy Type Theory for Synthetic Stable Homotopy Theory, PhD Thesis (2022) [doi:10.14418/wes01.3.139]
The comonadicity of simply connected pointed spaces over spectra:
-
Jacobson R. Blomquist, John E. Harper, Thm. 1.8 in: Suspension spectra and higher stabilization [arXiv:1612.08623]
-
Kathryn Hess, Magdalena Kedziorek, Thm. 3.11 in: The homotopy theory of coalgebras over simplicial comonads, Homology, Homotopy and Applications 21 1 (2019) [arXiv:1707.07104, doi:10.4310/HHA.2019.v21.n1.a11]
Last revised on January 14, 2025 at 15:42:19. See the history of this page for a list of all contributions to it.