Redirected from "advanced or retarded Green function".
Contents
Context
Differential geometry
Algebraic Quantum Field Theory
Contents
Idea
What are called advanced and retarded causal Green functions are Green functions for hyperbolic differential operators on manifolds with causal structure (e.g. spacetimes) whose support is in the future cone or past cone, respectively, of the source excitation. The corresponding integral kernels hence say how a point excitation propagates into the future or past, respectively, via the given differential equation, and therefore these are also called the advanced/future propagators.
If both advanced and retarded Green functions exist for a differential operator as well as for its formal adjoint, then the differental operator is called a Green hyperbolic differential operator. The archetypical examples are, on globally hyperbolic spacetimes:
-
normally hyperbolic differential operators such as the wave operator and the Klein-Gordon operator;
-
Dirac operators on spinor bundles whose square is a normally hyperbolic differential operator as above.
The advanced/retarded integral kernel
is such that
-
precisely if is in the causal future of ;
-
precisely if is in the causal past of .
Written as generalized functions these satisfy
This implies in particular that
- the causal propagator, which is the difference of the two
is skew-symmetric in its arguments (reflecting the fact that this is the integral kernel for the Peierls-Poisson bracket for the free scalar field on the given spacetime);
- the Dirac propagator, which is the sum of the two
is symmetric in its arguments, reflecting the fact that this is the integral kernel for time-ordered products away from the diagonal.
Definition
Definition
(compactly sourced causal support)
Given a vector bundle over a manifold with causal structure
Write for spaces of smooth sections, and write
for the linear subspaces on those smooth sections whose support is
-
() inside a compact subset
-
() inside the closed future cone/closed past cone, respectively, of a compact subset,
-
() inside the closed causal cone of a compact subset, which equivalently means that the intersection with every (spacelike) Cauchy surface is compact (Sanders 13, theorem 2.2),
-
() inside the past of a Cauchy surface (Sanders 13, def. 3.2),
-
() inside the future of a Cauchy surface (Sanders 13, def. 3.2),
-
() inside the future of one Cauchy surface and the past of another (Sanders 13, def. 3.2)
(Bär 14, section 1, Khavkine 14, def. 2.1)
Definition
(advanced and retarded Green functions, causal Green function and propagators)
Let be a smooth manifold with causal structure, let be a smooth vector bundle and let be a differential operator on its space of smooth sections.
Then a linear map
from spaces of sections of compact support to spaces of sections of causally sourced future/past support (def. ) is called an advanced or retarded Green function for , respectively, if
- for all we have
(1)
and
(2)
- the support of is in the closed future cone or closed past cone of the support of , respectively.
If the advanced/retarded Green functions exists, then the difference
is called the causal Green function.
If there are integral kernel, hence distributions in two variables
such that these Green functions are given by the corresponding integral transform, in that (in generalized function-notation)
then these integral kernels are called the advanced/retarded propagators; similarly then their difference
(3)
is the corresponding causal propagator.
(e.g. Bär 14, def. 3.2, cor. 3.10)
Properties
Existence and uniqueness
(Bär 14, cor. 3.12
Continuity
(Bär 14, 2.1, 2.2)
Definition
(distributional sections)
Let be a smooth vector bundle over a smooth manifold with causal structure.
The vector spaces of smooth sections with restricted support from def. structures of topological vector spaces via def. . We denote the topological dual spaces by
etc.
This is the space of distributional sections of the bundle .
With this notations, smooth compactly supported sections of the same bundle, regarded as the non-singular distributions, constitute a dense subset
Imposing the same restrictions to the supports of distributions as in def. , we have the following subspaces of distributional sections:
(Sanders 13, Bär 14)
Proposition
(causal Green functions of Green hyperbolic differential operators are continuous linear maps)
Given a Green hyperbolic differential operator (def. ), the advanced, retarded and causal Green functions of (def. ) are continuous linear maps with respect to the topological vector space structure from def. and also have a unique continuous extension to the spaces of sections with .larger support (def. ) as follows:
such that we still have the relation
and
and
(Bär 14, thm. 3.8, cor. 3.11)
Examples
For Klein-Gordon operator on Minkowski spacetime
On Minkowski spacetime consider the Klein-Gordon operator
Its Fourier transform is
The dispersion relation of this equation we write
(4)
where on the right we choose the non-negative square root.
We now discuss
-
Advanced and regarded propagators
-
Causal propagator
-
Wightman propagator
-
Feynman propagator
-
Singular support and Wave front sets
advanced and retarded propagators for Klein-Gordon equation on Minkowski spacetime
Proposition
(mode expansion of advanced and retarded propagators for Klein-Gordon operator on Minkowski spacetime)
The advanced and retarded Green functions of the Klein-Gordon operator on Minkowski spacetime are given by integral kernels (“propagators”)
by (in generalized function-notation)
where the advanced and retarded propagators have the following equivalent expressions:
Here denotes the dispersion relation (4) of the Klein-Gordon equation.
Proof
The Klein-Gordon operator is a Green hyperbolic differential operator (this example) therefore its advanced and retarded Green functions exist uniquely (prop. ). Moreover, prop. says that they are continuous linear functionals with respect to the topological vector space structures on spaces of smooth sections (def. ). In the case of the Klein-Gordon operator this just means that
are continuous linear functionals in the standard sense of distributions. Therefore the Schwartz kernel theorem implies the existence of integral kernels being distributions in two variables
such that, in the notation of generalized functions,
These integral kernels are the advanced/retarded “propagators”. We now compute these integral kernels by making an Ansatz and showing that it has the defining properties, which identifies them by the uniqueness statement of prop. .
We make use of the fact that the Klein-Gordon equation is invariant under the defnining action of the Poincaré group on Minkowski spacetime, which is a semidirect product group of the translation group and the Lorentz group.
Since the Klein-Gordon operator is invariant, in particular, under translations in it is clear that the propagators, as a distribution in two variables, depend only on the difference of its two arguments
(6)
Since moreover the Klein-Gordon operator is formally self-adjoint (this prop.) this implies that for the Klein the equation (2)
is equivalent to the equation (1)
Therefore it is sufficient to solve for the first of these two equation, subject to the defining support conditions. In terms of the propagator integral kernels this means that we have to solve the distributional equation
(7)
subject to the condition that the distributional support is
We make the Ansatz that we assume that , as a distribution in a single variable , is a tempered distribution
hence amenable to Fourier transform of distributions. If we do find a solution this way, it is guaranteed to be the unique solution by prop. .
By this prop. the distributional Fourier transform of equation (7) is
(8)
where in the second line we used the Fourier transform of the delta distribution from this example.
Notice that this implies that the Fourier transform of the causal propagator
satisfies the homogeneous equation:
(9)
Hence we are now reduced to finding solutions to (8) such that their Fourier inverse has the required support properties.
We discuss this by a variant of the Cauchy principal value:
Suppose the following limit of non-singular distributions in the variable exists in the space of distributions
meaning that for each bump function the limit in
exists. Then this limit is clearly a solution to the distributional equation (8) because on those bump functions which happen to be products with we clearly have
Moreover, if the limiting distribution (10) exists, then it is clearly a tempered distribution, hence we may apply Fourier inversion to obtain Green functions
To see that this is the correct answer, we need to check the defining support property.
Finally, by the Fourier inversion theorem, to show that the limit (10) indeed exists it is sufficient to show that the limit in (11) exists.
We compute as follows
(12)
where denotes the dispersion relation (4) of the Klein-Gordon equation. The last step is simply the application of Euler's formula .
Here the key step is the application of Cauchy's integral formula in the fourth step. We spell this out now for , the discussion for is the same, just with the appropriate signs reversed.
- If thn the expression decays with positive imaginary part of , so that we may expand the integration domain into the upper half plane as
Conversely, if then we may analogously expand into the lower half plane.
- This integration domain may then further be completed to two contour integrations. For the expansion into the upper half plane these encircle counter-clockwise the poles at , while for expansion into the lower half plane no poles are being encircled.
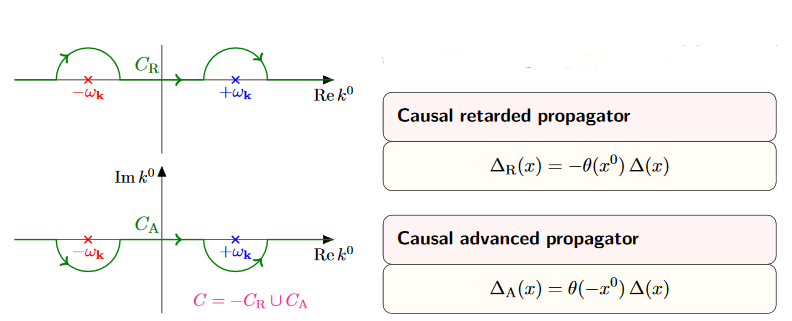
-
Apply Cauchy's integral formula to find in the case the sum of the residues at these two poles times , zero in the other case. (For the retarded propagator we get times the residues, because now the contours encircling non-trivial poles go clockwise).
-
The result is now non-singular at and therefore the limit is now computed by evaluating at .
This computation shows a) that the limiting distribution indeed exists, and b) that the support of is in the future, and that of is in the past.
Hence it only remains to see now that the support of is inside the causal cone. But this follows from the previous argument, by using that the Klein-Gordon equation is invariant under Lorentz transformations: This implies that the support is in fact in the future of every spacelike slice through the origin in , hence in the closed future cone of the origin.
Corollary
(causal propagator is skew-symmetric)
Under reversal of arguments the advanced and retarded causal propagators from prop. are related by
It follows that the causal propagator is skew-symmetric in its arguments:
Proof
By prop. we have with (5)
Here in the second step we applied change of integration variables (which introduces no sign because in addition to the integration domain reverses orientation).
causal propagator
Proposition
(mode expansion of causal propagator for Klein-Gordon equation on Minkowski spacetime)
The causal propagator (3) for the Klein-Gordon equation for mass on Minkowski spacetime is given, in generalized function notation, by
(13)
where in the second line we used Euler's formula .
In particular this shows that the causal propagator is real, in that it is equal to its complex conjugate
(14)
Proof
By definition and using the expression from prop. for the advanced and retarded causal propagators we have
For the reality, notice from the last line that
where in the last step we used the change of integration variables (whih introduces no sign, since on top of the orientation of the integration domain changes).
We consider a couple of equivalent expressions for the causal propagator which are useful for computations:
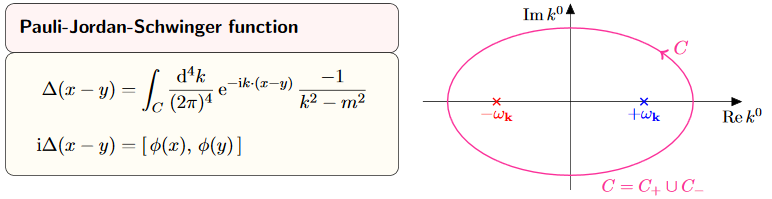
graphics grabbed from Kocic 16
Proof
By Cauchy's integral formula we compute as follows:
The last line is the expression for the causal propagator from prop.
Proof
By decomposing the integral over into its negative and its positive half, and applying the change of integration variables we get
The last line is the expression for the causal propagator from prop. .
Wightman propagator
Prop. exhibits the causal propagator of the Klein-Gordon operator on Minkowski spacetime as the difference of a contribution for positive temporal angular frequency (hence positive energy and a contribution of negative temporal angular frequency.
The positive frequency contribution to the causal propagator is called the Wightman propagator (def. below), also known as the the vacuum state 2-point function of the free real scalar field on Minkowski spacetime. Notice that the temporal component of the wave vector is proportional to the negative angular frequency
(see at plane wave), therefore the appearance of the step function in (15) below:
Definition
(Wightman propagator or vacuum state 2-point function for Klein-Gordon operator on Minkowski spacetime)
The Wightman propagator for the Klein-Gordon operator at mass on Minkowski spacetime is the tempered distribution in two variables which as a generalized function is given by the expression
(15)
Here in the first line we have in the integrand the delta distribution of the Fourier transform of the Klein-Gordon operator times a plane wave and times the step function of the temporal component of the wave vector. In the second line we used the change of integration variables , then the definition of the delta distribution and the fact that is by definition the non-negative solution to the Klein-Gordon dispersion relation.
(e.g. Khavkine-Moretti 14, equation (38) and section 3.4)
Proposition
(contour integral representation of the Wightman propagator for the Klein-Gordon operator on Minkowski spacetime)
The Wightman propagator from def. is equivalently given by the contour integral
(16)
where the Jordan curve runs counter-clockwise, enclosing the point , but not enclosing the point .
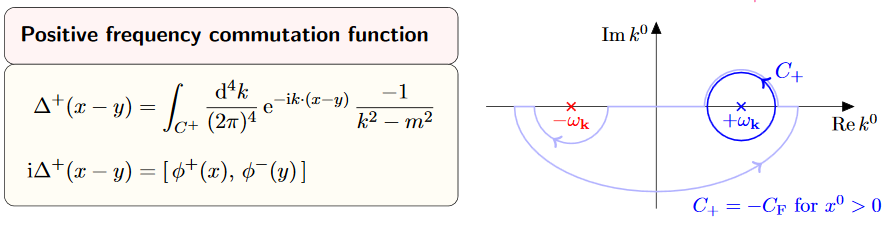
graphics grabbed from Kocic 16
Proof
We compute as follows:
The last step is application of Cauchy's integral formula, which says that the contour integral picks up the residue of the pole of the integrand at . The last line is , by definition .
Proposition
(skew-symmetric part of Wightman propagator is the causal propagator)
The Wightman propagator for the Klein-Gordon equation on Minkowski spacetime (def. ) is of the form
(17)
where
-
is the causal propagator (prop. ), which is real (14) and skew-symmetric (prop. )
-
is real and symmetric
Proof
By applying Euler's formula to (15) we obtain
(18)
On the left this identifies the causal propagator by (13), prop. .
The second summand changes, both under complex conjugation as well as under , via change of integration variables (because the cosine is an even function). This does not change the integral, and hence is symmetric.
Feynman propagator
We have seen that the positive frequency component of the causal propagator for the Klein-Gordon equation on Minkowski spacetime (prop. ) is the Wightman propagator (def. ) given, according to prop. , by (17)
There is an evident variant of this combination, which will be of interest:
Proposition
(mode expansion for Feynman propagator of Klein-Gordon equation on Minkowski spacetime)
The Feynman propagator (def. ) for the Klein-Gordon equation on Minkowski spacetime is given by the following equivalent expressions
Similarly the anti-Feynman propagator is equivalently given by
Proof
By the mode expansion of from (5) and the mode expansion of from (18) we have
where in the second line we used Euler's formula. The last line follows by comparison with (15) and using that the integral over is invariant under .
The computation for is the same, only now with a minus sign in front of the cosine:
As before for the causal propagator, there are equivalent reformulations of the Feynman propagator, which are useful for computations:
Proof
We compute as follows:
Here
-
In the first step we introduced the complex square root . For this to be compatible with the choice of non-negative square root for in (4) we need to choose that complex square root whose complex phase is one half that of (instead of that plus π). This means that is in the upper half plane and is in the lower half plane.
-
In the third step we observe that
-
for the integrand decays for positive imaginary part and hence the integration over may be deformed to a contour which encircles the pole in the upper half plane;
-
for the integrand decays for negative imaginary part and hence the integration over may be deformed to a contour which encircles the pole in the lower half plane
and then apply Cauchy's integral formula which picks out times the residue a these poles.
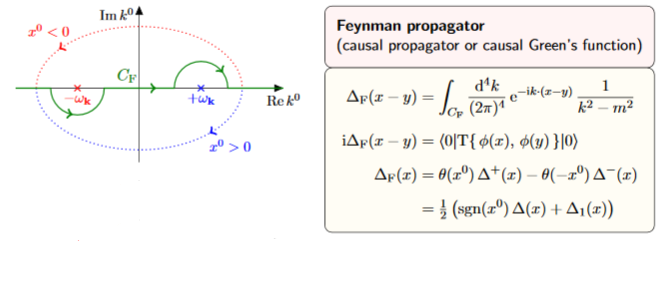
Notice that when completing to a contour in the lower half plane we pick up a minus signs from the fact that now the contour runs clockwise.
-
In the fourth step we used prop. .
singular support and wave front sets
We now discuss the singular support and the wave front sets of the various propagators for the Klein-Gordon equation on Minkowski spacetime.
Proof
By prop. the causal propagator is equivalently the Fourier transform of distributions of the delta distribution of the mass shell times the sign function of the angular frequency; and by basic properties of the Fourier transform this is the convolution of distributions of the separate Fourier transforms:
By (Gel’fand-Shilov 66, III 2.11 (7), p 294), see this prop., the singular support of the first convolution factor is the light cone.
The second factor is
(by this example and this example) and hence the wave front set of the second factor is
(by this example and this example).
With this the statement follows, via a partition of unity, from this prop..
For illustration we now make this general argument more explicit in the special case of spacetime dimension
by computing an explicit form for the causal propagator in terms of the delta distribution, the Heaviside distribution and smooth Bessel functions.
We follow (Scharf 95 (2.3.18)).
Consider the formula for the causal propagator in terms of the mode expansion (13). Since the integrand here depends on the wave vector only via its norm and the angle it makes with the given spacetime vector via
we may express the integration in terms of polar coordinates as follws:
In the special case of spacetime dimension this becomes
(19)
Here in the second but last step we renamed and doubled the integration domain for convenience, and in the last step we used the trigonometric identity .
In order to further evaluate this, we parameterize the remaining components of the wave vector by the dual rapidity , via
as
which makes use of the fact that is non-negative, by construction. This change of integration variables makes the integrals under the braces above become
(20)
Next we similarly parameterize the vector by its rapidity . That parameterization depends on whether is spacelike or not, and if not, whether it is future or past directed.
First, if is spacelike in that then we may parameterize as
which yields
where in the last line we observe that the integrand is a skew-symmetric function of .
Second, if is timelike with then we may parameterize as
which yields
(21)
Here in the last line we identified the integral representation of the Bessel function of order 0 (see here). The important point here is that this is a smooth function.
Similarly, if is timelike with then the same argument yields
In conclusion, the general form of is
Therefore we end up with
(22)
Proof
By prop. the causal propagator is equivalently the Fourier transform of distributions of the delta distribution of the mass shell times the sign function of the angular frequency; and by basic properties of the Fourier transform this is the convolution of distributions of the separate Fourier transforms:
By (Gel’fand-Shilov 66, III 2.11 (7), p 294), see this prop., the singular support of the first convolution factor is the light cone.
The second factor is
(by this example and this example) and hence the wave front set of the second factor is
(by this example and this example).
With this the statement follows, via a partition of unity, from this prop..
For illustration, we now make this general statement fully explicit in the special case of spacetime dimension
by computing an explicit form for the causal propagator in terms of the delta distribution, the Heaviside distribution and smooth Bessel functions.
We follow (Scharf 95 (2.3.36)).
By (18) we have
The first summand, proportional to the causal propagator, which we computed as (22) in prop. to be
The second term is computed in a directly analogous fashion: The integrals from (20) are now
Parameterizing by rapidity, as in the proof of prop. , one finds that for timelike this is
while for spacelike it is
where we identified the integral representations of the Neumann function (see here) and of the modified Bessel function (see here).
As for the Bessel function in (21) the key point is that these are smooth functions. Hence we conclude that
This expression has singularities on the light cone due to the step functions. In fact the expression being differentiated is continuous at the light cone (Scharf 95 (2.3.34)), so that the singularity on the light cone is not a delta distribution singularity from the derivative of the step functions. Accordingly it does not cancel the singularity of as above, and hence the singular support of is still the whole light cone.
(e.g DeWitt 03 (27.85))
Proof
By prop. the Feynman propagator is equivalently the Cauchy principal value of the inverse of the Fourier transformed Klein-Gordon operator:
With this the statement follows immediately from the result (Gel’fand-Shilov 66, III 2.8 (8) and (9), p 289), see this prop..
Proposition
(wave front sets of propagators of Klein-Gordon equation on Minkowski spacetime)
The wave front set of the various propagators for the Klein-Gordon equation on Minkowski spacetime, regarded, via translation invariance, as distributions in a single variable, are as follows:
- the causal propagator (prop. ) has wave front set all pairs with and both on the lightcone:
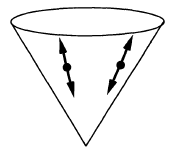
-
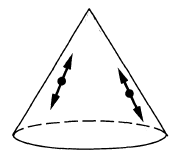
- the Wightman propagator (def. ) has wave front set all pairs with and both on the light cone and :
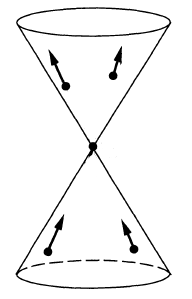
- the Feynman propagator (def. ) has wave front set all pairs with and both on the light cone and
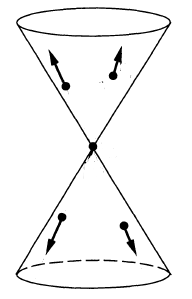
(Radzikowski 96, (16))
Proof
First regarding the causal propagator:
By prop. the singular support of is the light cone.
Since the causal propagator is a solution to the homogeneous Klein-Gordon equation, the propagation of singularities theorem says that also all wave vectors in the wave front set are lightlike. Hence it just remains to show that all non-vanishing lightlike wave vectors based on the lightcone in spacetime indeed do appear in the wave front set.
To that end, let be a bump function whose compact support includes the origin.
For a point on the light cone, we need to determine the decay property of the Fourier transform of . This is the convolution of distributions of with . By prop. we have
This means that the convolution product is the smearing of the mass shell by .
Since the mass shell asymptotes to the light cone, and since for on the light cone (given that is on the light cone), this implies the claim.
Now for the Wightman propagator:
By def. its Fourier transform is of the form
Moreover, its singular support is also the light cone (prop. ).
Therefore now same argument as before says that the wave front set consists of wave vectors on the light cone, but now due to the step function factor it must satisfy .
Finally regarding the Feynman propagator:
By prop. the Feynman propagator coincides with the positive frequency Wightman propagator for and with the “negative frequency Hadamard operator” for . Therefore the form of now follows directly with that of above.
For Dirac operator on Minkowski spacetime
Finally we observe that the propagators for the Dirac field on Minkowski spacetime follow immediately from the propagators for the scalar field:
Proposition
(advanced and retarded propagator for Dirac equation on Minkowski spacetime)
Consider the Dirac operator on Minkowski spacetime, which in Feynman slash notation reads
Its advanced and retarded propagators (def. ) are the derivatives of distributions of the advanced and retarded propagators for the Klein-Gordon equation (prop. ) by :
Hence the same is true for the causal propagator:
Proof
Applying a differential operator does not change the support of a smooth function, hence also not the support of a distribution. Therefore the uniqueness of the advanced and retarded propagators (prop. ) together with the translation-invariance and the anti-formally self-adjointness of the Dirac operator (as for the Klein-Gordon operator (6) implies that it is sufficent to check that applying the Dirac operator to the yields the delta distribution. This follows since the Dirac operator squares to the Klein-Gordon operator:
Similarly we obtain the other propagators for the Dirac field from those of the real scalar field:
Definition
(Wightman propagator for Dirac operator on Minkowski spacetime)
The Wightman propagator for the Dirac operator on Minkowski spacetime is the positive frequency part of the causal propagator (prop. ), hence the derivative of distributions of the Wightman propagator for the Klein-Gordon field (def. ) by the Dirac operator:
Here we used the expression (?) for the Wightman propagator of the Klein-Gordon equation.
Definition
(Feynman propagator for Dirac operator on Minkowski spacetime)
The Feynman propagator for the Dirac operator on Minkowski spacetime is the linear combination
of the Wightman propagator (def. ) and the retarded propagator (prop. ). By prop. this means that it is the derivative of distributions of the Feynman propagator of the Klein-Gordon equation (def. ) by the Dirac operator
propagators (i.e. integral kernels of Green functions)
for the wave operator and Klein-Gordon operator
on a globally hyperbolic spacetime such as Minkowski spacetime:
| name | symbol | wave front set | as vacuum exp. value
of field operators | as a product of
field operators |
|---|
| causal propagator | | 
 | | Peierls-Poisson bracket |
| advanced propagator | |  | | future part of
Peierls-Poisson bracket |
| retarded propagator | |  | | past part of
Peierls-Poisson bracket |
| Wightman propagator | |  | | positive frequency of
Peierls-Poisson bracket,
Wick algebra-product,
2-point function
of vacuum state
or generally of
Hadamard state |
| Feynman propagator | |  | | time-ordered product |
(see also Kocic‘s overview: pdf)
References
General discussion includes
-
Christian Bär, Green-hyperbolic operators on globally hyperbolic spacetimes, Communications in Mathematical Physics 333, 1585-1615 (2014) (doi, arXiv:1310.0738)
-
Igor Khavkine, Covariant phase space, constraints, gauge and the Peierls formula, Int. J. Mod. Phys. A, 29, 1430009 (2014) (arXiv:1402.1282)
based on
Textbook discussion for free fields in Minkowski spacetime is in
An overview of the Green functions of the Klein-Gordon operator, hence of the Feynman propagator, advanced propagator, retarded propagator, causal propagator etc. is given in
- Mikica Kocic, Invariant Commutation and Propagation Functions Invariant Commutation and Propagation Functions, 2016 (pdf)
Discussion on general globally hyperbolic spacetimes includes
-
F. Friedlander, The Wave Equation on a Curved Space-Time, Cambridge: Cambridge University Press, 1975
-
Christian Bär, Nicolas Ginoux, Frank Pfäffle, Wave Equations on Lorentzian Manifolds and Quantization, ESI Lectures in Mathematics and Physics, European Mathematical Society Publishing House, ISBN 978-3-03719-037-1, March 2007, Softcover (arXiv:0806.1036)
-
Nicolas Ginoux, Linear wave equations, Ch. 3 in Christian Bär, Klaus Fredenhagen, Quantum Field Theory on Curved Spacetimes: Concepts and Methods, Lecture Notes in Physics, Vol. 786, Springer, 2009
Review in the context of perturbative algebraic quantum field theory includes
- Katarzyna Rejzner, sections 4.1 and 6.2.3 of Perturbative Algebraic Quantum Field Theory, Mathematical Physics Studies, Springer 2016 (pdf)







