nLab nonabelian cohomology
Context
Cohomology
Special and general types
-
group cohomology, nonabelian group cohomology, Lie group cohomology
-
-
cohomology with constant coefficients / with a local system of coefficients
Special notions
Variants
-
differential cohomology
Extra structure
Operations
Theorems
Contents
- Idea
- More details
- Ordinary Principal Bundles
- Ordinary Nonabelian Cohomology
- Ordinary Abelian Cohomology
- Ordinary Characteristic Classes
- Ordinary Character Map
- Ordinary Connections
- More history
- Properties
- Special cases
- Examples
- Objects classified by nonabelian cohomology
- Related concepts
- References
Idea
The notion of cohomology finds its natural general formulation in terms of hom-spaces in an (∞,1)-topos, as described at cohomology. Many of the cohomologies which have been traditionally considered, such as sheaf cohomology, turn out to be just a special case of the general situation, for objects which are sufficiently abelian in the sense of stable (∞,1)-categories.
Therefore to amplify that one is looking at general cohomology without restricting to abelian cohomology one speaks of nonabelian cohomology.
To say this in a bit more detail (following SS24):
Cohomology via classifying spaces
It is a classical and yet possibly undervalued fact that reasonable cohomology theories have classifying spaces (and more generally classifying stacks). To quickly recall (more details and pointers in FSS23, §2):
Ordinary cohomology. This begins with the observation that (reduced) ordinary singular cohomology, with coefficients in a discrete abelian group , is classified in degree by Eilenberg-MacLane spaces – in that on well-behaved topological spaces , notably on smooth manifolds, there are natural isomorphisms between the ordinary cohomology groups and the connected components of the respective (pointed) mapping spaces:
This equivalence makes manifest the characteristic properties of cohomology: homotopy invariance, exactness and wedge property, since these are now immediately implied by general abstract properties of mapping spaces.
Moreover, these EM-spaces are in fact loop spaces of each other, via weak homotopy equivalences
that thereby represent the suspension isomorphisms between ordinary cohomology groups, as follows:
Ordinary non-abelian cohomology. Note here that it is the loop space property (2), and hence the corresponding suspension isomorphism, which reflect the fact that the coefficient has been assumed to be an abelian group: For a non-abelian group , an Eilenberg-MacLane space still exists (cf. classifying space), but is not a loop space.
While the suspension isomorphism is thus lost for non-abelian coefficients, the assignment
still satisfies homotopy invariance, exactness and wedge property, just as before by the general properties of mapping spaces, and hence has all the characteristic properties of ordinary cohomology – except for its abelian-ness. Accordingly, (3) is known as non-abelian cohomology, famous from early applications in Chern-Weil theory.
Whitehead-generalized cohomology. If or as long as we do insist on abelian cohomology groups related by suspension isomorphisms, we may still immediately generalize ordinary cohomology in the form (1), simply by using any other sequence of classifying spaces , being successive loop spaces of each other as in (2),
as such called a sequential -spectrum of spaces, or just a spectrum, for short. The Brown representability theorem says that the resulting assignments
are equivalently the “generalized cohomology theories” as introduced by Whitehead, including examples such as K-theory, elliptic cohomology and cobordism cohomology.
Non-abelian generalized cohomology. But as we just saw, suspension isomorphisms are to be regarded as extra structure on cohomology. Not necessarily requiring them leads to consider any pointed space (which we may as well assume to be connected) as the classifying space of a non-abelian generalized cohomology theory, defined in evident generalization of (3) simply by
Here the notation on the left is suggestive of the fact that any loop space canonically carries the structure of a higher homotopy-coherent group – a groupal -space or -group, for short – whose de-looping is equivalent to the connected component of the original space:
For example, in the archetypical case where is the -sphere, then the non-abelian generalized cohomology theory that it classifies is known as (unstable) Cohomotopy
in dual reference to the familar homotopy groups
Another example of non-abelian generalized cohomology is unstable topological K-theory, whose classifying spaces are taken to be finite stages of the sequential colimits which construct the classifying spaces of topological K-theory.
Developing non-abelian cohomology
Fundamental, elementary and compelling as the notion of non-abelian generalized cohomology in (4) is, it has long remained underappreciated. For example, none of the original authors on Cohomotopy (6) address their subject as a cohomology theory, instead the early development revolves around partial fixes for the perceived defect of co-homotopy sets to not in general carry group structure. The situation does not improve with the early development of “non-abelian gerbes”, whose original description appears unwieldy.
Explicit acknowledgement of (stacky) non-abelian generalized cohomology in the transparent guise (4) appears only in a lecture of Toën 2002, (possibly following Simpson 2002 where non-abelian generalization of de Rham cohomology is considered).
Two independent developments around 2009 put non-abelian generalized cohomology into practical context:
-
The discovery of nonabelian Poincaré duality (Lurie 2009 §3.8), relating non-abelian cohomology (as later made explicit in Lurie 2014 Def. 6) of manifolds to “non-abelian homology” in the guise of “topological chiral homology” (which, in contrast to non-abelian cohomology, takes work to define);
-
The observation in theoretical physics (SS 2008, Sc 2009) that charge/flux-quantization laws for higher gauge fields are generally in non-abelian cohomology.
With non-abelian generalized cohomology thus recognized as a worthwhile subject, one is led to generalize familiar constructions in abelian cohomology, as far as possible, and to explore the consequences.
First, one may straightforwardly equip non-abelian cohomology with further attributes: Considering the right hand side of (4) not just for plain spaces but for sheaves of spaces (higher stacks) leads to non-abelian generalized sheaf cohomology, including, in particular, non-abelian generalized versions of twisted cohomology, of equivariant cohomology and nonabelian differential cohomology.
Equivariant non-abelian cohomology. Via the above identification of cohomology sets with homotopy-classes of maps to a classifying space, every flavor of homotopy theory comes with its corresponding flavor of cohomology theories.
In equivariant homotopy theory one considers topological spaces equipped with the action of a (finite, for our purposes) group and with -equivariant maps between them – and the corresponding flavor of cohomology is equivariant cohomology:
Here the notion of -homotopy equivalence of maps is straightforward but, at face value, technically cumbersome to reason about. However, Elmendorf's theorem reveals that -homotopy equivalences (between -cell complexes) are nothing but systems of ordinary weak homotopy equivalences between the -fixed spaces for all subgroups . These systems of fixed spaces are conveniently re-packaged as presheaves on a small category called the orbit category of , whence -equivariant homotopy theory is equivalently the homotopy theory of presheaves of spaces on .
Twisted non-abelian cohomology. Somewhat similarly, given any space in any homotopy theory, the -slice is the homotopy theory whose objects are spaces fibered over with maps between them respecting the fibration up to specified homotopy. If we assume, without essential restriction, that the base space is connected, then we may identify it as , as in (5), which exhibits any fibration over it as the Borel construction of the homotopy-quotient of a homotopy-coherent action .
If we now think of a domain object in this -slice as a twist and of a codomain object as a local coefficient bundle, then the corresponding non-abelian cohomology is just the homotopy classes of sections of the -associated -fiber bundle, and as such is -twisted -cohomology:
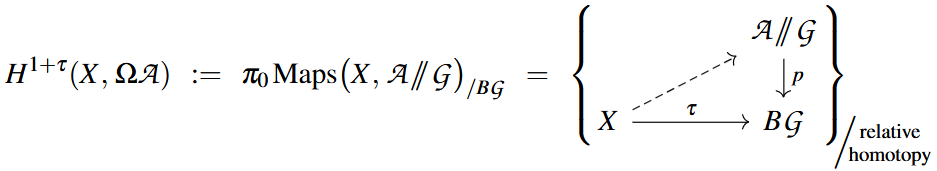
This works generally: If all spaces here are in addition equipped with -actions as in (7), hence if we are looking at a slice of equivariant homotopy, then the above is automatically twisted equivariant non-abelian cohomology.
The non-abelian character. One famous construction on abelian cohomology is the Chern-Dold character map to de Rham cohomology, which in the case of K-cohomology becomes the familar Chern character (and which on ordinary cohomology is essentially just the de Rham theorem). One may think of the Chern-Dold character as universally extracting the non-torsion data of cohomology. Its generalization to non-abelian cohomology was developed in FSS23:
Observing that the Chern-Dold character is essentially just the cohomology operation induced by rationalization of the classifying space,
as such it makes sense in the generality of non-abelian classifying spaces (immediately so under mild technical assumptions, such as nilpotency, but with more work also more generally). In view of this, the fundamental theorem of dg-algebraic rational homotopy theory may be re-cast as a non-abelian de Rham theorem which identifies, over smooth manifolds , the resulting non-abelian rational cohomology with the concordance classes of flat differential forms having coefficients in the real Whitehead-bracket -algebra of the classifying space:

Since generalized cohomology theories are typically hard to analyze, in particular non-abelian ones, this character map may be regarded as extracting the first non-trivial stage of more tractable invariants. For instance, the character of a non-abelian class is the first obstruction to the trivialization of that class.
Nonabelian cohomology and gauge fields. In the mentioned application to physics, the flux densities of a higher gauge field are sourced by charges which appear as classes in non-abelian de Rham cohomology on the right, and the completion of the higher gauge theory by a flux-quantization law means to lift these charges through the character map to classes in a chosen non-abelian cohomology theory on the left.
Cohomology and gauge fields. While cohomology has of course many and diverse applications, in physics no less than in other fields, the role of cohomology specifically in the global description of (higher) gauge fields (“force fields”) is profound: In generalization of the seminal historical observation (“Dirac charge quantization”) that electromagnetic field configurations are globally to be identified with 2-cocycles in ordinary differential cohomology of spacetime, higher gauge field species are similarly to be identified with generalized cohomology theories whose further properties and attributes closely reflect the field’s physical nature, as indicated in the above table.
More details
Ordinary Principal Bundles
For a Hausdorff-topological group, a principal -bundle over a base space is a map such that there exists an open cover over which is identified with the trivial fibration in a way that the fibers are identified by -valued transition functions on double overlaps of charts, :
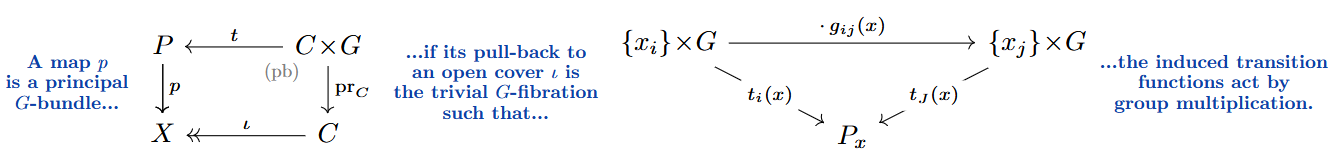
These transition functions clearly satisfy on triple overlaps the Čech cocycle condition
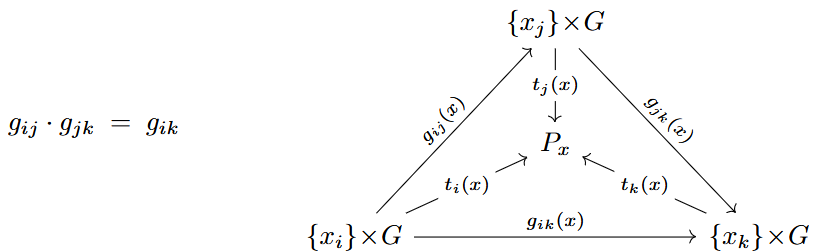
and transform under a principal bundle isomorphism by the Čech coboundary relation
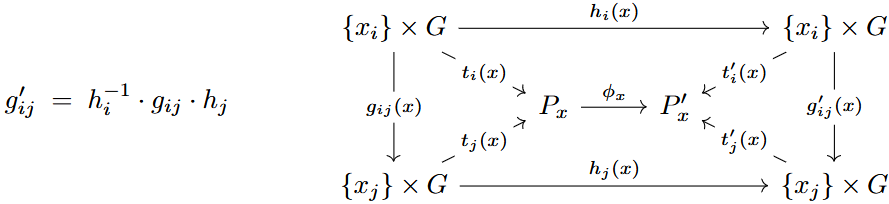
whence the isomorphism classes of principal bundles map to the Čech cohomology of the base space:
As indicated, this map is in fact a bijection (for well-behaved , such as smooth manifolds), as one finds effectively by reading the above construction in reverse.
The outer parts of these diagrams then also show that if we write
-
for the topological groupoid with a single object and worth of morphisms,
-
for the topological groupoid with as its manifold of objects and as its manifold of morphisms,
for a *good* open cover (over which every -bundle trivializes),
then the groupoid of principal -bundles is identified with the groupoid of continuous functors with continuous natural transformations between these:

Ordinary Nonabelian Cohomology
A deeper but classical theorem says (cf. SS25 Thm. 4.1.3) that this situation is preserved by the “topological realization” of topological groupoids to topological spaces
under which a continuous functor becomes a continuous map from to the classifying space – which still represents isomorphism classes of principal -bundles:
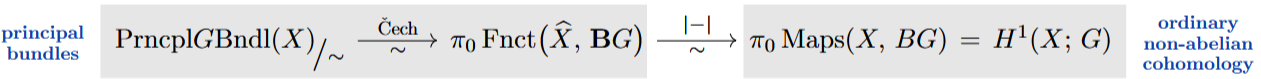
This is the ordinary nonabelian cohomology of .
Ordinary Abelian Cohomology
In the special case that an abelian group, one readily sees that there is a fiber-wise -tensor product of principal -bundles
given by
which makes the isomorphism classes naturally form an abelian group.
(NB: As a tensor product of fibrations this exists also for non-abelian , but the commutativity of is needed for its principality, namely for the resulting transition functions to again by given by group multiplication.)
Under the classification of principal -bundles by -cohomology, this means that the classifying space (may be chosen such that it) carries topological group structure itself!, so that the construction iterates:
For a discrete abelian group (such as ) these higher-order classifying spaces are also denoted “” and called “Eilenberg-MacLane spaces”:
But this means that for abelian group coefficients there is higher-degree -cohomology appearing as a special case of non-abelian cohomology, as follows:
Of course, when is discrete then there is also Čech cohomology and singular cohomology with coefficients in . A classical theorem says that (on our smooth manifold domain ) all these notions of ordinary cohomology agree, hence that
Ordinary Characteristic Classes
Thereby we obtain an immediate means to approximate non-abelian cohomology by abelian cohomology: Every map of classifying spaces , hence every universal characteristic class
induces a cohomology operation from non-abelian to abelian cohomology, simply by composition of classifying maps:
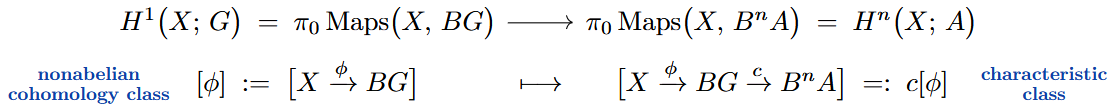
For example, the frame bundle of a Riemannian manifold is an -principal bundle, whose classifying space carries universal Pontrjagin classes , which evaluate to the Pontrjagin classes of :
We see again that:
Ordinary Character Map
One more notion of cohomology available on smooth manifolds is de Rham cohomology , which we may understand – non-traditionally but equivalently FSS23 Prop. 6.4 – as equivalence classes of closed differential forms modulo concordance of closed forms:
By the de Rham isomorphism, this, too, coincides with a special case of our general notion of cohomology, namely with abelian cohomology for coefficients the real numbers (regarded as a discrete topological group).
Combined with the cohomology operation induced by extension of scalars , hence by the induced , this gives a map from integral to de Rham cohomology, which we may call the ordinary character map
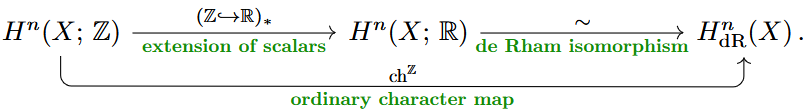
Beware that this character map is not in general injective, in fact it forgets exactly the torsion subgroups of the integral cohomology group. Nevertheless — or rather: therefore! — the ordinary character map provides the first approximation to integral cohomology, which is generally more readily computed than the full integral cohomology.
In consequence, when applied to integral characteristic classes then the ordinary character gives a useful first approximation to ordinary non-abelian cohomology. Specifically for unitary principal bundles we obtain a sequence of Chern-de Rham classes:

But since de Rham cohomology is a local differential-geometric notion, the question arises:
Connections are the answer to this question.
Ordinary Connections
For a Lie group and its Lie algebra, we denote the (functor assigning) flat -valued differential forms by
There is a universal such flat form, called the Maurer-Cartan form , in that the flat forms on any Cartesian space , , are the pullbacks of the MC-form along smooth maps , unique up to rigid translation along the group:
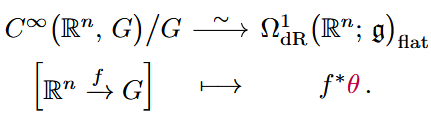
Hence on a trivial -bundle we have a flat form which restricts on each fiber to the MC-form.
On a non-trivial principal -bundle we still find a -valued differential form that restricts on each fiber to the MC-form, but it may not itself be flat anymore, the failure being its curvature
which is therefore a measure for the non-triviality of , at least if we also demand that it is a horizontal form in that it vanishes on vectors tangent to the fibers – in this case is called a principal connection.
Cartan calculus then shows that all -invariant polynomials evaluated on the curvature 2-form are in fact closed basic forms in that they are pulled back from closed forms on the base manifold:

Thus: Connections on principal bundles extract de Rham classes on their base space measuring their non-triviality.
That these indeed give the above Chern-de Rham classes is the content of the Chern-Weil theorem.
More history
It was originally apparently John Roberts who understood (remarkably: while thinking about quantum field theory in the guise of AQFT) that general cohomology is about coloring simplices in -categories.
- John E. Roberts, Mathematical Aspects of Local Cohomology, in: Algèbres d’opérateurs et leurs applications en physique mathématique, Colloques Internationaux du Centre National de la Recherche Scientifique (C.N.R.S) 274, Paris (1979) 321–332 [ISBN:2-222-02441-2, pdf, pdf]
This is recounted in
- Ross Street, pages 9-10 of: An Australian conspectus of higher category theory, talk at Institute for Mathematics and its Applications Summer Program: -Categories: Foundations and Applications at the University of Minnesota (Minneapolis, 7–18 June 2004), in: Towards Higher Categories, The IMA Volumes in Mathematics and its Applications 152, Springer (2010) 237-264 [pdf, pdf, doi:10.1007/978-1-4419-1524-5]
Parallel to this development of the notion of descent and codescent there was the development of homotopical cohomology theory as described in
- Kenneth S. Brown, Abstract Homotopy Theory and Generalized Sheaf Cohomology, Transactions of the American Mathematical Society, Vol. 186 (1973), 419-458 (pdf)
The two approaches are different, but closely related. Their relation is via the notion of codescent.
There is a chain of inclusions
along which one can generalize the coefficient objects of ordinary cohomology. (See strict omega-groupoid, strict omega-category). Since doing so in particular generalizes abelian groups to nonabelian groups (but goes much further!) this is generally addressed as leading to nonabelian cohomology.
Depending on the models chosen, there are different concrete realizations of nonabelian cohomology.
For instance nonabelian Čech cohomology played a special role in the motivation of the notion of gerbes (see in particular gerbe (in nonabelian cohomology)), concretely thought of in terms of pseudofunctors at least in the context of nonabelian group cohomology, while more abstract (and less explicit) homotopy theory methods dominate the discussion of infinity-stacks.
Either way, one obtains a notion of cohomology on -categories with coefficients in -catgories. This is, most generally, the setup of “nonabelian cohomology”.
This is conceptually best understood today in terms of higher topos theory, using (infinity,1)-categories of (infinity,1)-sheaves.
This perspective on nonabelian cohomology is discussed for instance in Toen 02
Properties
Postnikov decomposition and Whitehead principle
In an (∞,1)-topos every object has a Postnikov tower in an (∞,1)-category. This means that in some sense general nonabelian cohomology can be decomposed into nonabelian cohomology in degree 1 and abelian cohomology in higher degrees, twisted by this nonabelian cohomology. This has been called (Toën) the Whitehead principle of nonabelian cohomology.
Special cases
Nonabelian group cohomology
Sometimes the term nonabelian cohomology is used in a more restrictive sense. Often people mean nonabelian group cohomology when they say nonabelian cohomology, hence restricting to the domains to groups, which are groupoids with a single object.
This kind of nonabelian cohomology is discussed for instance in
That and how ordinary group cohomology is reproduced from the homotopical cohomology theory of strict omega-groupoids is discussed in detail in chapter 12 of
- Ronnie Brown, P. Higgins, R. Sivera, Nonabelian algebraic topology.
For more see
Nonabelian sheaf cohomology with constant coefficients
For a topological space and an ∞-groupoid, the standard way to define the nonabelian cohomology of with coefficients in is to define it as the intrinsic cohomology as seen in ∞Grpd Top:
where is the geometric realization of and the fundamental ∞-groupoid of .
But both and here naturally can be regarded, in several ways, as objects of (∞,1)-sheaf (∞,1)-toposes over nontrivial (∞,1)-sites . The intrinsic cohomology of such is a nonabelian sheaf cohomology. The following discusses two such choices for such that the corresponding nonabelian sheaf cohomology coincides with (for paracompact ).
Petit -sheaf -topos
For a topological space and its category of open subsets equipped with the canonical structure of an (∞,1)-site, let
be the (∞,1)-category of (∞,1)-sheaves on . The space itself is naturally identified with the terminal object . This is the petit topos incarnation of .
Write
be the global sections terminal geometric morphism.
Under the constant (∞,1)-sheaf functor an an ∞-groupoid is regarded as an object .
There is therefore the intrinsic cohomology of the -topos with coefficients in the constant (∞,1)-sheaf on
This is cohomology with constant coefficients.
Notice that since is in fact the terminal object of and that is in fact that global sections functor, this is equivalently
Theorem
If is a paracompact space, then these two definitins of nonabelian cohomology of with constant coefficients agree:
This is HTT, theorem 7.1.0.1. See also (∞,1)-category of (∞,1)-sheaves for more.
Gros -sheaf -topos
Another alternative is to regard the space as an object in the cohesive (∞,1)-topos ETop∞Grpd.
with the further left adjoint to being the intrinsic fundamental ∞-groupoid in a locally ∞-connected (∞,1)-topos functor. The intrinsic nonabelian cohomology in there also coincides with nonabelian cohomology in Top; even the full cocycle ∞-groupoids are equivalent:
Theorem
For paracompact we have an equivalence of cocycle ∞-groupoids
and hence in particular an isomorphism on cohomology
Proof
See ETop∞Grpd.
Examples
Examples of generalized nonabelian cohomology (with general classifying spaces):
Objects classified by nonabelian cohomology
For a cocycle in nonabelian cohomology, we say the homotopy fibers of is the object classified by .
For examples and discussion of this see
Related concepts
References
Classical theory – bundles and groups
The classical notion of non-abelian (Čech-)cohomology in degree 1 and its relation to fiber bundles/principal bundles:
-
Alexander Grothendieck, Chapter V of: A General Theory of Fibre Spaces With Structure Sheaf, University of Kansas, Report No. 4 (1955, 1958) [pdf, pdf]
-
Jean Frenkel, Cohomologie à valeurs dans un faisceau non abélien, C. R. Acad. Se., t. 240 (1955) 2368-2370
-
Jean Frenkel, Cohomologie non abélienne et espaces fibrés, Bulletin de la Société Mathématique de France, 85 (1957) 135-220 [numdam:BSMF_1957__85__135_0]
Review:
- Torsten Wedhorn, Torsors and Non-abelian Čech Cohomology, chapter 7 in: Manifolds, Sheaves, and Cohomology, Springer (2016) [doi:10.1007/978-3-658-10633-1]
Review in topological spaces (via classifying spaces):
-
Nicolas Addington, Fiber bundles and nonabelian cohomology, talk at Graduate Student Topology Conference (2007) [pdf]
-
Stephen Mitchell, around Theorem 7.4 in: Notes on principal bundles and classifying spaces, Lecture Notes. University of Washington (2011) [pdf, pdf]
-
Gerd Rudolph, Matthias Schmidt, Thm. 3.5.1 of: Differential Geometry and Mathematical Physics Part II. Fibre Bundles, Topology and Gauge Fields, Springer (2017) [doi:10.1007/978-94-024-0959-8]
See also:
- Jinpeng An. Zhengdong Wang, Nonabelian cohomology with coefficients in Lie groups, Trans. Amer. Math. Soc. 360 (2008) 3019-3040 [doi:10.1090/S0002-9947-08-04278-5]
The case of nonabelian group cohomology:
- James Milne, Section 27.a (of the pdf, not present in the published version) of: Algebraic Groups, Cambridge University Press 2017 (doi:10.1017/9781316711736, webpage, pdf)
Categorified theory – 2-bundles/gerbes
Early discussion, of higher non-abelian cohomology with coefficients in certain 2-groups (implicitly):
-
Paul Dedecker, Cohomologie à coefficients non abéliens et espaces fibrés, Bulletins de l’Académie Royale de Belgique 41 (1955) 1132-1146 [persee:barb_0001-4141_1955_num_41_1_69497]
-
Paul Dedecker, Cohomologie de dimension 2 à coefficients non abéliens, C. R. Acad. Sci. Paris 247 (1958) 1160-1163 [BnF]
-
Paul Dedecker, Sur La Cohomologie Non Abelienne I (Dimension Deux), Canadian Journal of Mathematics 12 (1960) 231-251 [doi:10.4153/CJM-1960-019-7]
and with coefficients in certain 3-groups presented by crossed squares:
-
Paul Dedecker, A. Frei, Les relations d’équivalence des morphismes de la suite exacte de cohomologie non abêlienne, C. R. Acad. Sci. Paris 262 (1966) 1298-1301
-
Paul Dedecker, Three dimensional non-abelian cohomology for groups, Category theory, homology theory and their applications, II (Battelle Institute Conf.) 1969 (MathSciNet)
The correct definition using crossed modules of sheaves then appeared in
- Raymond Debremaeker, Cohomologie met waarden in een gekruiste groepenschoof op een situs, PhD thesis, 1976 (Katholieke Universiteit te Leuven). English translation: Cohomology with values in a sheaf of crossed groups over a site, arXiv:1702.02128
Of algebraic structures:
- René Lavendhomme, J. R. Roisin, Cohomologie non abélienne de structures algèbriques, Journal of Algebra 67 2 (1980) 385-414 [doi:10.1016/0021-8693(80)90168-4]
Discussion in terms of gerbes:
-
Jean Giraud, Cohomologie non abélienne , Springer (1971) [doi:10.1007/978-3-662-62103-5]
(aspects of classification of -gerbes by cohomology with coefficients in the automorphism 2-group , but imposes extra constraints)
-
Larry Breen, Bitorseurs et cohomologie non-Abélienne, The Grothendieck Festschrift: a collection of articles written in honour of the 60th birthday of Alexander Grothendieck, Vol. I, edited P.Cartier, et al., Birkhäuser, Boston, Basel, Berlin, 401-476, (1990) (doi:10.1007/978-0-8176-4574-8_10)
-
John Duskin: Non-abelian cohomology in a topos, reprinted as: Reprints in Theory and Applications of Categories 23 (2013) 1-165 [tac:tr23]
-
Ieke Moerdijk: Lie Groupoids, Gerbes, and Non-Abelian Cohomology, K-Theory 28 3 (2003) 207-258 [journal, doi:10.1023/A:1026251115381]
-
Amnon Yekutieli, Combinatorial descent data for gerbes, Journal of Noncommutative Geometry 8 4 (2014) 1083–1099 [arXiv:1109.1919, webpage]
-
Alexander Campbell, A higher categorical approach to Giraud’s non-abelian cohomology, PhD thesis, Macquarie University (2016) [hdl:1959.14/1261186]
Existence of classifying spaces for principal 2-bundles/nonabelian gerbes:
- John Baez, Danny Stevenson, The Classifying Space of a Topological 2-Group, In: Baas N., Friedlander E., Jahren B., Østvær P. (eds.) Algebraic Topology, Abel Symposia, vol 4. Springer 2009 (arXiv:0801.3843, doi:10.1007/978-3-642-01200-6_1)
General theory – -bundles/-gerbes
Discussion of the general theory via principal ∞-bundles and/or ∞-gerbes and/or ∞-stacks:
- Paul Glenn, Realization of cohomology classes in arbitrary exact categories, J. Pure Appl. Algebra 25, 1982, no. 1, 33- 105 (doi:10.1016/0022-4049(82)90094-9)
In a context of nonabelian Hodge theory:
-
Carlos Simpson, The Hodge filtration on nonabelian cohomology, in: János Kollár, Robert Lazarsfeld, David Morrison (eds.) Algebraic Geometry Santa Cruz 1995, Part 2, Proceedings of Symposia in Pure Mathematics Volume 62.2, AMS 1997 (arXiv:alg-geom/9604005, doi:10.1090/pspum/062.2)
-
Carlos Simpson, Secondary Kodaira-Spencer classes and nonabelian Dolbeault cohomology (arXiv:alg-geom/9712020)
-
Carlos Simpson: Algebraic aspects of higher nonabelian Hodge theory, in: Fedor Bogomolov, Ludmil Katzarkov (eds.), Motives, polylogarithms and Hodge theory, Part II (Irvine, CA, 1998), Int. Press Lect. Ser., 3, II, Int. Press, (2002, 2016) 417-604 [arXiv:math/9902067, ISBN:9781571462909]
-
Carlos Simpson, Tony Pantev, Ludmil Katzarkov, Nonabelian mixed Hodge structures (arXiv:math/0006213)
Generally:
-
Bertrand Toën, Def. 6.0.6 in: Stacks and Non-abelian cohomology, lecture at Introductory Workshop on Algebraic Stacks, Intersection Theory, and Non-Abelian Hodge Theory, MSRI (2002) [slides, ps, pdf, pdf]
-
J. F. Jardine, Z. Luo, Higher principal bundles, Mathematical Proceedings of the Cambridge Philosophical Society, Volume 140, Issue 2 March 2006 , pp. 221-243 (pdf, doi:10.1017/S0305004105008911)
-
J. F. Jardine, Cocycle categories, In: Nils Baas, Eric Friedlander, B. Jahren , Arne Østvær (eds.) Algebraic Topology, Abel Symposia, vol 4. Springer 2009 (arXiv:math/0605198, doi:10.1007/978-3-642-01200-6_8)
-
Jacob Lurie, Thm. 7.1.0.1 in: Higher Topos Theory, Annals of Mathematics Studies 170, Princeton University Press 2009 (pup:8957, pdf)
-
Matthias Wendt, Classifying spaces and fibrations of simplicial sheaves, Journal of Homotopy and Related Structures 6 1 (2011) 1-38 [arXiv:1009.2930, JHRS:6-1]
-
David Roberts, Danny Stevenson, Simplicial principal bundles in parametrized spaces, New York Journal of Mathematics Volume 22 (2016) 405-440 (arXiv:1203.2460, nyjm:22-19)
-
Danny Stevenson, Classifying theory for simplicial parametrized groups (arXiv:1203.2461)
-
Thomas Nikolaus, Urs Schreiber, Danny Stevenson, Principal ∞-bundles – General theory, Journal of Homotopy and Related Structures 10 4 (2015) 749-801 [doi:10.1007/s40062-014-0083-6, arXiv:1207.0248]
-
Thomas Nikolaus, Urs Schreiber, Danny Stevenson, Principal ∞-bundles – Presentations, Journal of Homotopy and Related Structures 10 3 (2015) 565-622 [doi:10.1007/s40062-014-0077-4, arXiv:1207.0249]
-
John F. Jardine: Non-abelian Cohomology, chapter 9 in: Local Homotopy Theory, Springer Monographs in Mathematics (2015) [doi:10.1007/978-1-4939-2300-7_9]
On cohomology operations on components of Whitehead-generalized cohomology theories seen in non-abelian cohomology:
- John Michael Boardman, David Copeland Johnson, W. Stephen Wilson, Unstable Operations in Generalized Cohomology (pdf), in: Ioan Mackenzie James (ed.) Handbook of Algebraic Topology Oxford 1995 (doi:10.1016/B978-0-444-81779-2.X5000-7)
The suggestion that every (pointed) space/-stack may be regarded as being the classifying space of a non-abelian cohomology theory, and that this is what defines non-abelian cohomology in general:
-
Hisham Sati, Urs Schreiber et al., p 41 of: Twisted differential nonabelian cohomology (2008) [pdf, pdf]
-
Urs Schreiber: Background fields in twisted differential nonabelian cohomology, talk at Oberwolfach Workshop, June 2009 – Strings, Fields, Topology, Oberwolfach Report 28 (2009) 1578-1582 [pdf, doi:10.4171/owr/2009/28]
(in twisted and differential generality)
-
Jacob Lurie, Def. 6 in: Nonabelian Poincaré Duality, Lecture 8 in Tamagawa Numbers via Nonabelian Poincaré Duality (282y) (2014) [pdf, pdf]
(in view of nonabelian Poincaré duality)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, The Character Map in Nonabelian Cohomology — Twisted, Differential, Generalized, World Scientific (2023) [arXiv:2009.11909, doi:10.1142/13422]
(generalizing the Chern-Dold character to nonabelian cohomology in this sense)
Unstable classification of topological phases
Arguments that some effects in topological phases of matter are “unstable” or “fragile” in that the relevant deformation class of their valence bundles over the Brillouin torus is not their class in topological K-theory (as assumed by the K-theory classification of topological phases of matter) but an unstable homotopy class (what may be called a class in generalized nonabelian cohomology) such as of maps to a Grassmannian space (or more general flag variety) classifying (systems of) sub-bundles of a trivial vector bundle of fixed finite rank:
Influential precursor discussion:
- Andreas P. Schnyder, Shinsei Ryu, Akira Furusaki, Andreas W. W. Ludwig: Classification of topological insulators and superconductors in three spatial dimensions, Phys. Rev. B 78 195125 (2008) [doi:10.1103/PhysRevB.78.195125, arXiv:0803.2786]
More explicit highlighting of the role of the unstable case (and coinage of the term “fragile” for “unstable”):
-
Hoi Chun Po, Haruki Watanabe, Ashvin Vishwanath: Fragile Topology and Wannier Obstructions, Phys. Rev. Lett. 121 (2018) 126402 [doi:10.1103/PhysRevLett.121.126402]
-
Hoi Chun Po, Liujun Zou, T. Senthil, Ashvin Vishwanath: Faithful tight-binding models and fragile topology of magic-angle bilayer graphene, Phys. Rev. B 99 (2019) 195455 [doi:10.1103/PhysRevB.99.195455, arXiv:1808.02482]
-
Adrien Bouhon, Tomáš Bzdušek, Robert-Jan Slager: Geometric approach to fragile topology beyond symmetry indicators, Phys. Rev. B 102 (2020) 115135 [doi:10.1103/PhysRevB.102.115135, arXiv:2005.02044]
Applications:
-
Adrien Bouhon, Robert-Jan Slager, around equation (3) in: Multi-gap topological conversion of Euler class via band-node braiding: minimal models, PT-linked nodal rings, and chiral heirs [arXiv:2203.16741]
-
Zory Davoyan, Wojciech J. Jankowski, Adrien Bouhon, Robert-Jan Slager, section II.A in: Three-dimensional -symmetric topological phases with Pontryagin index [doi:10.1103/PhysRevB.109.165125 arXiv:2308.15555]
Expositions with an eye towards non-abelian braiding of band nodes in momentum space:
-
Gunnar F. Lange: Multi-gap topology & non-abelian braiding in -space, talk at University of Oslo (Feb 2023) pdf]
-
Adrien Bouhon: Non-Abelian and Euler multi-gap topologies in crystalline materials, talk at: Quantum Information and Quantum Matter, CQTS @ NYU Abu Dhabi (May 2023) pdf]
Further discussion:
-
Barry Bradlyn, Zhijun Wang, Jennifer Cano, B. Andrei Bernevig: Disconnected Elementary Band Representations, Fragile Topology, and Wilson Loops as Topological Indices: An Example on the Triangular Lattice, Phys. Rev. B 99 (2019) 045140 [doi:10.1103/PhysRevB.99.045140, arXiv:1807.09729]
-
Zhi-Da Song, Luis Elcoro, B. Andrei Bernevig: Real Space Invariants: Twisted Bulk-Boundary Correspondence of Fragile Topology, Science 367 6479 (2020) 794-797 [doi:10.1126/science.aaz7650, arXiv:1910.06869]
-
Zhida Song, L. Elcoro, Nicolas Regnault, B. Andrei Bernevig: Fragile Phases As Affine Monoids: Classification and Material Examples, Phys. Rev. X 10 031001 (2020) [doi:10.1103/PhysRevX.10.031001, arXiv:1905.03262]
-
Simon Becker, Zhongkai Tao, Mengxuan Yang: Fragile topology on solid grounds: a mathematical perspective [arXiv:2502.03442]
Last revised on June 12, 2025 at 08:58:16. See the history of this page for a list of all contributions to it.