nLab function extensionality
Context
Set theory
- fundamentals of set theory
- material set theory
- presentations of set theory
- structuralism in set theory
- class-set theory
- constructive set theory
- algebraic set theory
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Discrete and concrete objects
typical contexts
Contents
- Idea
- Definition
- In set theory
- In category theory
- In dependent type theory
- Judgmental function extensionality
- For judgmental equality of sections
- Properties
- Relation to weak function extensionality
- Relation to the univalence axiom
- Relation to interval types
- Relation to equality reflection
- Relation to propositional logic
- Categorical semantics
- See also
- References
Idea
The principle of functional extensionality states that two functions are equal if their values are equal at every argument.
Definition
In set theory
In set theory, in the same way that the axiom of choice has internal and external versions, depending on whether one uses the external logic? or the internal logic of the set theory, function extensionality also has internal and external versions.
External function extensionality
In set theory, let denote the unique singleton up to bijection. There are multiple notions of external function extensionality, due to the different possible notions of function and element in set theory:
-
for all sets and and functions and , if and only if for all elements , .
-
for all sets and and functions and , if and only if for all functions , .
-
for all sets and and elements of the function set and , if and only if for all elements , .
-
for all sets and and elements of the function set and , if and only if for all elements of the function set , .
The first is the one most commonly found in foundations of categorical set theories with separate notions of element and function. The second is the one most commonly found in foundations of categorical set theories where an element is defined as a function out of the terminal set .
The first and the third notions of function extensionality are equivalent to each other, since for every set theory with function sets, the category of sets is a cartesian closed category, which means that there is a bijection between the hom-sets
and thus for every function there is a unique element of a function set , and for every element of a function set there is a unique function .
Internal function extensionality
In set theory, let denote the unique singleton up to bijection and let denote the Cartesian product of a family of sets . For all sets , let denote the diagonal function; this means that the preimage of at , , is a subsingleton, and is a family of sets.
The principle of internal function extensionality is given by one of the two equivalent statements:
-
given sets and , one can derive the element of the set
-
given sets and , one can derive the element of the set
This is the set theoretic analogue of the axiom of function extensionality found in dependent type theories, where functions are elements of function types, the type theoretic analogue of function sets, and equalities are represented by identity types, the type theoretic analogue of the diagonal one-to-one correspondence, and is true in any set theory with Cartesian products of arbitrary families of sets as well as function sets.
In category theory
Generalizing external function extensionality
There are multiple ways to extend the set-theoretic definition of external function extensionality from the category of sets to more general categories.
-
The first notion of external function extensionality extends from the category of sets to any concrete category , where objects are specific kinds of sets (such as groups, rings, topological spaces, et cetera) and morphisms are specific kinds of functions between sets (such as group homomorphisms, ring homomorphisms, continuous maps, et cetera).
-
The second notion of external function extensionality extends from the category of sets to any well-pointed category , and corresponds to the statement that the terminal object is an extremal generator in category, and is one of the conditions for making a pretopos a well-pointed pretopos. This definition is satisfied in any concrete category . This is not the same as the first notion of external function extensionality, since not every concrete category is well-pointed, and not every well-pointed category is concrete: Grp is concrete but not well-pointed, while an arbitrary model of ETCS is well-pointed but not necessarily concrete.
-
The third and fourth notions of external function extensionality extends from the category of sets to any concrete cartesian closed category , and is equivalent to the first notion in any concrete cartesian closed category.
None of these notions are called “function extensionality” in category theory. The term “function extensionality” is reserved for the generalization of internal function extensionality to arbitrary categories, as documented in the next section.
Generalizing internal function extensionality
The notion of function extensionality in a category arises from the generalization of the set-theoretic definition of internal function extensionality from the category of sets to more general categories. In particular, similar to internal function extensionality, it is the logical formulation of function extensionality in the internal language of the category. The “internal” formulation can be interpreted in a category with a rich enough internal language. For instance, function extensionality can be stated in the Mitchell-Benabou language and is true in any topos. So every topos internally satisfies function extensionality despite the fact that toposes do not generally satisfy the external notion of being concrete or well-pointed. This is because the quantifier in the internal language is interpreted as a quantification over all generalized elements rather than merely the global elements . Then the statement when quantifying over generalized elements is true as a consequence of the definition of an exponential object.
In dependent type theory
In intensional type theory, the notion of equality is replaced by identifications, these being terms of identity type . Since such identity type are in general not mere propositions, care needs to be exercised in stating function extensionality in intensional type theory:
For types and parallel functions , there are the following two canonical functions (from identity types of function types to dependent products of pointwise identity types), which one may use for expressing function extensionality (2), both defined via path induction (see function application to identifications) as shown now:
(These two definitions of become the same under singleton contractibility. The second definition behaves better with the function application to identifications.)
In general, both functions are not equivalences of types in intensional type theory: two functions could be defined in different ways, and thus be intensionally different, yet produce the same values on all inputs (i.e. be extensionally the same).
Function extensionality is then the statement that the function (1) is an equivalence of types after all, for all functions :
(e.g. UFP13 (2.9.1)).
In the generality of dependent functions (using the notation here) this reads:

(In this dependent generality this is a special case of UFP13, Lem. 2.9.7.)
Compare this to the analogous extensionality principle for dependent pairs (see there):
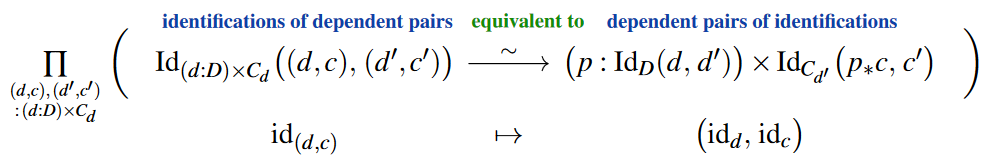
Judgmental function extensionality
One could replace the equivalences of types above with judgmental equality of types, which results in judgmental function extensionality. Applied to each definition, judgmental function extensionality states that for all all types and and functions and
and
respectively.
For judgmental equality of sections
Suppose that given functions and , for all , and are judgmentally equal to each other . Then it follows that and are judgmentally equal to each other, , and thus function extensionality holds. This result is crucial in the proof of function extensionality from an interval type with judgmental computation rules.
Properties
There are a number of axioms in dependent type theory which imply function extensionality. These include
- weak function extensionality
- univalence axiom
- an interval type with judgmental computation rules
- equality reflection in extensional type theory
- the axiom which states that every type is a mere proposition.
Relation to weak function extensionality
Function extensionality is equivalent to weak function extensionality – see at References – General.
Relation to the univalence axiom
In homotopy type theory, the univalence axiom implies type-theoretic function extensionality (2) – see at References – in HoTT.
Relation to interval types
Postulating an interval type with judgmental computation rules for the point constructors of the interval type implies function extensionality.
The proof assumes a typal uniqueness rule for function types. Let be the function application to identities, be concatenation of identities (i.e. transitivity), and be the inverse of identities (i.e. symmetry).
First the proof constructs a function from a dependent function , inductively defined by
Then it uses the properties of function types, product types, currying, uncurrying, and the symmetry of products , to construct a function , inductively defined by
If the interval type has judgmental computation rules for the point constructors, then and for all , which implies that and for all , and subsequently that and . This means that there are identities and , and an identity
thus proving function extensionality.
An interval type with only typal computation rules for the point constructors does not imply function extensionality. This is because the proof with the judgmental computation rules uses the fact that and for all implies that and . However, if the computation rules are typal, then the equivalent statement is that having identities and for all implies that there are identities and , which is precisely function extensionality, and so cannot be used to prove function extensionality.
Relation to equality reflection
To do: write how extensional type theory automatically satisfies function extensionality.
…
Relation to propositional logic
To do: write how requiring all types to be mere propositions in dependent type theory, such as in propositional logic as a dependent type theory automatically satisfies function extensionality.
…
Categorical semantics
Under the standard relation between type theory and category theory, the categorical semantics of the type of pointwise identifications between a pair of parallel functions is the space of sections over (hence the right base change along) of the pullback
where
-
now denote objects in any given ambient categorical model of dependent types which serve as the categorical semantics for the types of the same name,
-
denotes any “very good” path space object (see there) of .
Since the right base change is right adjoint to pullback, this means that the categorical semantics of global elements of , whose immediate categorical semantics is as maps out of the terminal object (to be denoted “”):
is equivalently given by maps of the form
These in turn (now by the defining universal property of the pullback) are equivalent to maps of the form
hence to lifts of through the path fibration display map.
In contrast, the categorical semantics of the global type of identifications is by maps of the form
where
-
denotes the internal hom in the ambient categorical model of dependent types —
if one assumes a cartesian closure, then this is equivalently denoted as an exponential objects: .
So the categorical semantics of function extensionality (2) says in particular that there is a map
which serves to lift global elements as above.
Of course we are not just interested in global elements here. What we really want is an actual section of in the slice over (although this can be derived from the global element formulation by using the Yoneda lemma together with currying and uncurrying tricks), such that this exhibits a weak equivalence.
Proposition
Function extensionality holds in the internal type theory of a type-theoretic fibration category precisely if dependent products (i.e. right base change) along fibrations preserve acyclic fibrations.
Example
The condition in prop. holds in particular in right proper Cisinski model structures, since in these right base change along fibrations is a right Quillen functor (see e.g. the proof here).
Notice that every presentable locally Cartesian closed (∞,1)-category (by the discussion there) has a presentation by a right proper Cisinski model category. Accordingly we may say that every presentable locally Cartesian closed (∞,1)-category interprets HoTT+FunExt.
See also
References
General
Discussion of variants of function extensionality in Martin-Löf type theory, and their relation:
-
Richard Garner, On the strength of dependent products in the type theory of Martin-Löf, Annals of Pure and Applied Logic 160 1 (2009) 1-12 [arXiv:0803.4466, doi:10.1016/j.apal.2008.12.003]
-
Peter LeFanu Lumsdaine, Strong functional extensionality from weak (2011) [blog post]
Proofs of function extensionality from an interval type with judgmental computation rules:
- Mike Shulman, An interval type implies functional extensionality (2011) [blog post]
In homotopy type theory
Discussion of function extensionality in homotopy type theory and proof that it is implied by univalence:
Original announcement in:
- Vladimir Voevodsky, p. 8 of: Univalent Foundations Project (2010) [pdf, pdf]
Textbook accounts:
-
Univalent Foundations Project, §2.9 & §4.9 Homotopy Type Theory – Univalent Foundations of Mathematics (2013) [web, pdf]
-
Egbert Rijke, §13 in: Introduction to Homotopy Type Theory, Cambridge Studies in Advanced Mathematics, Cambridge University Press [arXiv:2212.11082]
Exposition:
- Carlo Angiuli, Univalence implies function extensionality (2011) [blog post, pdf]
Tutorial for formalization in Coq:
Formalization in cubical Agda:
Discussion of the categorical semantics in the context of homotopy type theory:
- Michael Shulman, Univalence for inverse diagrams and homotopy canonicity, Mathematical Structures in Computer Science, Volume 25, Issue 5 ( From type theory and homotopy theory to Univalent Foundations of Mathematics ) June 2015 (arXiv:1203.3253, doi:/10.1017/S0960129514000565)
On definitional function extensionality in higher observational type theory:
- Mike Shulman, Towards Third-Generation HOTT – Part 1 (2022) [slides, video]
Last revised on March 11, 2024 at 18:17:42. See the history of this page for a list of all contributions to it.