nLab flavour (particle physics)
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
The fermion fundamental particles in the standard model of particle physics arrange in three “generations”. Between generations, particles differ in their mass and in further properties referred to as flavor quantum numbers, but otherwise their interactions are the same, to high accuracy. Hence flavor physics refers to the phenomenology of processes that do involve or depend on flavor quantum numbers, notably when flavor changes through interactions via the weak nuclear force and Yukawa interactions.
For the leptons these flavor quantum numbers are electron number, muon number and tauon number as well as the corresponding three neutrino numbers.
For the quarks the flavor quantum numbers are isospin, charm, strange-ness, bottom-ness and top-ness.
See yotams for a good quick introduction.
Properties
The flavor problem
In the standard model of particle physics, the sector involving flavor physics – hence the Higgs boson interaction with the generations of fermions, hence the Yukawa coupling- and CKM matrix-sector in the Lagrangian density of the Einstein-Yang-Mills-Dirac-Higgs theory that defines the standard model – has some striking characteristics different from the sector that does not:

slide grabbed from Altmannshofer 14
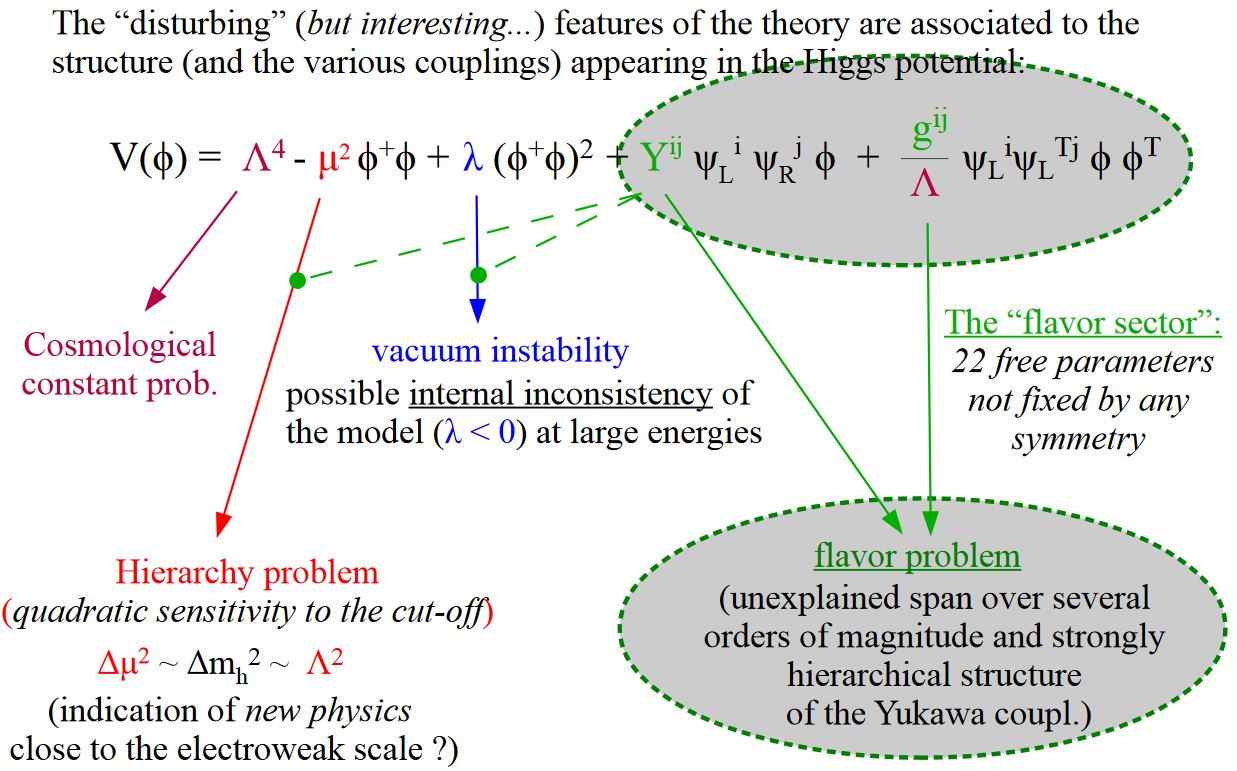
slide grabbed from Isidori 16
(Note that Isidori’s slide collects all terms with a Higgs boson factor, including the pure Higgs terms reflecting the cosmological constant and the hierarchy problem, and hence “all the problematic terms”, while the flavor sector proper consists of those terms involving Higgs and quark factors.)
Broadly, the flavor problem (see the references below) is the fact that the nature and principles behind the flavor sector of the standard model are much less understood than those of the gauge sector (the “color sector”). More concretely, the flavor problem in models going beyond the standard model (such as GUT models and/or the MSSM) is that introducing any New Physics while satisfying observational constraints on flavor physics seems to demand a high level of fine-tuning in the flavor sector.
Moreover, all observed CP violation is related to flavor-changing interactions.
Finally, due to confinement, the flavor-changing transitions between quarks are not seen in isolation by collider experiments, but are only seen via the induced decays of the mesons and/or baryons that the quarks are bound in. This way the flavor problem is tied to the confinement problem and hence to the problem of formulating QCD non-perturbatively (e.g. via AdS/QCD).
All this suggests that the flavor sector is controlled by mechanisms that are not understood or identified yet.
Experimental “anomalies”
Due to the flavor problem, the flavor sector of the standard model of particle physics is the least well understood in detail. Indeed, thete are persistent and growing discrepancies between SM-predictions and experimental measurements in the flavor sector:
Flavor anomaly
flavor anomalies reflect a discrepancy in B-meson decays between experiment (LHCb, Belle, BaBar) and theoretical computations, which keeps being seen at a global statistical significance of across all experiments and decay channels. If these flavour anomalies are real they signify New Physics in the flavor sector.
See at flavour anomalies for more.
Cabibbo anomaly
See at Cabibbo anomaly and V_cb puzzle.
anomaly
See at (g-2) anomaly.
Geometric engineering on D8-branes
In geometric engineering of flavor physics in intersecting D-brane models, the flavour degrees of freedom come from open strings ending on spacetime-filling D-branes called “flavor branes” (Karch-Katz 02).
Specifically in the Sakai-Sugimoto model geometrically engineering something close to actual quantum chromodynamics (Sakai-Sugimoto 04, Sakai-Sugimoto 05), flavour is encoded in the presence of D8-branes in the model:
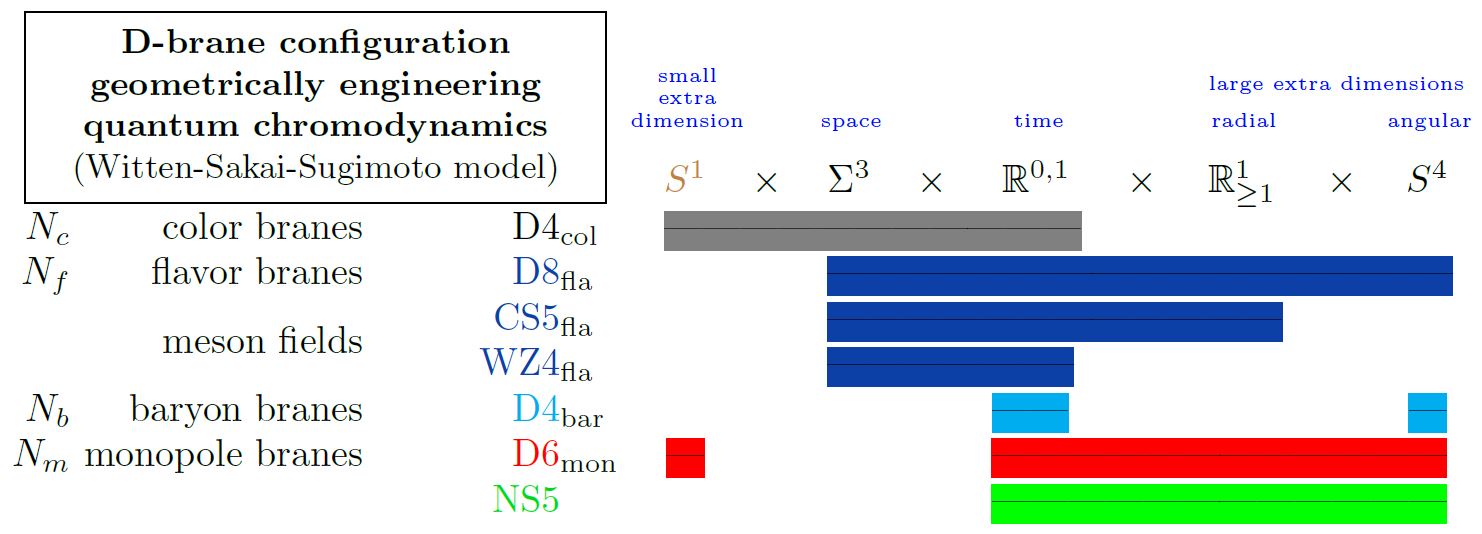
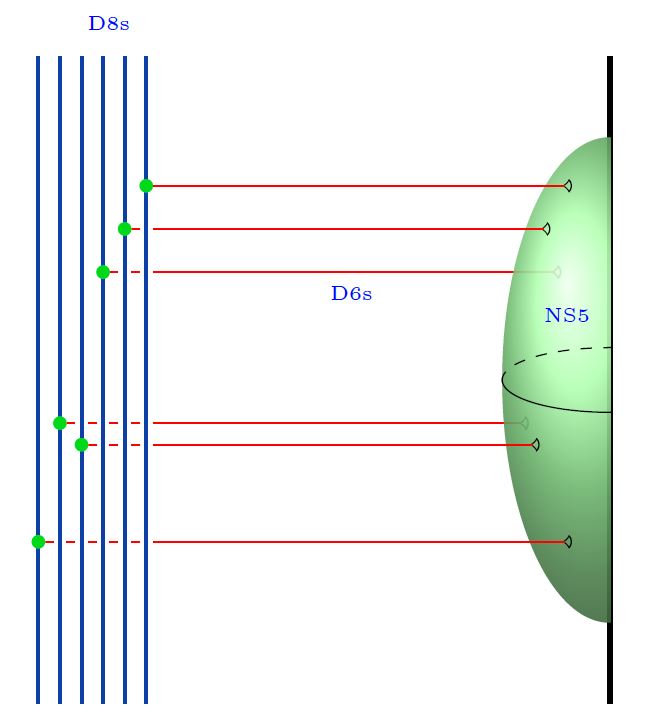
Here we are showing
-
with
-
the 5d Chern-Simons theory on their worldvolume
-
the corresponding 4d WZW model on the boundary
both exhibiting the meson fields;
-
-
(see at WSS-model – Baryons);
-
the Yang-Mills monopole D6-branes
(see at D6-D8-brane bound state);
-
the NS5-branes (often not considered here).
Related concepts
References
General
A good quick account is in
Textbook accounts:
-
Robert E. Marshak, Chapter 3 of: Conceptual Foundations of Modern Particle Physics, World Scientific 1993 (doi:10.1142/1767)
-
Andrzej Buras, Gauge Theory of Weak Decays, (2020) (doi:10.1017/9781139524100, CERN review by Gino Isidori)
Lecture notes:
-
Yuval Grossman, Introduction to flavor physics, CERN Yellow Report CERN-2010-002, pp. 111-144 (arXiv:1006.3534)
-
Benjamin Grinstein, TASI-2013 Lectures on Flavor Physics (arXiv:1501.05283)
-
Yuval Grossman, Philip Tanedo, Just a Taste: Lectures on Flavor Physics, Chapter 4 in: Anticipating the Next Discoveries in Particle Physics (TASI 2016) (arXiv:1711.03624, doi:10.1142/9789813233348_0004)
-
Jure Zupan, Introduction to flavour physics (arXiv:1903.05062)
With an emphasis on CP-violation?:
- Antonio Pich, Flavour Dynamics and Violations of the CP Symmetry, Lectures at the 2017 and 2019 CERN - Latin-American Schools of High-Energy Physics (arXiv:1805.08597)
With an emphasis on the neutrino-sector:
- Zhi-zhong Xing, Flavor structures of charged fermions and massive neutrinos (arXiv:1909.09610)
See also
-
Wikipedia, Flavour (particle physcs)
-
Fernando Abreu de Souza, Gero von Gersdorff, A Random Clockwork of Flavor (arxiv:1911.08476)
On flavour physics and flavour anomalies seen at the LHCb experiment:
-
Niels Tuning, Recent results from LHCb, Nikhef 2020 (nikhef event:2253, pdf, pdf)
In recent years a number of results in flavour physics have drawn some attention due to tensions with respect to Standard Model predictions. An overview of these results will be shown, together with a few recent results from this Spring, both on the flavour anomalies and ‘classical’ flavour physics
Survey and outlook:
-
Riccardo Barbieri, A view of flavour physics in 2021 (arXiv:2103.15635)
-
Vladimir V. Gligorov, Overview of quark flavour results, talk at ICHEP 2022 (Bologna, 2022) [infn:171923, pdf]
The flavour problem
On the flavour problem:
-
Gino Isidori, Kaon decays and the flavour problem, Annales Henri Poincare 4 (2003) S97-S109 (arXiv:hep-ph/0301159)
-
Gino Isidori, The flavor problem, 2016 (pdf, pdf)
-
Wolfgang Altmannshofer, The Flavor Puzzle, Aspen 2014 (pdf, pdf)
In relation to the neutrino mass problem:
- Zhi-zhong Xing, Flavor structures of charged fermions and massive neutrinos Physics Reports Volume 854, 20 April 2020, Pages 1-147 (arXiv:1909.09610, doi:10.1016/j.physrep.2020.02.001)
On the flavor problem in the MSSM:
- Stuart Raby, SUSY Flavor Problem, In: Supersymmetric Grand Unified Theories. Lecture Notes in Physics, vol 939 (doi:10.1007/978-3-319-55255-2_7)
Flavour anomalies
Outlook on the field of flavour physics in view of LHCb-measurement of flavour anomalies and CP violation:
-
Benjamin Grinstein, A path to flavor, talk at Implications of LHCb measurement and future prospects CERN 2019 (pdf, pdf, indico:3582540)
-
Monika Blanke, Flavour Physics from Present to Future Colliders (arxiv:1910.10662)
See also
- Rafael Aoude, Tobias Hurth, Sophie Renner, William Shepherd, The impact of flavour data on global fits of the MFV SMEFT (arXiv:2003.05432)
On flavour physics and potential flavour anomalies in kaon-decays:
-
Andrzej Buras, The Revival of Kaon Flavour Physics, EPJ Web Conf. Volume 129, 2016 (arXiv:1609.05711, doi:10.1051/epjconf/201612900050)
-
Andrzej Buras, The Return of Kaon Flavour Physics, Acta Phys. Pol. B 49, 1043 (2018) (doi:10.5506/APhysPolB.49.1043)
Geometric engineering on flavor branes
The geometric engineering of flavour physics in intersecting D-brane models (flavor branes in AdS/QCD) was originally understood in
- Andreas Karch, Emanuel Katz, Adding flavor to AdS/CFT, JHEP 0206:043, 2002 (arxiv:hep-th/0205236)
and then developed in detail for QCD on D8-branes in the Sakai-Sugimoto model:
-
Tadakatsu Sakai, Shigeki Sugimoto, Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882, 2005 (arXiv:hep-th/0412141)
-
Tadakatsu Sakai, Shigeki Sugimoto, More on a holographic dual of QCD, Prog.Theor.Phys.114:1083-1118, 2005 (arXiv:hep-th/0507073)
-flavor symmetry on heterotic M5-branes
Emergence of SU(2) flavor-symmetry on single M5-branes in heterotic M-theory on ADE-orbifolds (in the D=6 N=(1,0) SCFT on small instantons in heterotic string theory):
-
Abhijit Gadde, Babak Haghighat, Joonho Kim, Seok Kim, Guglielmo Lockhart, Cumrun Vafa, Section 4.2 of: 6d String Chains, J. High Energ. Phys. 2018, 143 (2018) (arXiv:1504.04614, doi:10.1007/JHEP02(2018)143)
-
Kantaro Ohmori, Section 2.3.1 of: Six-Dimensional Superconformal Field Theories and Their Torus Compactifications, Springer Theses 2018 (springer:book/9789811330919)
Argument for this by translation under duality between M-theory and type IIA string theory to half NS5-brane/D6/D8-brane bound state systems in type I' string theory:
Reviewed in:
- Santiago Cabrera, Amihay Hanany, Marcus Sperling, Section 2.3 of: Magnetic Quivers, Higgs Branches, and 6d Theories, JHEP06(2019)071, JHEP07(2019)137 (arXiv:1904.12293)
The emergence of flavor in these half NS5-brane/D6/D8-brane bound state systems, due to the semi-infinite extension of the D6-branes making them act as flavor branes:
-
Amihay Hanany, Alberto Zaffaroni, Branes and Six Dimensional Supersymmetric Theories, Nucl.Phys. B529 (1998) 180-206 (arXiv:hep-th/9712145)
-
Ilka Brunner, Andreas Karch, Branes at Orbifolds versus Hanany Witten in Six Dimensions, JHEP 9803:003, 1998 (arXiv:hep-th/9712143)
Reviewed in:
- Fabio Apruzzi, Marco Fazzi, Section 2.1 of: with orientifolds, J. High Energ. Phys. (2018) 2018: 124 (arXiv:1712.03235)
See also:
- Amihay Hanany, Noppadol Mekareeya, The Small Instanton and the Kraft Procesi Transition, JHEP07 (2018) 098 (arXiv:1801.01129)
Last revised on February 20, 2024 at 09:43:44. See the history of this page for a list of all contributions to it.