nLab adiabatic quantum computation

Idea

By adiabatic quantum computation one means models of quantum computation on parameterized quantum systems where the quantum gates are unitary transformations on a gapped (and possibly topologically ordered) ground state which are induced, via the quantum adiabatic theorem, by sufficiently slow movement of external parameters.

Often the term adiabatic quantum computation is used by default for optimization problems (“quantum annealing”, see the references below).

On the other hand, the possibly most prominent example of adiabatic quantum computation is often not advertized as such (but see CLBFN 2015), namely topological quantum computation by adiabatic braiding of defect anyons (whose positions is the external parameter, varying in a configuration space of points). This is made explicit in Freedman, Kitaev, Larsen & Wang 2003, pp. 6; Nayak, Simon, Stern & Freedman 2008, §II.A.2 (p. 6); and Cheng, Galitski & Das Sarma 2011, p. 1; see also Arovas, Schrieffer, Wilczek & Zee 1985, p. 1 and Stanescu 2020, p. 321; Barlas & Prodan 2020.

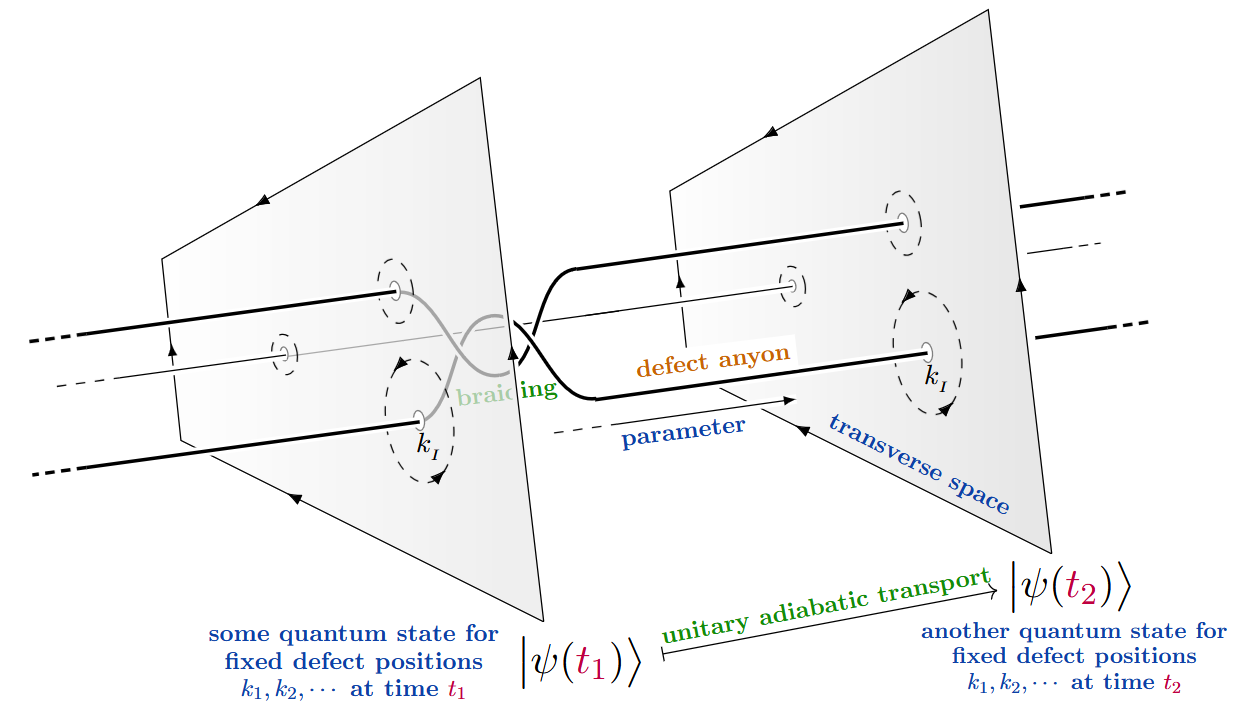
(graphics from SS24)

Related concepts

• quantum adiabatic theorem

• Berry phase

• quantum computation

  • measurement-based quantum computation

  • topological quantum computation

References

General

• Edward Farhi, Jeffrey Goldstone, Sam Gutmann, Michael Sipser, Quantum Computation by Adiabatic Evolution [arXiv:quant-ph/0001106]

• Edward Farhi, Jeffrey Goldstone, Sam Gutmann, Joshua Lapan, Andrew Lundgren, Daniel Preda, A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem, Science 292 5516 (2001) 472-475 [doi:10.1126/science.1057726]

• Dorit Aharonov, Wim van Dam, Julia Kempe, Zeph Landau, Seth Lloyd, Oded Regev, Adiabatic Quantum Computation is Equivalent to Standard Quantum Computation, SIAM Journal of Computing 37 1 (2007) 166-194 [arXiv:quant-ph/0405098, jstor:20454175, doi:10.1109/FOCS.2004.8, doi:10.1137/080734479]

Review:

• Andrew Childs, Overview of adiabatic quantum computation, talk at CIFAR Workshop on Quantum Information Processing (2013) [pdf, pdf]

On robustness of adiabatic quantum computation (such as against decoherence):

• Andrew Childs, Edward Farhi, John Preskill, Robustness of adiabatic quantum computation, Phys.Rev. A 65 (2002) 012322 [arXiv:quant-ph/0108048, doi:10.1103/PhysRevA.65.012322]

In optimization – quantum annealing

Review with focus on optimization problems (quantum annealing):

• Catherine C. McGeoch, Adiabatic Quantum Computation and Quantum Annealing: Theory and Practice Synthesis Lectures on Quantum Computing (2014) [doi:10.2200/S00585ED1V01Y201407QMC008)]

• Tameem Albash, Daniel A. Lidar, Adiabatic Quantum Computing, Rev. Mod. Phys. 90 (2018) 015002 [arXiv:1611.04471, doi:10.1103/RevModPhys.90.015002]

• Salvador E. Venegas-Andraca, William Cruz-Santos, Catherine McGeoch, Marco Lanzagorta, A cross-disciplinary introduction to quantum annealing-based algorithms, Contemporary Physics 59 02 (2018) 174-196 [arXiv:1803.03372, doi:10.1080/00107514.2018.1450720]

• Erica K. Grant and Travis S. Humble, Adiabatic Quantum Computing and Quantum Annealing, Oxford research Encyclopedia (2020) [doi:10.1093/acrefore/9780190871994.013.32]

• Atanu Rajak, Sei Suzuki, Amit Dutta, Bikas K. Chakrabarti, Quantum Annealing: An Overview, Philos Trans A Math Phys Eng Sci 381 2241 (2023) 20210417 [arXiv:2207.01827, doi:10.1098/rsta.2021.0417]

See also:

• Wikipedia, Adiabatic quantum computation

• Kristen L. Pudenz, Tameem Albash, Daniel A. Lidar: Error-corrected quantum annealing with hundreds of qubits, Nature Communications 5 3243 (2014) [doi:10.1038/ncomms4243]

  (with quantum error correction)

• Minjae Jo, Michael Hanks, M. S. Kim, Divide-and-conquer embedding for QUBO quantum annealing [arXiv:2211.02184]

• Yusuke Kimura, Hidetoshi Nishimori, Rigorous convergence condition for quantum annealing, J. Phys. A: Math. Theor. 55 (2022) 435302 [arXiv:2207.12096, doi:10.1088/1751-8121/ac9dce]

A more high-brow mathematical desription via “tangle machines”:

• Avishy Y. Carmi, Daniel Moskovich, §5 of: Tangle Machines, Proc. R. Soc. A 471 (2015) 20150111 [arXiv:1404.2862, doi:10.1098/rspa.2015.0111]

On adiabatic quantum computation combined with parameterized quantum circuits:

• Ioannis Kolotouros, Ioannis Petrongonas, Miloš Prokop, Petros Wallden, Adiabatic quantum computing with parameterized quantum circuits [arXiv:2206.04373]

Geometric phase gates, holonomic quantum computation

References which consider quantum gates operating by (nonabelian) geometric Berry phases due to adiabatic parameter movement (holonomic quantum computation):

• Paolo Zanardi, Mario Rasetti, Holonomic Quantum Computation, Phys. Lett. A 264 (1999) 94-99 [doi:10.1016/S0375-9601(99)00803-8, arXiv:quant-ph/9904011]

• Jiannis Pachos, Paolo Zanardi, Mario Rasetti, Non-Abelian Berry connections for quantum computation, Phys. Rev. A 61 (2000) 010305 [arXiv:quant-ph/9907103, doi:10.1103/PhysRevA.61.010305]

• Jonathan A. Jones, Vlatko Vedral, Artur Ekert, Giuseppe Castagnoli, Geometric quantum computation using nuclear magnetic resonance, Nature 403 (2000) 869–871 [doi:10.1038/35002528]

• Giuseppe Falci, Rosario Fazio, G. Massimo Palma, Jens Siewert & Vlatko Vedral, Detection of geometric phases in superconducting nanocircuits, Nature 407 355–358 (2000) [doi:10.1038/35030052]

• Jiannis Pachos, Paolo Zanardi, Quantum Holonomies for Quantum Computing, Int. J. Mod. Phys. B 15 (2001) 1257-1286 [arXiv:quant-ph/0007110, doi:10.1142/S0217979201004836]

• L. M. Duan, J. I. Cirac, P. Zoller, Geometric Manipulation of Trapped Ions for Quantum Computation, Science 292 (2001) 1695 [arXiv:quant-ph/0111086, doi:10.1126/science.1058835]

• Jiang Zhang, Thi Ha Kyaw, Stefan Filipp, Leong-Chuan Kwek, Erik Sjöqvist, Dianmin Tong, Geometric and holonomic quantum computation, Physics Reports 1027 (2023) 1-53 [arXiv:2110.03602, doi:10.1016/j.physrep.2023.07.004]

• Daniel Turyansky et al., Inertial geometric quantum logic gates, Physical Review Applied 21 054033 (2024) [arXiv:2303.13674, doi:10.1103/PhysRevApplied.21.054033]

• Logan W. Cooke et al., Demonstration of Floquet engineered non-Abelian geometric phase for holonomic quantum computing, Phys. Rev. Research 6 013057 (2024) [arXiv:2307.12957, doi:10.1103/PhysRevResearch.6.013057]

Realization of non-abelian holonomy on degenerate ground states in photonic waveguide arrays:

• Julien Pinske, Lucas Teuber, Stefan Scheel: Highly degenerate photonic waveguide structures for holonomic computation, Phys. Rev. A 101 062314 (2020) [doi:10.1103/PhysRevA.101.062314]

• Vera Neef, Julien Pinske, Friederike Klauck, Lucas Teuber, Mark Kremer et al.: Experimental Realization of a non-Abelian $U(3)$ Holonomy, in: 2021 Conference on Lasers and Electro-Optics (CLEO), IEEE (2021) [ieee:9572414]

• Julien Pinske, Stefan Scheel, Symmetry-protected non-Abelian geometric phases in optical waveguides with nonorthogonal modes, Phys. Rev. A 105 013507 (2022) [doi:10.1103/PhysRevA.105.013507, arXiv:2105.04859]

• Vera Neef, Julien Pinske, Friederike Klauck, Lucas Teuber, Mark Kremer, Max Ehrhardt, Matthias Heinrich, Stefan Scheel Alexander Szameit: Three-dimensional non-Abelian quantum holonomy, Nat. Phys. 19 (2023) 30–34 [doi:10.1038/s41567-022-01807-5]

In topological quantum computation

References which make explicit that topological quantum computation by braiding of anyon worldlines is a form of adiabatic quantum computation:

• Daniel P. Arovas, Robert Schrieffer, Frank Wilczek, Anthony Zee, Statistical mechanics of anyons, Nuclear Physics B 251 (1985) 117-126 (reprinted in Wilczek 1990, p. 173-182) [doi:10.1016/0550-3213(85)90252-4]

• Childs, Farhi & Preskill (2002), p. 2

• Michael Freedman, Alexei Kitaev, Michael Larsen, Zhenghan Wang, pp. 6 of Topological quantum computation, Bull. Amer. Math. Soc. 40 (2003) 31-38 [arXiv:quant-ph/0101025, doi:10.1090/S0273-0979-02-00964-3, pdf]

• Nicholas E. Bonesteel, Layla Hormozi, Georgios Zikos, Steven H. Simon, p. 1 of: Braid Topologies for Quantum Computation, Phys. Rev. Lett. 95 140503 (2005) [arXiv:quant-ph/0505065, doi:10.1103/PhysRevLett.95.140503]

• Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, Sankar Das Sarma, §II.A.2 (p. 6) of: Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80 1083 (2008) [arXiv:0707.1888, doi:10.1103/RevModPhys.80.1083]

• Meng Cheng, Victor Galitski, Sankar Das Sarma, Non-adiabatic Effects in the Braiding of Non-Abelian Anyons in Topological Superconductors, Phys. Rev. B 84 (2011) 104529 [arXiv:1106.2549, doi:10.1103/PhysRevB.84.104529]

• Gustavo Rigolin, Gerardo Ortiz, p. 1 of: The Adiabatic Theorem for Quantum Systems with Spectral Degeneracy, Phys. Rev. A 85 062111 (2012) [arXiv:1111.5333, doi:10.1103/PhysRevA.85.062111]

• Jiannis K. Pachos, Introduction to Topological Quantum Computation, Cambridge University Press (2012) [doi:10.1017/CBO9780511792908]

  [p. 50]: “topological quantum computation resembles an adiabatic quantum computation with constant energy gap, where the quasiparticle coordinates provide the control parameters of the Hamiltonian.”

  [p. 52]: “Holonomic quantum computation resembles the adiabatic scheme […] topological quantum computation can be considered as holonomic computation where the employed adiabatic evolutions have topological characteristics.”

• Chris Cesare, Andrew J. Landahl, Dave Bacon, Steven T. Flammia, Alice Neels, Adiabatic topological quantum computing, Phys. Rev. A 92 (2015) 012336 [arXiv:1406.2690, doi:10.1103/PhysRevA.92.012336]

• Ville Lahtinen, Jiannis K. Pachos, p. 1 of: A Short Introduction to Topological Quantum Computation, SciPost Phys. 3 021 (2017) [arXiv:1705.04103, doi:10.21468/SciPostPhys.3.3.021]

• E. Macaluso, T. Comparin, L. Mazza, and I. Carusotto, Fusion Channels of Non-Abelian Anyons from Angular-Momentum and Density-Profile Measurements, Phys. Rev. Lett. 123 266801 (2019) [arXiv:1903.03011, doi:10.1103/PhysRevLett.123.266801]

• Tudor D. Stanescu, p. 321 of: Introduction to Topological Quantum Matter & Quantum Computation, CRC Press 2020 (ISBN:9780367574116)

• Yafis Barlas, Emil Prodan, Topological braiding of non-Abelian mid-gap defects in classical meta-materials, Phys. Rev. Lett. 124 (2020) 146801 [arXiv:1903.00463, doi:10.1103/PhysRevLett.124.146801]