nLab electromagnetic field
Context
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Differential cohomology
Ingredients
Connections on bundles
Higher abelian differential cohomology
Higher nonabelian differential cohomology
Fiber integration
Application to gauge theory
Contents
Idea
The electromagnetic field is is a gauge field which unifies the electric field and the magnetic field. A configuration of the electromagnetic field on a space in the absence of magnetic charge is modeled by a cocycle in degree 2 ordinary differential cohomology.
This may be realized in particular equivalently by
-
a -principal bundle with connection on ;
-
a degree 2 Deligne cocycle on .
In the presence of magnetic charge the electromagnetic field is modeled by a cocycle in differential twisted cohomology, where the twist is given by the differential 3-cocycle that models the magnetic current.
The analogous field modeled by a degree 3 Deligne cocycle is the Kalb-Ramond field.
History
…historical section eventually goes here..
…electricity and magnetism were discovered independently, Maxwell's equations in classical vector analysis which allows the formulation as a tensor as below, and “magnetism is a consequence of electrostatics and covariance, hence the composite noun electromagnetism”…
(…)
Mathematical model from physical input
The electromagnetic field is modeled by a circle bundle with connection.
We describe how this identification arises from experimental input.
The input is two-fold
-
Maxwell’s equations say that (using the experimentally observed absence of net magnetic charge) the field strength of electromagnetism is a closed differential 2-form on spacetime;
-
The Dirac charge quantization argument shows that in order for the electromagnetic field to serve as the background gauge field to which a charged quantum mechanical particle couples (for instance an electron), it must be true that this 2-form is the curvature 2-form of a circle bundle with connection.
We say this now in more detail.
Maxwell’s equations
We first discuss in Field strength as a closed 2-form how Maxwell's equations state that the electromagnetic field strength is a closed differential 2-form on spacetime
Field strength is a closed 2-form
In modern language, the insight of (Maxwell, 1865) is that locally, when physical spacetime is well approximated by a patch of its tangent space, i.e. by a patch of 4-dimensional Minkowski space , the electric field and magnetic field combine into a differential 2-form – the Faraday tensor
in and the electric charge density and current density combine to a differential 3-form
in such that the following two equations of differential forms are satisfied
where is the de Rham differential operator and the Hodge star operator. If we decompose into its components as before as
then in terms of these components the field equations – called Maxwell’s equations – read as follows.
-
magnetic Gauss law:
-
Faraday’s law:
-
Gauss’ law:
-
Ampère’s law
Vector potential – as a Cech-Deligne 2-cocycle
By the above, the electromagnetic field strength (in the absence of net magnetic charge) on spacetime is given by a 2-form and an electric current 3-form satisfying Maxwell’s equations
The first equation with the Poincare lemma implies that one may find
-
on a good open cover of by open subsets
-
a collection of differential 1-forms, such that
-
and a collection of real valued functions on double overlaps such that
The forms are called a vector potential or the electromagnetic potential for the electromagnetic field.
Notice that it follows that on triple overlaps we have
which means that on that overlap the function
is constant. If one requires these constants all to be inside a discrete subgroup , then the data defines a degree 2-cocycle in Cech-Deligne cohomology on with coefficients in . Below we see that experiment demands that such a subgroup exists and is given by the additive group of integers.
Kirchhoff’s laws
Kirchhoff's laws are a kind of coarse graining of Maxwell’s equations, where instead of infinitesimal quantities one considers actual macroscopic current and voltage.
Background gauge field for charge quantum
The exponentiated action functional for the sigma model describing a particle on target space charged under an electromagnetic background gauge field has to satisfy two properties:
-
It must be given by the holonomy of the 1-forms (this encodes, via variational calculus, the Lorentz force exerted by the electromagnetic field on the particle ):
-
It must take values in the circle group (this is a basic rule of the quantum mechanics describing the particle):
Therefore the above data is subject to the additional constraint that it induces well-defined -valued holonomy – this is Dirac’s quantization condition, a necessary requirement for the existence of quantum mechanical particles on that are charged under the background electromagnetic field.
Concretely: for any smooth curve and any cover of refining the pullback of the cover to , and for every triangulation of subordinate to , i.e. such that there is an index map such that and
the expression
(where if is the final vertex of and otherwise)
has to be a well defined element in (independent of all the choices made).
This implies in particular that cancelling from the triangulation an edge of vanishing length must have no effect on the formula, which in turn means that for all we have
and hence
In short: the holonomy of the constant path on a point must be , but if that path sits in a triple intersection then the holonomy is equivalently given as the exponentiated sum of the three transition functions. This forces the sum to land in .
In total this says precisely that the data
is a Čech cocycle with coefficients in the degree 2 Deligne complex whose curvature2-form is the given Maxwell curvature 2-form.
Charge quantization
See at Dirac charge quantization.
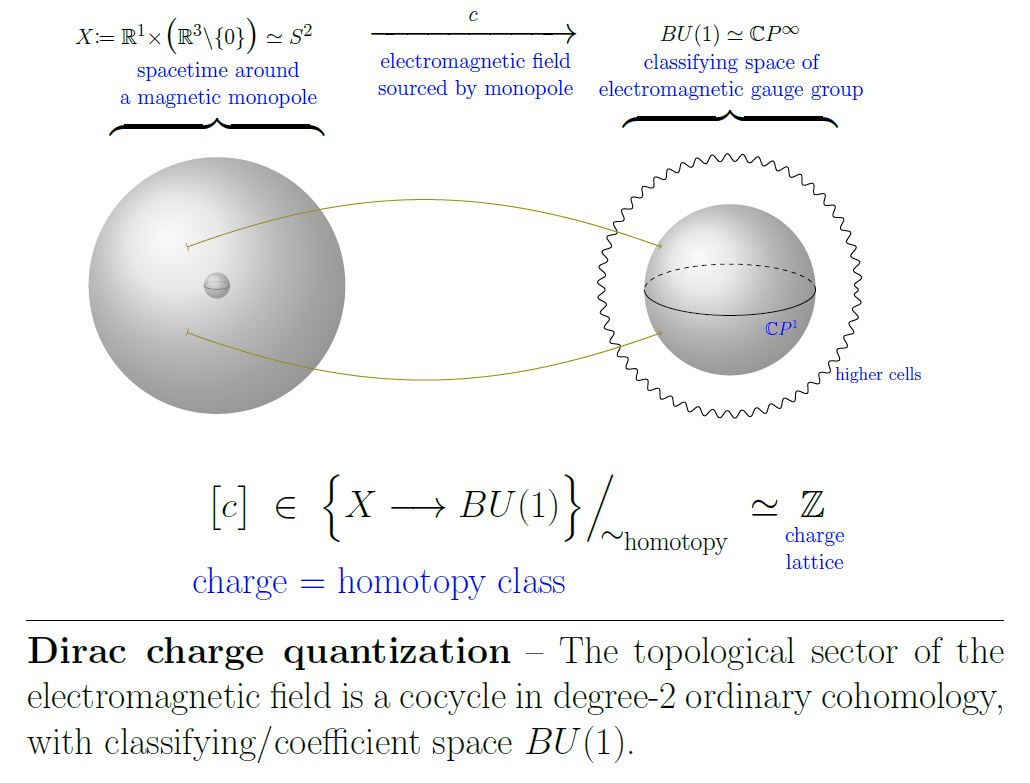
Dirac’s original argument
under construction
Dirac originally presented the following reasoning, which captures the main point of the above considerations.
He considered to be without the origin,
which is a manifold of the topology of (weakly homotopy equivalent to) the 2-sphere .
He imagined a situation with a magnetic charge supported on the point located at the origin and removed that point in order to keep the field strength to be a closed 2-form on all of .
(Indeed, if one does not remove the support of magnetic charge, the argument becomes much more sophisticated and involves higher differential cocycles given by bundle gerbes. This was not understood before Dan Freed’s Dirac charge quantization and generalized differential cohomology.)
Then he considered a single coordinate patch
given by minus the right half of the first coordinate axis.
Traditionally physicists try to give that half-line a physical interpretation by imagining that it is the body of an idealized infinitely-thin and to one side infinitely-long solenoid. Indeed, such a solenoid would have a magnetic monopole charge on each of its ends, so if the one end is imagined to have disappeared to infinity, then the other one is the magnetic charge that Dirac imagines to sit at the origin of our setup.
In this context the half-line is called a Dirac string. While there is the possibility to sensibly discuss the idea that this Dirac string actually models a physical entity like an idealized solenoid, its main purpose historically is to confuse physics students and keep them from understanding the theory of fiber bundles (see at fiber bundles in physics). Therefore here we shall refrain from talking about Dirac strings and consider as exactly what it is, by itself: an open subset that is part of a cover of . Unfortunately, of course, Dirac didn’t mention the other open subsets in that cover (at least one more is needed for a decent discussion), so that the Dirac string keeps haunting physicists.
…running out of time…just quickly now…
…Dirac effectively considered the overlap cocycle condition , found that by the requirement that has well defined holonomy it follows that there must be a function with values in such that , then did away with the -patch (considering a kind of limit as we encircle the half axis) and concluded that must be the log-differential of a -valued function, whose winding number around the half-axis he identified with the magnetic charge, which in terms of bundles one identifies with the Chern-class of the bundle in question …
…have to run…
In modern terms:
The clutching construction gives -principal bundle ob by covering with two hemispheres and and picking a transition function on the overlap . The integral winding number of represents the first Chern class of the line bundle.
By the standard formula for existence of principal connections on given principal bundles, given a choice of partition of unity then the connection on is given by
If we think (as we may) of as covering most of the 2-sphere except one point and of the -open neighbourhood of that point, then this vanishes on most of the sphere and close to the point taken out (“the Dirac string”) it becomes non-vanishing and equal to .
Electric-magnetic charge quantization
Suppose we had a circle bundle with connection on a bundle representing an electromagnetic field with net magnetic charge given by some magnetic current
that is supported in some compact spatial region with boundary sphere .
by the Stokes theorem. It follows from the fact that is the curvature 2-form on a circle bundle that is integral: it is given by the first Chern class of the bundle.
(…)
For a closed but contractible trajectory of an electrically charged particle, the action functional is
by the Stokes theorem, for some 2-disk cobounding the circle. If now approaches a constant path and the 2-disk is taken to wrap the 2-cycle , then this becomes
Which implies that with the magnetic charge being quantized, also the electric charge is.
(…)
Related concepts
References
See also the references at electromagnetism:
Maxwell's equations originate in:
- James Clerk Maxwell, A Dynamical Theory of the Electromagnetic Field, Philosophical Transactions of the Royal Society of London 155, 459–512 (1865).
Dirac's charge quantization argument appeared in
- P.A.M. Dirac, Quantized Singularities in the Electromagnetic Field, Proceedings of the Royal Society, A133 (1931) pp 60–72.
Review:
- Theodore Frankel, section 5.5 of: The Geometry of Physics - An Introduction, Cambridge University Press (1997, 2004, 2012) [doi:10.1017/CBO9781139061377, webpage]
Discussions of the basic geometry behind Maxwell equations can be found in
- Hong-Mo Chan, Sheung Tsun Tsou, Some elementary gauge theory concepts, gBooks
- Gregory L. Naber, Topology, geometry, and gauge fields: interactions
- Differential Forms in Electromagnetic Theory
For undergraduate lectures including experimental material see
- Walter Lewin, Electricity and magnetism, 2002, MIT opencourseware
The Lorentz-invariants of the electromagnetic field:
- C. A. Escobar, L. F. Urrutia, The invariants of the electromagnetic field, Journal of Mathematical Physics 55, 032902 (2014) (arXiv:1309.4185)
Last revised on April 23, 2025 at 00:37:29. See the history of this page for a list of all contributions to it.