nLab gauged supergravity
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
Contents
Idea
Theories of supergravity in dimension always contain a global symmetry called R-symmetry (a remnant of the full 11-dimensional supergravity -symmetry after KK-compactification). In some cases this is promoted to a local symmetry, such that there is a gauge field (connection on a bundle) with coefficients in that group. These are called gauged supergravity theories.
Properties
From dimensional reduction
In many cases, gauged supergravity theories are obtained by dimensional reduction from 11-dimensional supergravity or type II supergravity, which themselves do not contain a gauge field but higher degree fields (“fluxes”), the supergravity C-field and the B-field respectively. These induce gauged supergravities (e.g. Samtleben 08, figure 1). The gauge groups are the U-duality groups of the compactification (e.g. Samtleben 08, table 1).
From double and exceptional field theory
Exceptional field theory (but also double field theory) reduces to gauged supergravity under generalized Scherk-Schwarz reduction, i.e. a dimensional reduction combined with U-duality (or just T-duality) twists.
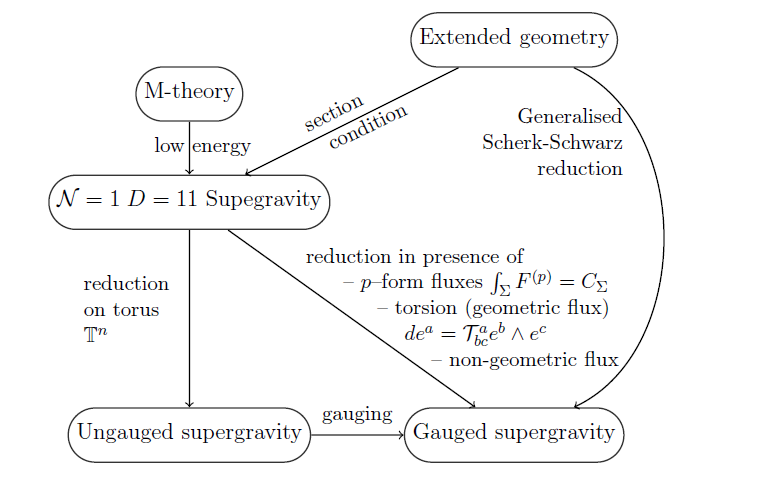
Examples
Some examples are discussed at
Related concepts
References
Review:
-
Diederik Roest: M-theory and Gauged Supergravities, Fortsch. Phys. 53 (2005) 119-230 [arXiv:hep-th/0408175, doi:10.1002/prop.200410192]
-
Martin Weidner, Gauged Supergravities in Various Spacetime Dimensions, Fortsch.Phys. 55 843-945 (2007) [arXiv:hep-th/0702084]
-
Henning Samtleben, Lectures on Gauged Supergravity and Flux Compactifications [arXiv:0808.4076]
-
Mario Trigiante, Gauged Supergravities, Physics Reports 680 (2017) 1-175 [arXiv:1609.09745, doi:10.1016/j.physrep.2017.03.001]
Discussion of the origin in KK-compactification of 11-dimensional supergravity/M-theory is in
- Diederik Roest, M-theory and Gauged Supergravities, Fortsch.Phys.53:119-230,2005 (arXiv:hep-th/0408175)
Maximally gauged D=4 supergravity was first discussed in
- Bernard de Wit, Hermann Nicolai, supergravity, Nucl. Phys. B 208 (1982) 323
and gauged D=5 supergravity in
-
Murat Günaydin, L. J. Romans and Nicholas Warner, Gauged Supergravity in Five Dimensions, Phys. Lett. 154B, (1985) 268 (spire:207663, doi:10.1016/0370-2693(85)90361-2)
-
Murat Günaydin, L. J. Romans and Nicholas Warner, Compact and Non–Compact Gauged Supergravity Theories in Five Dimensions, Nucl. Phys. B272 (1986) 598 (spire:219727, doi:10.1016/0550-3213(86)90237-3)
-
M. Pernici, K. Pilch, Peter van Nieuwenhuizen, Gauged Supergravity, Nucl.Phys. B259 (1985) 460 (spire)
Discussion in the context of flux compactification of type II superstring theory includes
- Mariana Graña, section 5.3 of Flux compactifications in string theory: a comprehensive review, Phys.Rept. 423 (2006) 91-158 (arXiv:hep-th/0509003)
Discussion in the context of the D'Auria-Fré formulation of supergravity is in
- Pietro Fré, M-theory FDA, Twisted Tori and Chevalley Cohomology, Nucl.Phys.B742:86-123, 2006 (arXiv:hep-th/0510068)
Discussion related to orbifold singularities includes
- Richard Corrado, Murat Gunaydin, Nicholas P. Warner, Marco Zagermann, Orbifolds and Flows from Gauged Supergravity, Phys.Rev.D65:125024,2002 (arXiv:hep-th/0203057)
Review of the relation with double field theory and exceptional field theory:
- Edvard Musaev, U-dualities in Type II string theories and M-theory, Symmetry 2019, 11(8), 993 (arXiv:1311.3331, doi:10.3390/sym11080993)
Last revised on September 17, 2024 at 09:49:54. See the history of this page for a list of all contributions to it.