nLab D=5 supergravity
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
supergravity in dimension 5. For this arises from 11-dimensional supergravity by KK-compactification on a Calabi-Yau manifold of complex dimension 3 (see at M-theory on Calabi-Yau manifolds), hence serves as the low-energy effective field theory of the strong-coupling version of Calabi-Yau compactifications of type IIA string theory (see supersymmetry and Calabi-Yau manifolds)
Properties
5d Chern-Simons term
This theory has a 2-form field strength , locally , with a 5d Chern-Simons theory action functional locally of the form (e.g. Castellani-D’Auria-Fre (III.5.70), Gauntlet-Myers-Townsend 98, p. 3, GGHPR 02 (2.1), Bonetti-Grimm-Hohenegger 13). Hence its equation of motion is of the non-linear form
with the Hodge dual of (GGHPR 02 (2.2)).
This is reflected in the corresponding cochains on super Minkowski spacetime
satisfying
due to the Fierz identity in Castellani-D’Auria-Fré 91 (III.5.50a), this example:
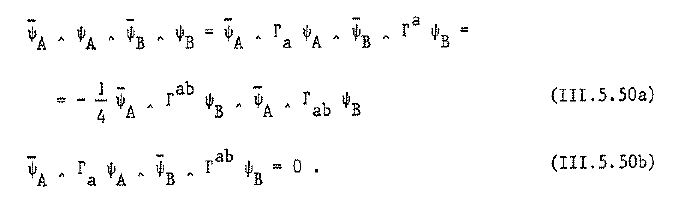
(the other Fierz identity (III.5.50a) gives the cocycle for the membrane (super 2-brane in 5d) , , that appears already in the old brane scan. )
This is a lower dimensional analogue to the situation for the C-field (locally ) in 11-dimensional supergravity, which has a Chern-Simons term locally of the form and hence the equation of motion
with .
Black holes and black rings
The first black ring solution in 5d sugra was found in (Elvang-Emparan-Mateos-Reall 04, Elvang-Emparan-Mateos-Reall 05).
Supersymmetric black holes exist precisely only in dimensions 4 and 5 (Gauntlett-Myers-Townsend 98). These play a key role in the discussion of black holes in string theory.
(There are supersymmetric particle-like solutions of supergravity theories that are sometimes called black holes, but these are always singular. There are also supersymmetric black holes in , but the spacetime in that case is asymptotically anti-de Sitter spacetime rather than asymptotically flat. Of course, there are non-singular supersymmetric black brane solutions in various supergravity theories but these are neither ‘particle-like’ nor, strictly speaking, asymptotically flat.)
Via Calabi-Yau compactification of 11d supergravity
Discussion of 5d supergravity as a KK-compactification of 11-dimensional supergravity on a Calabi-Yau manifold of complex dimension 3 (M-theory on Calabi-Yau manifolds) is discussed in
(Hull-Townsend 95, p.30-31, Cadavid-Ceresole-D’Auria-Ferrara 95 Ferrara-Khuria-Minasian 96, Ferrara-Minasian-Sagnotti 96). See also (Mizoguchi-Ohta 98).
U-duality
supersymmetry
Consider super Lie algebra cocoycles on 5d super-Minkowski spacetime (as in the brane scan).
With the notation as used at super Minkowski spacetime – Canonical coordinates, there are now two copies of spinor-valued 1-forms, denoted and . We use indices of the form for these. Then the non-trivial bit of the Chevalley-Eilenberg algebra differential for , super Minkowski spacetime is
where summation over repeated indices is understood.
There is a Fierz identity
(Castellani-D’Auria-Fré (III.5.50a))
This implies that
There is a 4-cocycle of the form
(Castellani-D’Auria-Fré (III.5.50b), (III.5.53c))
Related concepts
-
10-dimensional type II supergravity, heterotic supergravity
References
Construction of 5d gauged supergravity via D'Auria-Fré formulation of supergravity is in
- Laura Andrianopoli, Francesco Cordaro, Pietro Fré, Leonardo Gualtieri, Non-Semisimple Gaugings of D=5 N=8 Supergravity and FDA.s, Class. Quant. Grav. 18 (2001) 395-414 [arXiv:hep-th/0009048]
surveyed in
- Laura Andrianopoli, Francesco Cordaro, Pietro Fré, Non-Semisimple Gaugings of D=5 N=8 Supergravity, Fortsch.Phys.49:511-518,2001 (arXiv:hep-th/0012203)
General
General discussion:
-
Leonardo Castellani, Riccardo D'Auria, Pietro Fré, chapter III.5 of Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991)
-
William Linch III, Markus A. Luty, J. Phillips, Five dimensional supergravity in superspace, Phys.Rev.D68:025008,2003 (arXiv:hep-th/0209060)
-
Jerome Gauntlett, Jan Gutowski, Christopher Hull, Stathis Pakis, Harvey Reall, All supersymmetric solutions of minimal supergravity in five dimensions, Class. Quant. Grav. 20 (2003) 4587-4634 [arXiv:hep-th/0209114, doi:10.1088/0264-9381/20/21/005]
-
Sorin Cucu, From M-theory to supergravity and duality-symmetric theories (arXiv:hep-th/0310105)
-
Eric Bergshoeff, Sorin Cucu, Tim de Wit, Jos Gheerardyn, Stefan Vandoren, Antoine Van Proeyen, supergravity in five dimensions revisited (arXiv:hep-th/0403045)
-
Katrin Becker, Melanie Becker, Daniel Butter, William Linch III, Stephen Randall: Five-dimensional Supergravity in Superspace, J. High Energ. Phys. 2020 98 (2020) [arXiv:1909.09208, doi:10.1007/JHEP03(2020)098]
-
Edoardo Lauria, Antoine Van Proeyen, Supergravity in Dimensions (arXiv:2004.11433)
See also:
-
Andrew Beckett, José Figueroa-O'Farrill, Killing superalgebras for lorentzian five-manifolds (arxiv:2105.05775)
-
Soumya Adhikari, Bindusar Sahoo, conformal supergravity in five dimensions* [arXiv:2312.01879]
Via M-theory on Calabi-Yau 3-folds
Discussion via KK-compactification as M-theory on Calabi-Yau manifolds includes
-
Chris Hull, Paul Townsend, pages 30 and 31 of Unity of Superstring Dualities, Nucl.Phys.B438:109-137,1995 (arXiv:hep-th/9410167)
-
{CadavidCeresoleDAuriaFerrara95} A.C. Cadavid, A. Ceresole, Riccardo D'Auria, Sergio Ferrara, 11-Dimensional Supergravity Compactified on Calabi-Yau Threefolds (arXiv:hep-th/9506144)
-
Sergio Ferrara, Ramzi R. Khuria, Ruben Minasian, M-theory on a Calabi-Yau manifold, Phys.Lett.B375:81-88,1996 (arXiv:hep-th/9602102)
-
Sergio Ferrara, Ruben Minasian, Augusto Sagnotti, Low-Energy Analysis of M and F Theories on Calabi-Yau Threefolds, Nucl.Phys. B474 (1996) 323-342 (arXiv:hep-th/9604097)
-
S. Mizoguchi, N. Ohta, More on the Similarity between Simple Supergravity and M Theory, Phys.Lett. B441 (1998) 123-132 (arXiv:hep-th/9807111)
Further discussion of the 5d Chern-Simons term includes
- Federico Bonetti, Thomas Grimm, Stefan Hohenegger, One-loop Chern-Simons terms in five dimensions (arXiv:1302.2918)
(one-loop corrections).
Via type IIB theory
- Arnaud Baguet, Olaf Hohm, Henning Samtleben, Consistent Type IIB Reductions to Maximal 5D Supergravity (arXiv:1506.01385)
Gauged sugra
The maximal 5d gauged supergravity was first constructed in
-
M. Pernici, K. Pilch, Peter van Nieuwenhuizen, Gauged Supergravity, Nucl.Phys. B259 (1985) 460 (spire)
-
Murat Günaydin, L. J. Romans and Nicholas Warner, Gauged Supergravity in Five Dimensions, Phys. Lett. 154B, (1985) 268 (spire:207663, doi:10.1016/0370-2693(85)90361-2)
-
Murat Günaydin, L. J. Romans and Nicholas Warner, Compact and Non–Compact Gauged Supergravity Theories in Five Dimensions, Nucl. Phys. B272 (1986) 598 (spire:219727, doi:10.1016/0550-3213(86)90237-3)
See (ACFG 01).
-
Murat Gunaydin, Marco Zagermann, The Gauging of Five-dimensional, Maxwell-Einstein Supergravity Theories coupled to Tensor Multiplets, Nucl.Phys.B572:131-150,2000 (arXiv:hep-th/9912027)
-
Murat Gunaydin, Marco Zagermann, The Vacua of 5d, Gauged Yang-Mills/Einstein/Tensor Supergravity: Abelian Case, Phys.Rev.D62:044028,2000 (arXiv:hep-th/0002228)
-
A. Ceresole, Gianguido Dall'Agata, General matter coupled , gauged supergravity, Nucl.Phys. B585 (2000) 143-170 (arXiv:hep-th/0004111)
-
John Ellis, Murat Gunaydin, Marco Zagermann, Options for Gauge Groups in Five-Dimensional Supergravity, JHEP 0111:024,2001 (arXiv:hep-th/0108094)
Horava-Witten compactification
Discussion of KK-compactification on -orbifolds (the version of Horava-Witten theory after dimensional reduction) is discussed in
- Filipe Paccetti Correia, Michael G. Schmidt, Zurab Tavartkiladze, 4D Superfield Reduction of 5D Orbifold SUGRA and Heterotic M-theory (arXiv:hep-th/0602173)
Black hole solutions
Discussion of lifts of 4d black holes to 5d black holes and black rings and embedding as black holes in string theory includes
-
Jerome Gauntlett, Robert C. Myers, Paul Townsend, Black Holes of Supergravity, Class.Quant.Grav. 16 (1999) 1-21 [arXiv:hep-th/9810204, doi:10.1088/0264-9381/16/1/001]
-
Henriette Elvang, Roberto Emparan, David Mateos, Harvey Reall, A supersymmetric black ring, Phys. Rev. Lett. 93:211302,2004 (arXiv:hep-th/0407065)
-
Henriette Elvang, Roberto Emparan, David Mateos, Harvey Reall, Supersymmetric 4D Rotating Black Holes from 5D Black Rings, JHEP0508:042,2005 (arXiv:hep-th/0504125)
-
Iosif Bena, Per Kraus, Microscopic description of black rings in AdS/CFT JHEP 12 (2004) 070 (hep-th/0408186)
-
Iosif Bena, Per Kraus, Microstates of the D1-D5-KK system Phys. Rev. D72 (2005) 025007 (hep-th/0503053)
-
Davide Gaiotto, Andrew Strominger, Xi Yin, 5D black rings and 4D black holes JHEP 02 (2006) 023 (hep-th/0504126)
-
Davide Gaiotto, Andrew Strominger, Xi Yin, New connections between 4D and 5D black holes, JHEP 02 (2006) 024 (hep-th/0503217)
-
Alejandra Castro, Joshua L. Davis, Per Kraus, Finn Larsen, String Theory Effects on Five-Dimensional Black Hole Physics (arXiv:0801.1863)
Review:
-
Per Kraus, Lectures on black holes and the / correspondence (arXiv:hep-th/0609074)
Stringy black holes in five dimensions, 2007 (pdf slides)
Further defect branes:
-
Eun Kyung Park, Pyung Seong Kwon, NS-branes in 5d brane world models, Phys. Rev. D82:046001, 2010 (arXiv:1007.1290, doi:10.1103/PhysRevD.82.046001)
-
Minkyu Park, Masaki Shigemori, Codimension-2 Solutions in Five-Dimensional Supergravity, JHEP 1510 (2015) 011 (arXiv:1505.05169)
-
Masaki Shigemori, Interpolating between multi-center microstate geometries, JHEP 09 (2021) 010 (arXiv:2105.11639)
Last revised on November 3, 2024 at 09:35:59. See the history of this page for a list of all contributions to it.