nLab D-brane charge quantization in K-theory
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Cohomology
Special and general types
-
group cohomology, nonabelian group cohomology, Lie group cohomology
-
-
cohomology with constant coefficients / with a local system of coefficients
Special notions
Variants
-
differential cohomology
Extra structure
Operations
Theorems
Contrents
Idea
Statement
A famous conjecture in non-perturbative string theory says (Minasian-Moore 97, Witten 98, reviewed in Witten 00, Moore 02, Manjarín 04, Evslin 06, Fredenhagen 08) that D-brane charge and RR-field fluxes are quantized in the Whitehead-generalized cohomology theory known as topological K-theory, specifically in KU-cohomology for type II string theory and more generally in KR cohomology theory in the presence of orientifolds, reducing to KO-cohomology in type I string theory right on the O-planes.
More generally, the conjecture says that the fluxes of the NS B-field and of the RR-fields are jointly flux-quantized in twisted topological K-theory, with the B-field constituting the twist.
Yet more generally, the conjecture says that, over orbifolds, the charge quantization is in orbifold K-theory, hence in equivariant K-theory for the usual global quotient orbifolds, hence in twisted equivariant K-theory for the combined B-field/RR-fields. A sketch of how to state this more precisely is in Distler-Freed-Moore 09.
This means, or would mean, that the full massless physical fields in type II string theory, including their higher “gauge potentials”, are cocycles in a differential cohomology-version of these twisted generalized cohomology theories, hence in differential K-theory if the B-field is ignored, in twisted differential K-theory if the B-field is included, and in twisted equivariant differential K-theory if also orbifolds are taken into account.
Motivation
An immediate way to motivate the conjecture is to notice that the image of the -twisted Chern character on twisted K-theory (say in degree 0, hence in type IIA string theory, for definitess)

takes values in -twisted de Rham cohomology, whose cocycles are collections of differential forms satisfying exactly the Bianchi identities
expected of the B-field flux and the RR-field fluxes . This is ultimately what underlies the observation in Minasian-Moore 97, as brought out clearly in Brodzki-Mathai-Rosenberg-Szabo 06.
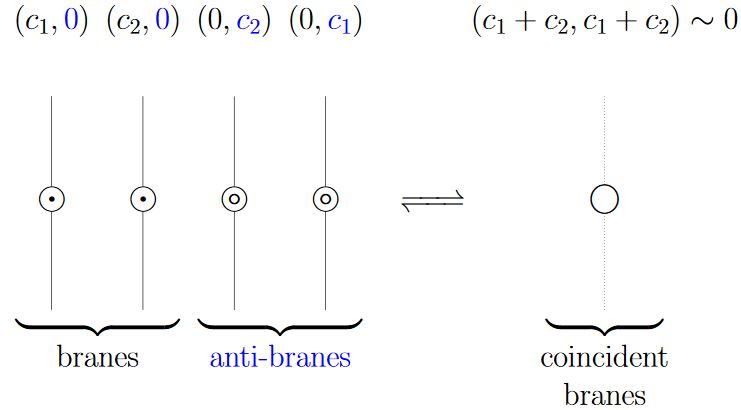
A conceptual picture of why topological K-theory would capture D-brane charge was suggested in Witten 98, Section 3: The tachyon condensation expected (this is Sen's conjecture from Sen 98) for open strings between D-brane/anti-D-branes plausibly implements on their Chan-Paton vector bundles the defining equivalence relation (here) of topological K-theory, as indicated in the figure.
While plausible and widely accepted in the string theory folklore, this picture remains to be checked (see below).
Open problems
While the conjecture that D-brane charge is in K-theory has become widely accepted folklore in much of the string theory-community, it remains unproven – just as many and most folklore-statements involving non-perturbative brane-physics, not the least because an actual theory of non-perturbative string theory (aka M-theory) remains missing (see also at M-theory – the open problem).
Moreover, there are a number of indications that the conjecture can not actually be true without some modification, as in parts it seems to be in contradiction with other accepted facts about string theory. We list some of these issues in the following.
Since the full non-perturbative M-theory-completion of string theory is thought to involve not D-branes coupled to the B-field/RR-fields], but their lift (through the duality between type IIA string theory and M-theory) to M-branes coupled to the C-field, what is arguably missing (BDHKMMS 01, Sec. 4.6.5) is an M-brane/C-field charge/flux quantization law, which would reduce to something close to K-theoretic charge quantization in the appropriate limit. See the last item below.
Checking Sen’s conjecture
While the proposal of Witten 98, Section 3 to explain the K-theory charge quantization conjecture via Sen's conjecture on tachyon condensation for open superstrings stretched between D-brane/anti D-brane pairs has become widely accepted folklore, the closest available towards an actual check of this argument via open superstring tachyon condensation seems to be Erler 13 which, however, concludes (on p. 32) with:
It would also be interesting to see if these developments can shed light on the long-speculated relation between string field theory and the K-theoretic description of D-brane charge 75, 76, 77. We leave these questions for future work.
See also Erler 19 which still lists this (on p. 112) among open problems of string field theory:
Are there topological invariants of the open string star algebra representing D-brane charges?
Incompatibility with S-duality
Taken at face value, the K-theory conjecture applied to type IIB string theory breaks the expected S-duality symmetry of the theory: Under this duality the B-field -flux form and the RR-field 3-flux appear on the same footing and in particular mix as linear combinations (jointly coupling to (p,q)-strings), while in twisted K-theory is part of the twist, while is part of what is being twisted, with no evident way to mix these two concepts.
(see also Evslin 06, Sec. 8.3)
Spurious fractional D-brane charges
An old argument of BDHKMMS 01, Sec. 4.5.2 says that equivariant K-theory by itself produces spurious fractional D-brane charges that need to be eliminated by some modification of the K-theory conjecture.
Evidence that this correction is provided by lifting to equivariant stable Cohomotopy instead (Hypothesis H) is offered in BSS 20.
Spurious D-brane charges on group manifolds
Similarly, the analysis of boundary conformal field theory describing open strings on Lie groups (WZW models) does not seem to always agree with the conjectured K-theory classification of the corresponding D-branes:
It might surprise that despite all the progress that has been made in understanding branes on group manifolds, there are usually not enough D-branes known to explain the whole charge group predicted by (twisted) K-theory.
Lift to M-theory
Finally, the lift of the putative D-brane charge quantization in string theory to an M-brane charge quantization in M-theory has remained largely open and problematic, as maybe first highlighted in BDHKMMS 01, Sec. 4.6.5 for a variety of reasons.
However, a highly non-trivial check in DMW 00 successfully matched the first non-trivial differential in the Atiyah-Hirzebruch spectral sequence for topological K-theory, applied on the RR-flux component , to a constraint on the C-fied flux obtained from a path integral-argument in D=11 supergravity.
Incidentally, this and related conditions on the C-field derived in DMW 00 from a path integral-argument in D=11 supergravity are all implied also by the Hypothesis H that the C-field, in turn, is charge quantized in twisted Cohomotopy theory (FSS 19).
Unstable K-theory?
In view of potential lifts to M-theory discussed above, it is noteworthy that the double dimensional reduction of supergravity C-field flux to RR-field flux (under the supposed duality between M-theory and type IIA string theory) does not at face value produce the high-degree RR-flux forms and their low-degree Hodge duals – notably the RR 10-form and its dual 0-form (related to exotic D8-branes and D(-2)-branes) do not appear (recalled in Sati & Schreiber 2024, Ex. 2.13; they are supposed to appear only in massive type IIA string theory, whose relation to flux quantization and M-theory is at best subtle).
But without these forms to complete the potential image of a Chern character map for KU-theory on 10-dimensional manifolds, the usual motivation for flux quantization in K-theory breaks down.
What could still work in this case is flux quantization in some unstable nonabelian cohomology theory (for exposition see geometry of physics – flux quantization), such as unstable K-theory, where the degree of Chern forms is bounded above.
There are some further hints that make this plausible:
As mentioned above, Sen's conjecture motivates the equivalence relation that suggests classifying the Chan-Paton bundles of D-brane-antibrane systems in topological K-theory. In particular, the rank of such bundles is not restricted, which is argued to be required by the schematic construction of lower-dimensional D-branes as bound states of D9 brane-antibrane systems in IIB.
But in Hořava 1998, a similar construction is proposed for IIA using the unstable D9 branes. As before, it is argued there that in order to be able to construct (by using the same -fold construction) any number of lower-dimensional branes, one should be able to add an arbitrary number of D9 branes, thus requiring stabilization in the sense of Whitehead-generalized cohomology theory. However, in Section 4 therein, it is then argued that if one only concentrates on obtaining D0-branes from unstable D9-branes, then for that particular construction sixteen unstable D9-branes, i.e. -bundles, are sufficient to describe any number of D0-branes. The limit is argued to connect to Matrix theory, so that at least in this situation unstable K-theory may be a valid flux/charge quantization law.
Properties
Holographic relation to topological phases of matter
Under AdS/CFT duality in solid state physics the K-theory classification of topological phases of matter corresponds to the K-theory classification of D-brane charge (Ryu-Takayanagi 10a, Ryu-Takayanagi 10v).
Related concepts
References
D-brane charge quantization in topological K-theory
On the conjectural D-brane charge quantization in topological K-theory:
Origin and basics
The idea that D-branes have Dirac charge quantization in topological K-theory originates with the observation that their charge expressed in RR-field flux densities resembles the image of a Chern character:
-
Michael Green, Jeffrey A. Harvey, Gregory Moore, I-Brane Inflow and Anomalous Couplings on D-Branes, Class. Quant. Grav. 14 (1997) 47-52 [doi:10.1088/0264-9381/14/1/008, arXiv:hep-th/9605033]
-
Ruben Minasian, Gregory Moore, K-theory and Ramond-Ramond charge, JHEP 9711:002 (1997) [doi:10.1088/1126-6708/1997/11/002, arXiv:hep-th/9710230]
Further early discussion:
-
Edward Witten, D-Branes And K-Theory, JHEP 9812:019 (1998) [arXiv:hep-th/9810188, doi:10.1088/1126-6708/1998/12/019]
-
Petr Hořava, Type IIA D-Branes, K-Theory, and Matrix Theory (1998). (hep-th/9812135).
-
Daniel Freed, Michael Hopkins, On Ramond-Ramond fields and K-theory, JHEP 0005 (2000) 044 [doi:10.1088/1126-6708/2000/05/044, arXiv:hep-th/0002027]
and with emphasis on the full picture of twisted differential K-theory in:
- Daniel Freed, Dirac charge quantization and generalized differential cohomology, Surveys in Differential Geometry, Int. Press, Somerville, MA, 2000, pp. 129–194 (arXiv:hep-th/0011220, doi:10.4310/SDG.2002.v7.n1.a6, spire:537392)
Here:
- Green, Harvey & Moore (1997), Minasian & Moore (1997) observe that RR-field flux form-expressions for D-brane charge look like images of K-theory classes under the Chern character;

- Witten 98, Section 3 adds the observation that the tachyon condensation – which is expected (this is Sen's conjecture from Sen 98) for open strings between D-brane/anti-D-branes – plausibly implements on their Chan-Paton vector bundles the defining equivalence relation (here) of topological K-theory.
Expression of these D-brane K-theory classes via the Atiyah-Hirzebruch spectral sequence:
-
Juan Maldacena, Gregory Moore, Nathan Seiberg, D-Brane Instantons and K-Theory Charges, JHEP 0111:062,2001 (arXiv:hep-th/0108100)
-
Jarah Evslin, Hisham Sati, Can D-Branes Wrap Nonrepresentable Cycles?, JHEP0610:050,2006 (arXiv:hep-th/0607045)
Specifically for D-branes in WZW models see
- Peter Bouwknegt, A note on equality of algebraic and geometric D-brane charges in WZW models (pdf)
Understanding the solitonic (non-singular) D-branes and their T-duality in K-theory:
- Oren Bergman, Eric G. Gimon, Petr Hořava, Brane Transfer Operations and T-Duality of Non-BPS States, JHEP 9904 (1999) 010 [doi:10.1088/1126-6708/1999/04/010, arXiv:hep-th/9902160]
Towards a matrix model taking these K-theoretic effects into account (K-matrix model):
- Tsuguhiko Asakawa, Shigeki Sugimoto, Seiji Terashima, D-branes, Matrix Theory and K-homology, JHEP 0203 (2002) 034 [doi:10.1088/1126-6708/2002/03/034, arXiv:hep-th/0108085]
Twisted, equivariant and differential refinement
Discussion of charge quantization in twisted K-theory for the case of non-vanishing B-field:
-
Witten 98, Sec. 5.3 (for torsion twists)
-
Peter Bouwknegt, Varghese Mathai, D-branes, B-fields and twisted K-theory, Int. J. Mod. Phys. A 16 (2001) 693-706 [doi:10.1088/1126-6708/2000/03/007, arXiv:hep-th/0002023]
An elaborate proposal for the correct flavour of equivariant KR-theory needed for orientifolds is sketched in:
- Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)
- Saghar S. Hosseini, Yuji Tachikawa, Hao Y. Zhang: Type I anomaly cancellation revisited [arXiv:2505.07933]
Discussion of full-blown twisted differential K-theory and its relation to D-brane charge in type II string theory
- Daniel Grady, Hisham Sati, Ramond-Ramond fields and twisted differential K-theory, Advances in Theoretical and Mathematical Physics 26 5 (2022) [doi:10.4310/ATMP.2022.v26.n5.a2, arXiv:1903.08843]
Discussion of full-blown twisted differential orthogonal K-theory and its relation to D-brane charge in type I string theory (on orientifolds):
- Daniel Grady, Hisham Sati, Twisted differential KO-theory (arXiv:1905.09085)
Reviews
-
Kasper Olsen, Richard Szabo, Brane Descent Relations in K-theory, Nucl.Phys. B566 (2000) 562-598 (arXiv:hep-th/9904153)
-
Kasper Olsen, Richard Szabo, Constructing D-Branes from K-Theory, Adv. Theor. Math. Phys. 3 (1999) 889-1025 (arXiv:hep-th/9907140)
-
John Schwarz, TASI Lectures on Non-BPS D-Brane Systems (arXiv:hep-th/9908144)
-
Edward Witten, Overview Of K-Theory Applied To Strings, Int. J. Mod. Phys. A16:693-706, 2001 (arXiv:hep-th/0007175)
-
Greg Moore, K-Theory from a physical perspective, in: Ulrike Tillmann (ed.) Topology, Geometry and Quantum Field Theory, Proceedings of the 2002 Oxford Symposium in Honour of the 60th Birthday of Graeme Segal, Cambridge University Press (2004) (arXiv:hep-th/0304018, doi:10.1017/CBO9780511526398.011)
-
Juan José Manjarín, Topics on D-brane charges with B-fields, Int. J. Geom. Meth. Mod. Phys. 1 (2004) (arXiv:hep-th/0405074)
-
Jarah Evslin, What Does(n’t) K-theory Classify?, Modave Summer School in Mathematical Physics (arXiv:hep-th/0610328, spire:730502)
-
Stefan Fredenhagen, Physical Background to the K-Theory Classification of D-Branes: Introduction and References (doi:10.1007/978-3-540-74956-1_1), chapter in: Dale Husemoeller, Michael Joachim, Branislav Jurčo, Martin Schottenloher, Basic Bundle Theory and K-Cohomology Invariants, Lecture Notes in Physics, Springer (2008) 1-9 [doi:10.1007/978-3-540-74956-1, pdf]
-
Fabio Ruffino, Topics on topology and superstring theory (arXiv:0910.4524)
-
Hisham Sati, Urs Schreiber: Flux Quantization, in Encyclopedia of Mathematical Physics 2nd ed, Elsevier (2024) [arXiv:2402.18473]
Amplification of torsion-charges implied by charge quantization in Ktheory
-
Volker Braun: K-Theory Torsion [arXiv:hep-th/0005103]
-
Ilka Brunner, Jacques Distler, Torsion D-Branes in Nongeometrical Phases, Adv. Theor. Math. Phys. 5 (2002) 265-309 [doi:10.4310/ATMP.2001.v5.n2.a3, arXiv:hep-th/0102018]
-
Ilka Brunner, Jacques Distler, Rahul Mahajan, Return of the Torsion D-Branes, Adv. Theor. Math. Phys. 5 (2002) 311-352 [doi:10.4310/ATMP.2001.v5.n2.a4, arXiv:hep-th/0106262]
Review of D-branes charge seen in KK-theory:
- Richard Szabo, D-branes and bivariant K-theory, Noncommutative Geometry and Physics 3 1 (2013): 131. (arXiv:0809.3029)
based on
-
Rui Reis, Richard Szabo, Geometric K-Homology of Flat D-Branes , Commun. Math. Phys. 266 (2006) 71-122 [arXiv:hep-th/0507043]
-
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-Branes, RR-Fields and Duality on Noncommutative Manifolds, Commun. Math. Phys. 277 (2008) 643-706 [doi:10.1007/s00220-007-0396-y, arXiv:hep-th/0607020]
-
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, Noncommutative correspondences, duality and D-branes in bivariant K-theory, Adv. Theor. Math. Phys. 13:497-552, 2009 (arXiv:0708.2648)
-
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-branes, KK-theory and duality on noncommutative spaces, J. Phys. Conf. Ser. 103 012004 (2008) [doi:10.1088/1742-6596/103/1/012004, arXiv:0709.2128]
In particular (BMRS2) discusses the definition and construction of D-brane charge as a generalized index in KK-theory. The discussion there focuses on the untwisted case. Comments on the generalization of this to topologicall non-trivial B-field and hence twisted K-theory is in
- Richard Szabo, D-Branes, Tachyons and K-Homology, Mod. Phys. Lett. A17 (2002) 2297-2316 (arXiv:hep-th/0209210)
Conceptual problems
But there remain conceptual issues with the proposal that D-brane charge is in K-theory, as highlighted in
-
Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, section 4.5.2 and 4.6.5 of Triples, Fluxes, and Strings, Adv. Theor. Math. Phys. 4 (2002) 995-1186 [arXiv:hep-th/0103170, pdf]
-
Jarah Evslin, section 8 of: What Does(n’t) K-theory Classify?, Second Modave Summer School in Mathematical Physics [arXiv:hep-th/0610328]
In particular, actual checks of the proposal that D-brane charge is given by K-theory, via concrete computation in boundary conformal field theory, have revealed some subtleties:
-
Stefan Fredenhagen, Thomas Quella, Generalised permutation branes, JHEP 0511:004 (2005) [arXiv:hep-th/0509153, doi:10.1088/1126-6708/2005/11/004]
It might surprise that despite all the progress that has been made in understanding branes on group manifolds, there are usually not enough D-branes known to explain the whole charge group predicted by (twisted) K-theory. […] it is fair to say that a satisfactory answer is still missing.
The closest available towards an actual check of the argument for K-theory via open superstring tachyon condensation (Witten 98, Section 3) seems to be
- Theodore Erler, Analytic Solution for Tachyon Condensation in Berkovits’ Open Superstring Field Theory, JHEP 1311 (2013) 007 [doi:10.1007/JHEP11(2013)007, arXiv:1308.4400]
which, however, concludes (on p. 32) with:
It would also be interesting to see if these developments can shed light on the long-speculated relation between string field theory and the K-theoretic description of D-brane charge 75, 76, 77]. We leave these questions for future work.
See also
- Theodore Erler, Four Lectures on Analytic Solutions in Open String Field Theory (arXiv:1912.00521, spire:1768105)
which still lists (on p. 112) among open problems of string field theory:
“Are there topological invariants of the open string star algebra representing D-brane charges?”
For orbifolds in equivariant K-theory
The proposal that D-brane charge on orbifolds is measured in equivariant K-theory (orbifold K-theory) goes back to
It was pointed out that only a subgroup of equivariant K-theory can be physically relevant in
- Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, around (137) of: Triples, Fluxes, and Strings, Adv.Theor.Math.Phys. 4 (2002) 995-1186 (arXiv:hep-th/0103170)
Further discussion of equivariant K-theory for D-branes on orbifolds includes the following:
-
Hugo García-Compeán, D-branes in orbifold singularities and equivariant K-theory, Nucl.Phys. B557 (1999) 480-504 (arXiv:hep-th/9812226)
-
Matthias Gaberdiel, Bogdan Stefanski, Dirichlet Branes on Orbifolds, Nucl.Phys.B578:58-84, 2000 (arXiv:hep-th/9910109)
-
Igor Kriz, Leopoldo A. Pando Zayas, Norma Quiroz, Comments on D-branes on Orbifolds and K-theory, Int. J. Mod. Phys. A 23 (2008) 933-974 [arXiv:hep-th/0703122]
-
Richard Szabo, Alessandro Valentino, Ramond-Ramond Fields, Fractional Branes and Orbifold Differential K-Theory, Commun.Math.Phys.294:647-702, 2010 (arXiv:0710.2773)
Discussion of real K-theory for D-branes on orientifolds includes the following:
The original observation that D-brane charge for orientifolds should be in KR-theory is due to
and was then re-amplified in
-
Sergei Gukov, K-Theory, Reality, and Orientifolds, Commun.Math.Phys. 210 (2000) 621-639 (arXiv:hep-th/9901042)
-
Oren Bergman, E. Gimon, Shigeki Sugimoto, Orientifolds, RR Torsion, and K-theory, JHEP 0105:047, 2001 (arXiv:hep-th/0103183)
With further developments in
- Varghese Mathai, Michael Murray, Daniel Stevenson, Type I D-branes in an H-flux and twisted KO-theory, JHEP 0311 (2003) 053 (arXiv:hep-th/0310164)
Discussion of orbi-orienti-folds using equivariant KO-theory is in
-
N. Quiroz, Bogdan Stefanski, Dirichlet Branes on Orientifolds, Phys.Rev. D66 (2002) 026002 (arXiv:hep-th/0110041)
-
Volker Braun, Bogdan Stefanski, Orientifolds and K-theory (arXiv:hep-th/0206158)
-
H. Garcia-Compean, W. Herrera-Suarez, B. A. Itza-Ortiz, O. Loaiza-Brito, D-Branes in Orientifolds and Orbifolds and Kasparov KK-Theory, JHEP 0812:007, 2008 (arXiv:0809.4238)
Discussion of the alleged K-theory classification of D-brane charge in relation to the M-theory C-field is in
- Duiliu-Emanuel Diaconescu, Gregory Moore, Edward Witten, Gauge Theory, and a Derivation of K-Theory from M-Theory, Adv.Theor.Math.Phys.6:1031-1134,2003 (arXiv:hep-th/0005090), summarised in A Derivation of K-Theory from M-Theory (arXiv:hep-th/0005091)
See also
- Inaki Garcia-Etxebarria, Angel Uranga, From F/M-theory to K-theory and back, JHEP 0602:008,2006 (arXiv:hep-th/0510073)
More complete discussion of double dimensional reduction of the supergravity C-field in 11d to the expected B-field and RR-field flux forms in 10d:
-
Varghese Mathai, Hisham Sati, Some Relations between Twisted K-theory and Gauge Theory, JHEP0403:016,2004 (arXiv:hep-th/0312033)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory and type IIA string theory, Journal of Geometry and Physics, Volume 114, Pages 91-108 April 2017 (arXiv:1606.03206, doi:10.1016/j.geomphys.2016.11.024)
Last revised on May 26, 2024 at 07:02:11. See the history of this page for a list of all contributions to it.