nLab M-brane 3-algebra
Context
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
In the construction of the Lagrangian density for the supersymmetric worldvolume gauge quantum field theory on coincident M2-branes (the BLG model/ABJM model, a conformal super-Chern-Simons theory coupled to matter-fields) a certain algebraic structure appears – and at least in the BLG model it appears at a pivotal stage in the proof of supersymmetry – which is given by a trilinear map on an inner product space
that is subject to some axioms which are different from but clearly reminiscent to the axioms on the Lie bracket of a Lie algebra, (which is of course a bilinear map).
In special cases, but not generally, this algebraic structure is a special case of a structure introduced by Filippov, which could be called a Filippov algebra, but which mostly came to alternatively be called a 3-Lie algebra or a Lie 3-algebra or often just a 3-algebra.
Unfortunately, in homotopy theory and higher algebra, these terms refer to something different, namely to L-infinity algebras or categorifications of associative algebras to n-algebras – but the structure seen in the BLG model on M2-branes is none of these.
Hence to be on the safe side, one may want to speak of M2-brane 3-algebras or maybe M-brane algebras, for definiteness
Moreover, while this “M2-brane 3-algebra” appeared to be a central ingredient in the BLG model, it makes no appearance in the ABJM model, which however generalizes and hence subsumes the BLG model, up to slight re-identifications of terms.
Indeed, inspection reveals that “M2-brane 3-algebras” give rise to and may be re-constructed from data in ordinary Lie theory, namely from pairs consisting of a metric Lie algebra and a dualizable Lie algebra representation.
This is due to dMFFMER 08, Theorem 11, recalled as Prop. below.
(…)
Definition
Definition
An M2-brane 3-algebra is
-
a metric on , hence a non-degenerate inner product space (not required to be positive definite);
-
a trilinear function, the 3-bracket
such that the following three axioms hold, for all elements :
-
(unitarity)
-
(symmetry)
-
(fundamental identity)
In this generality, and under the name “generalized metric Lie 3-algebras”, this is due to Cherkis-Saemann 08, 41, see dMFFMER 08, Def. 1
Properties
Equivalence to metric Lie representations
For the following, let the ground field be the real numbers and take all vector spaces involved to be real and finite-dimensional.
For definiteness, we make the following explicit:
Definition
An orthogonal representation of a metric Lie algebra is
-
a metric vector space
hence a non-degenerate real inner product space;
of on .
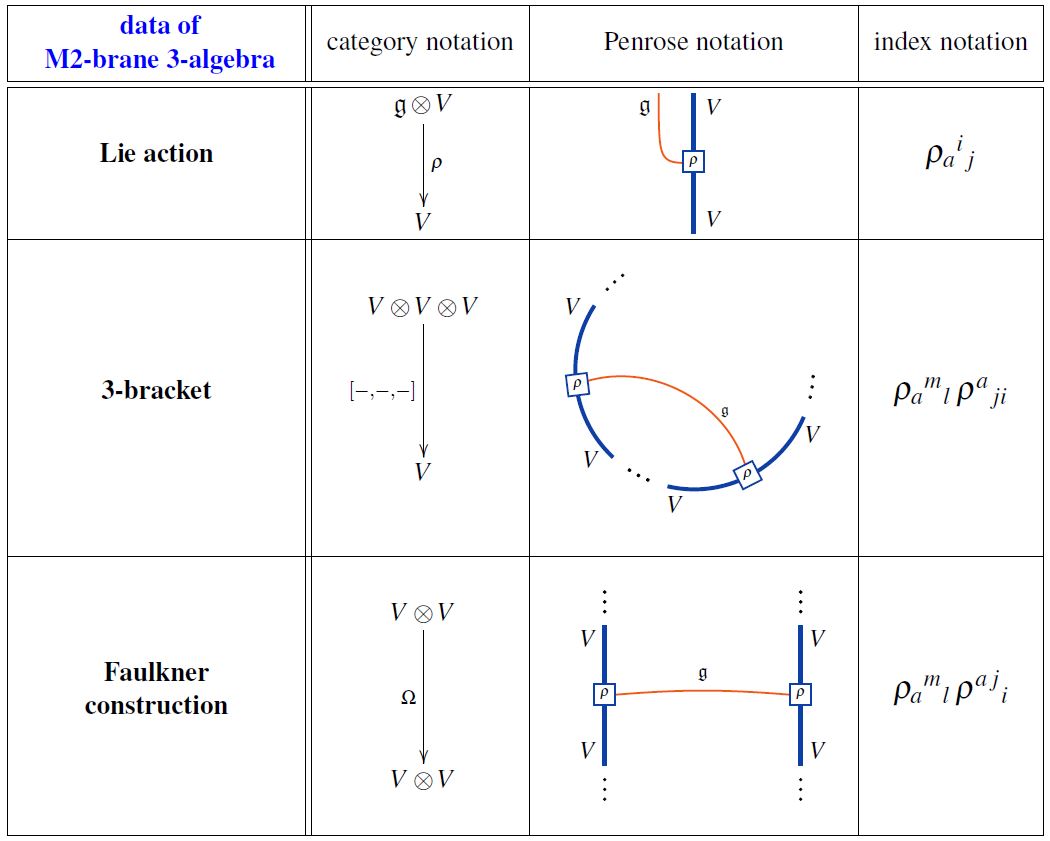
Remark
(linear duals and adjuncts/transposition)
Given an orthogonal representation of a metric Lie algebra as in Def. , the non-degenerate inner products on and on exhibit these as self-dual objects in the monoidal category of finite-dimensional vector spaces (with respect to the tensor product of vector spaces).
This means that by passsing to adjuncts we may regard linear maps of the form
equivalently as linear maps of the form
where is the dual vector space; and similarly for .
Once we choose a linear basis of , with respect to which the metric tensor has components
this forming of adjuncts is equivalently the yoga of “raising and lowering of indices via the metric”. Similarly for a choice of linear basis for the Lie algebra, and the induced components
Specifically, given the basis component of the Lie action , defined by
we get the components of the adjunct
by contracting the original component (3) with the components (1) (2) of the metric tensors:
Definition
(trilinear map induced from metric Lie representation – Faulkner construction)
Given an orthogonal representation of a metric Lie algebra as in Def. , define
-
given by
(6) -
(7)
hence
In this form and with this notation this is dMFFMER 08, equation (9) and over Prop. 10 (except that we write “” for their “”). The construction itself, up to one dualization of , was introduced in Faulkner 73.
Remark
(component expression of trilinear bracket)
After a choice of linear bases as in Remark , in terms of which Lie algebra elements are expanded as and representation vectors are expanded as , the defining equation (6)
reads
(where here and in the following we use the Einstein summation convention), hence reads
hence equivalently reads
hence says that the tensor is equal to the adjunct (4) of the Lie action tensor , given in components by the evident “raising and lowering of indices via the metrics” as in (5):
With this, the induced trilinear bracket (7)
is given in components as
Proposition
(M2-brane 3-algebras are equivalent to metric Lie representations)
Given an orthogonal representation of a metric Lie algebra as in Def. , its induced trilinear map (Def. ) satisfies the axioms of an M2-brane 3-algebra (Def. ).
Hence this assignment defines a function from isomorphism classes of orthogonal representations of metric Lie algebras to isomorphism classes of M2-brane 3-algebras
Moreover, restricted to faithful representations, this function is a bijection:
This is dMFFMER 08, Prop. 10 and Theorem 11.
Relation to Lie algebra weight systems on chord diagrams
In Penrose notation (string diagram-notation), the trilinear bracket induced by a metric Lie representation according to Def. looks as follows:
With Prop. this shows that M2-brane 3-algebras are equivalently the datum that Lie algebra weight systems on (horizontal) chord diagrams assign to a single chord.
from Sati-Schreiber 19c
References
Appearance in M2-brane theory
The idea that some higher-arity version of the Lie bracket may be relevant for M2-M5 brane intersections originates with attempts of generalizing Nahm's equations for fuzzy funnels of D2-D4 brane intersections in
- Anirban Basu, Jeffrey Harvey, The M2-M5 Brane System and a Generalized Nahm’s Equation, Nucl.Phys. B713 (2005) 136-150 (arXiv:hep-th/0412310)
Motivated by this, the M2-brane 3-algebra appears in the construction of the BLG model for the worldvolume quantum field theory on 2 coincident M2-branes in
-
Jonathan Bagger, Neil Lambert, Modeling Multiple M2’s, Phys. Rev. D75, 045020 (2007). (hep-th/0611108)
-
Jonathan Bagger, Neil Lambert, Gauge Symmetry and Supersymmetry of Multiple M2-Branes, Phys. Rev. D77, 065008 (2008). (arXiv:0711.0955)
further highlighted as such in
- Andreas Gustavsson, Algebraic structures on parallel M2-branes Nucl. Phys. B811, 66-76 (2009) (arXiv:0709.1260)
(whence the “BLG” of the BLG model)
and further explored in
- Paul de Medeiros, José Figueroa-O'Farrill, Elena Méndez-Escobar, Metric Lie 3-algebras in Bagger-Lambert theory, JHEP 0808 : 045, 2008 (arXiv:0806.3242)
From here on a myriad of references followed up. Review includes:
(…)
Equivalence to metric Lie representations
The full generalized axioms on the M2-brane 3-algebra and first insights into their relation to Lie algebra representations of metric Lie algebras is due to
- Sergey Cherkis, Christian Saemann, Section 4 of: Multiple M2-branes and Generalized 3-Lie algebras, Phys. Rev. D78:066019, 2008 (arXiv:0807.0808)
The full identification of M2-brane 3-algebras with dualizable Lie algebra representations over metric Lie algebras is due to
- Paul de Medeiros, José Figueroa-O'Farrill, Elena Méndez-Escobar, Patricia Ritter, On the Lie-algebraic origin of metric 3-algebras, Commun. Math. Phys. 290:871-902, 2009 (arXiv:0809.1086)
reviewed in
- José Figueroa-O'Farrill, slide 145 onwards in: Triple systems and Lie superalgebras in M2-branes, ADE and Lie superalgebras, talk at IPMU 2009 (pdf, pdf)
further explored in
- José Figueroa-O'Farrill, Simplicity in the Faulkner construction, Journal of Physics A: Mathematical and Theoretical, Volume 42, Number 44 (arXiv:0905.4900)
and putting to use the Faulkner construction that was previously introduced in
- John Faulkner, On the geometry of inner ideals, Journal of Algebra, Volume 26, Issue 1, July 1973, Pages 1-9 (doi:10.1016/0021-8693(73)90032-X)
See also:
-
Sam Palmer, Christian Saemann, section 2 of M-brane Models from Non-Abelian Gerbes, JHEP 1207:010, 2012 (arXiv:1203.5757)
-
Patricia Ritter, Christian Saemann, section 2.5 of Lie 2-algebra models, JHEP 04 (2014) 066 (arXiv:1308.4892)
-
Christian Saemann, appendix A of Lectures on Higher Structures in M-Theory (arXiv:1609.09815)
and
- Jakob Palmkvist, Three-algebras, triple systems and 3-graded Lie superalgebras, J. Phys. A43:015205, 2010 (arXiv:0905.2468)
Last revised on May 25, 2020 at 09:32:32. See the history of this page for a list of all contributions to it.