nLab Solovay-Kitaev theorem

Idea

Given a finitely generated and dense subgroup $\langle g_1, g_1^{-1} \cdots, g_n, g_n^{-1} \rangle$ of the topological group SU(2), the Solovay-Kitaev theorem [Kitaev (1997), Nielsen & Chuang (2000, §A3)] gives a strong bound on the length of sequences of elements from $\{g_1, \cdots, g_n\}$ which are needed in order to approximate any given element $g \,\in\, SU(2)$ to given accuracy.

In quantum computation-theory one interprets:

1. the set $\{g_0, \cdots, g_n\}$ as a given set of (operations of) quantum gates on qbits

   (that the subgroup these generate is dense in SU(2) is said to mean that this is a universal set of quantum gates);

2. the target element $g \,\in\, SU(2)$ as an intended operation on qbits (an intended quantum program);

3. the sequence of elements $g_i$ used to approximate $g$ as a quantum circuit realizing the quantum program (“quantum compilation”),

and then the Solovay-Kitaev theorem guarantees that the maximum depth of the quantum circuit grows only slowly with its required accuracy.

In fact, the theorem holds in the generality of $SU(d)$, $d \in \mathbb{N}_{\geq 1}$, which in terms of quantum computation corresponds to working with qdits instead of just qbits.

Regarding the practical relevance, it has been argued [MO:a/22197] that quantum computing-hardware such as based on superconductors will already allow to approximate any operation on a “physical qbit” by a single quantum gate, but that for such hardware the Solovay-Kitaev theorem is still relevant on the level of “logical qbits”, i.e. taking quantum error correction into account.

Similarly, in topological quantum computation the available set of basic anyon braid gates is typically far from the usual QBit-basis requiring substantial effort in “topological quantum compilation” (e.g. Bonesteel, Hormozi, Zikos & Simon (2005), Hormozi, Zikos, Bonesteel & Simon (2007), Hormozi, Bonesteel & Simon (2009)).

For example, the following lengthy braid has been proposed [Hormozi, Zikos, Bonesteel & Simon (2007)] as a possible topological quantum compilation of a single CNOT gate:

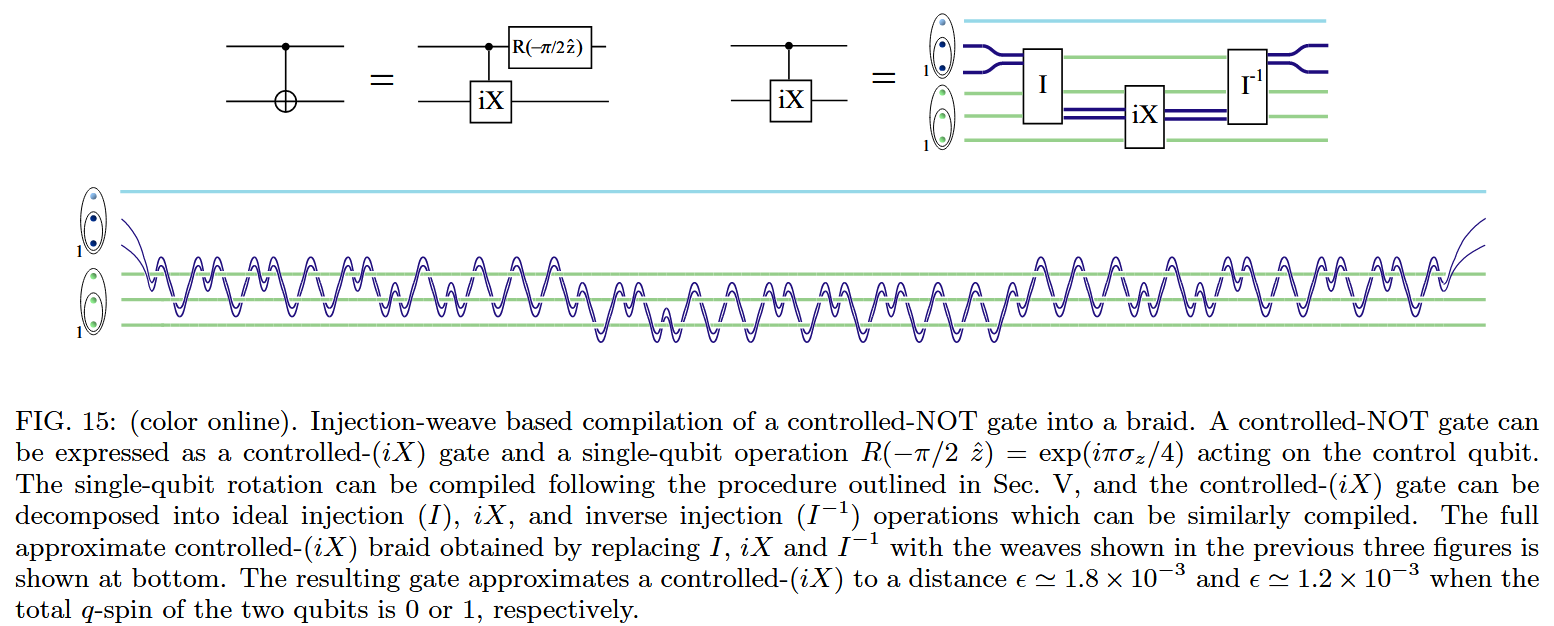
References

General

According to Dawson & Nielsen (2006, p. 13) the first announcement of the theorem was

• “by Solovay in 1995 on an email discussion list”.

A proof was then outlined in:

• Alexei Kitaev, Thm. 4.8 of: Quantum computations: algorithms and error correction, Russian Mathematical Surveys, 52 6 (1997) [doi:10.1070/RM1997v052n06ABEH002155, pdf]

followed by talk announcement:

• Robert Solovay, Lie Groups and Quantum Circuits, talk at MSRI (2000) [webpage, mp4]

Following Kitaev (1997), a full proof was spelled out in:

• Michael A. Nielsen, Isaac L. Chuang, Solovay-Kitaev theorem, Appendix 3 of: Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]

Review:

• Alexei Kitaev, A. H. Shen, M. N. Vyalyi, §8.3 in: Classical and Quantum Computation, Graduate Studies in Mathematics 47, Amer. Math. Soc. (2002) [doi:10.1090/gsm/047]

• Christopher M. Dawson, Michael A. Nielsen, The Solovay-Kitaev algorithm, Quantum Information & Computation 6 1 (2006) 81–95 [arXiv:quant-ph/0505030, doi:10.5555/2011679.2011685]

See also:

• Wikipedia, Solovay-Kitaev theorem

• Maris Ozols, The Solovay-Kitaev theorem [pdf]

Further refinement of the algorithm:

• Attila B. Nagy, On an implementation of the Solovay-Kitaev algorithm, 10th Rhine Workshop on Computer Algebra [arXiv:quant-ph/0606077]

Quantum circuit compilation

More on quantum circuit compilation:

• Neil J. Ross, Chapters 6-7 in: Algebraic and Logical Methods in Quantum Computation, Ph.D. thesis, Dalhousie University (2015) [arXiv:1510.02198]

• Adi Botea, Akihiro Kishimoto, Radu Marinescu, On the Complexity of Quantum Circuit Compilation, Proceedings of the International Symposium on Combinatorial Search, 9 1 (2018) [doi:10.1609/socs.v9i1.18463]

• Robert Wille; Stefan Hillmich; Lukas Burgholzer, Efficient and Correct Compilation of Quantum Circuits, in 2020 IEEE International Symposium on Circuits and Systems (ISCAS) IEEE Explore (2020) [doi:10.1109/ISCAS45731.2020.9180791]

• Nathanial Stemen, Quantum Circuit Compilation from the Ground Up (2022) [pdf]

• Giulia Meuli, Fereshte Mozafari, Bruno Schmitt, Heinz Riener, Mathias Soeken, Giovanni De Micheli: Quantum Compilation

A textbook account:

• Marco Maronese, Lorenzo Moro, Lorenzo Rocutto, Enrico Prati, Quantum Compiling, in Quantum Computing Environments, Springer (2021) 39-74 [arXiv:2112.00187, doi:10.1007/978-3-030-89746-8_2]

Quantum compilation with a proof assistant based on QWIRE:

• Kesha Hietala, Robert Rand, Shih-Han Hung, Xiaodi Wu, Michael Hicks, A verified optimizer for Quantum circuits, Proceedings of the ACM on Programming Languages 5 Issue POPL 37 (2021) 1–29 [doi:10.1145/3434318]

• Kesha Hietala, Robert Rand, Shih-Han Hung, Liyi Li, Michael Hicks, Proving Quantum Programs Correct, in 12th International Conference on Interactive Theorem Proving (ITP 2021), Leibniz International Proceedings in Informatics (LIPIcs) 193 (2021) [arXiv:2010.01240]

• Kesha Hietala, A verified software toolchain for quantum programming (2022) [pdf]

Topological quantum compilation

Discussion of the Solovay-Kitaev theorem for quantum compilation in the context of topological quantum computation:

• Nicholas E. Bonesteel, Layla Hormozi, Georgios Zikos, Steven H. Simon, Braid Topologies for Quantum Computation, Phys. Rev. Lett. 95 140503 (2005) [arXiv:quant-ph/0505065, doi:10.1103/PhysRevLett.95.140503]

• Layla Hormozi, Georgios Zikos, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Compiling, Phys. Rev. B 75 165310 (2007) [arXiv:quant-ph/0610111, doi:10.1103/PhysRevB.75.165310]

• Layla Hormozi, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Computing with Read-Rezayi States, Phys. Rev. Lett. 103 160501 (2009) [doi:10.1103/PhysRevLett.103.160501, arXiv:0903.2239]

• Joren W. Brunekreef, Topological Quantum Computation and Quantum Compilation, Utrecht (2014) [studenttheses.uu.nl:20.500.12932/17738]

• Keisuke Fujii, Quantum Computation with Topological Codes: from qubit to topological fault-tolerance, SpringerBriefs in Mathematical Physics 8 (2015) [arXiv:1504.01444, doi:10.1007/978-981-287-996-7]

• Vadym Kliuchnikov, Alex Bocharov, Krysta M. Svore, Asymptotically Optimal Topological Quantum Compiling, Phys. Rev. Lett. 112 (2014) 140504 [arXiv:1310.4150, doi:10.1103/PhysRevLett.112.140504]

• Caitlin Carnahan, Daniel Zeuch, Nicholas E. Bonesteel, Systematically generated two-qubit anyon braids, Phys. Rev. A 93 052328 (2016) [arXiv:1511.00719, doi:10.1103/PhysRevA.93.052328]

• Emil Génetay-Johansen, Tapio Simula, Section IV of: Fibonacci anyons versus Majorana fermions – A Monte Carlo Approach to the Compilation of Braid Circuits in $SU(2)_k$ Anyon Models, PRX Quantum 2 010334 (2021) [arXiv:2008.10790, doi:10.1103/PRXQuantum.2.010334]