nLab quantum error correction

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Redirected from "logical qbits".
Contents

Context

Quantum systems

quantum logic


quantum physics


quantum probability theory – observables and states


quantum information


quantum computation

qbit

quantum algorithms:


quantum sensing


quantum communication

Computation

constructive mathematics, realizability, computability

intuitionistic mathematics

propositions as types, proofs as programs, computational trinitarianism

Constructive mathematics

Realizability

Computability

Contents

Idea

General

Quantum error correction is concerned with ensuring the robustness of quantum computation against noise (as in classical error correction) and particularly against quantum noise and quantum decoherence (e.g. against bit flip errors).

From Ferris & Poulin 2013:

The basic principle of quantum error correction (QEC) is to encode information into the long-range correlations of entangled quantum many-body states in such a way that it cannot be accessed locally. When a local error affects the system, it leaves a detectable imprint—called the error syndrome. The decoding problem consists in inferring the recovery with greatest probability of success given the error syndrome. In general, this is a hard problem, but for well-chosen codes, it can be solved efficiently either exactly or heuristically.

From Steane 06:

Error correction is especially important in quantum computers, because efficient quantum algorithms make use of large scale quantum interference, which is fragile, i.e. sensitive to imprecision in the computer and to unwanted coupling between the computer and the rest of the world. This makes large scale quantum computation so difficult as to be practically impossible unless error correction methods are used. Indeed, before quantum error correction was discovered, it seemed that this fragility would forbid large scale quantum computation. The ability to correct a quantum computer efficiently without disturbing the coherence of the computation is highly non-intuitive, and was thought more or less impossible. The discovery of powerful error correction methods therefore caused much excitement, since it converted large scale quantum computation from a practical impossibility to a possibility.

From Devitt, Nemoto & Munro 2009:

Starting in 1995, several papers appeared, in rapid succession, proposing codes which were appropriate to perform error correction on quantum data (Sho95; Ste96a; CS96; LMPZ96; BSW96). This was a key theoretical development needed to convince the general community that quantum computation was indeed a possibility. Since this initial introduction, the progress in this field has been extensive.

From Zhu & Cross 20:

Although we are currently in an era of quantum computers with tens of noisy qubits, it is likely that a decisive, practical quantum advantage can only be achieved with a scalable, fault-tolerant, error-corrected quantum computer. Therefore, development of quantum error correction is one of the central themes of the next five to ten years.

Lucero 21:

Within the decade, Google aims to build a useful, error-corrected quantum computer. [⋯][\cdots] Our journey to build an error-corrected quantum computer within the decade includes several scientific milestones, including building an error-corrected logical qubit.

Specifically on holographic quantum error correcting codes (see references below):

From Harlow 20:

The codes provided by AdS/CFT often come close to saturating theoretical bounds on the performance of quantum codes. It seems AdS/CFT may be a tool for discovering better quantum cryptography?

WVSB 20:

[[ holographic codes ]] could be promising candidates to circumvent our results and could possibly realise a universal set of unitary implementations of logical operators.

From CDCW 21:

There are a number of reasons to suspect that holographic codes may be of practical use for quantum computing.

Holographic codes can admit erasure thresholds comparable to that of the widely-studied surface code, and likewise for their threshold against Pauli errors. Their holographic structure also naturally leads to an organization of encoded qubits into a hierarchy of levels of protection from errors, which could be useful for applications which call for many qubits withvarying levels of protection. In particular, this is reminiscent of many schemes for magic state distillation – and indeed, the concatenated codes utilized for magic state distillation share a similar hierarchical structure to holographic codes. The layered structure of holographic codes is also reminiscent of memory architectures in classical computers, where it is useful to have different levels of short- and long-term memory. Although these codes have some notable drawbacks, in particular holographic stabilizer codes require nonlocal stabilizer generators, other codes such as concatenated codes suffer similar drawbacks and have still proven to be useful. Conversely, the stringent requirement of non-local stabilizer generators allows holographic codes to protect many more qubits than a topological code and in fact attain a finite nonzero encoding rate, which is typically not possible for topological codes. Nonetheless, many open questions remain about the usefulness of holographic codes for fault-tolerant quantum computing.

Quantum error correcting codes

The simple but important special case of passive correction of erasures may be handled by quantum error correcting codes:

Recall that a classical error correcting code on a finite set of states LL is, typically, a choice of injection of LL into some larger set, typically a Cartesian power

L↪codeP≔H×⋯×H L \overset{code}{\hookrightarrow} P \coloneqq H \times \cdots \times H

(often considered in the form of linear codes, but classical nonetheless). In quantum physics the Cartesian product of sets of states is replaced by the tensor product of Hilbert spaces.

For ℒ\mathcal{L} a given Hilbert space of quantum states (finite-dimensional in practice), a quantum error correcting code is a choice of linear embedding (the code subspace) of ℒ\mathcal{L} into a larger Hilbert spaces, often an nn-fold tensor product of copies of some ℋ\mathcal{H}:

ℒlogicalqbits ↪codesubspacecode 𝒫≔ℋ (1)⊗⋯⊗ℋ (n)physicalqbits, \array{ \underset{ {\color{blue}logical} \atop {\color{blue}qbits} }{ \mathcal{L} } & \underoverset {{\color{blue}code} \atop {\color{blue} subspace}} {\;\;\;code\;\;\;} { \hookrightarrow } & \mathcal{P} \coloneqq \underset{ \color{blue} physical\;qbits }{ \mathcal{H}^{(1)} \otimes \cdots \otimes \mathcal{H}^{(n)} } } \,,

such that the information in code(ψ)code(\psi) in some of the tensor factors ℋ (i)\mathcal{H}^{(i)} can be lost without obstructing the reconstruction of ψ\psi (e.g. Rowell & Wang 17, Sec. 3.2.3).

(Often one demands additional properties, such as that a given set of linear operators OO (quantum observables) acting on ψ∈ℋ\psi \in \mathcal{H} are implemented on code(ψ)code(\psi) by combinations of operators that act non-trivially only on some of the tensor factors.)

While this is superficially analogous to a classical error correcting code, the crucial and subtle difference is that quantum error correction codes thus take place in a non-Cartesian symmetric monoidal category. For this reason, effects of quantum entanglement play a paramount role in quantum error correction codes.

Example

Specific examples

Bit flip codes

See at bit flip code.

A 3-qutrit code

The following is a simple illustrative example from Cleve, Gottesman & Lo 99, p. 1-2:

Consider a quantum system with a 3-dimensional space of quantum states:

ℋ≔ℂ 3=Span(|0⟩,|1⟩,|2⟩) \mathcal{H} \;\coloneqq\; \mathbb{C}^3 \;=\; Span\big( \left\vert 0 \right\rangle,\, \left\vert 1 \right\rangle,\, \left\vert 2 \right\rangle \big)

and consider a code space inside 3 copies of this space given by the following linear map

ℋ ⟶AAAAcodeAAAA ℋ ⊗3 α|0⟩ + β|1⟩ + γ|2⟩ ↦ α13(|000⟩+|111⟩+|222⟩) + β13(|012⟩+|120⟩+|201⟩) + γ13(|021⟩+|102⟩+|210⟩) \array{ \mathcal{H} & \overset{ \phantom{AAAA} code \phantom{AAAA} }{\longrightarrow}& \mathcal{H}^{\otimes 3} \\ \array{ & \alpha \left\vert 0 \right\rangle \\ + & \beta \left\vert 1 \right\rangle \\ + & \gamma \left\vert 2 \right\rangle } & \mapsto & \array{ & \alpha \tfrac{1}{\sqrt{3}} \big( \left\vert 000 \right\rangle + \left\vert 111 \right\rangle + \left\vert 222 \right\rangle \big) \\ + & \beta \tfrac{1}{\sqrt{3}} \big( \left\vert 012 \right\rangle + \left\vert 120 \right\rangle + \left\vert 201 \right\rangle \big) \\ + & \gamma \tfrac{1}{\sqrt{3}} \big( \left\vert 021 \right\rangle + \left\vert 102 \right\rangle + \left\vert 210 \right\rangle \big) } }

This code corrects errors consisting of the loss of one of the three copies, in the following sense:

There is a linear operator acting only on two of the three copies, explicitly given (ADH 14 (3.6)) by

ℋ⊗ℋ ⟶U (12) ℋ⊗ℋ |00⟩ ↦ |00⟩ |01⟩ ↦ |12⟩ |02⟩ ↦ |21⟩ |10⟩ ↦ |22⟩ |11⟩ ↦ |01⟩ |12⟩ ↦ |10⟩ |20⟩ ↦ |11⟩ |21⟩ ↦ |20⟩ |22⟩ ↦ |02⟩ \array{ \mathcal{H} \otimes \mathcal{H} & \overset{ \;\;\;\;\;\; U^{(12)} \;\;\;\;\;\; }{\longrightarrow} & \mathcal{H} \otimes \mathcal{H} \\ \left\vert 00 \right\rangle &\mapsto& \left\vert 00 \right\rangle \\ \left\vert 01 \right\rangle &\mapsto& \left\vert 12 \right\rangle \\ \left\vert 02 \right\rangle &\mapsto& \left\vert 21 \right\rangle \\ \left\vert 10 \right\rangle &\mapsto& \left\vert 22 \right\rangle \\ \left\vert 11 \right\rangle &\mapsto& \left\vert 01 \right\rangle \\ \left\vert 12 \right\rangle &\mapsto& \left\vert 10 \right\rangle \\ \left\vert 20 \right\rangle &\mapsto& \left\vert 11 \right\rangle \\ \left\vert 21 \right\rangle &\mapsto& \left\vert 20 \right\rangle \\ \left\vert 22 \right\rangle &\mapsto& \left\vert 02 \right\rangle }

such that

(U (12)⊗id (3))∘code(|ψ⟩)=|ψ⟩⊗13(|00⟩+|11⟩+|22⟩) \big( U^{(12)} \otimes id^{(3)} \big) \circ code \big( \left\vert \psi \right\rangle \big) \;\; = \;\; \left\vert \psi \right\rangle \, \otimes \, \tfrac{1}{\sqrt{3}} \left( \left\vert 00 \right\rangle + \left\vert 11 \right\rangle + \left\vert 22 \right\rangle \right)

The HaPPY code

The HaPPY code is a quantum error correction code (a class of such codes really, indexed by a “cutoff” natural number) which is thought to exhibit characteristic properties akin to the encoding of bulk-quantum states by boundary-states expected in the AdS/CFT correspondence. In particular, the HaPPY code (or rather the tensor network that defines it) exhibits a discretized form of the Ryu-Takayanagi formula for holographic entanglement entropy.

Concretely, the the HaPPY code subspace is the image of the linear map formed by:

From Harlow 18

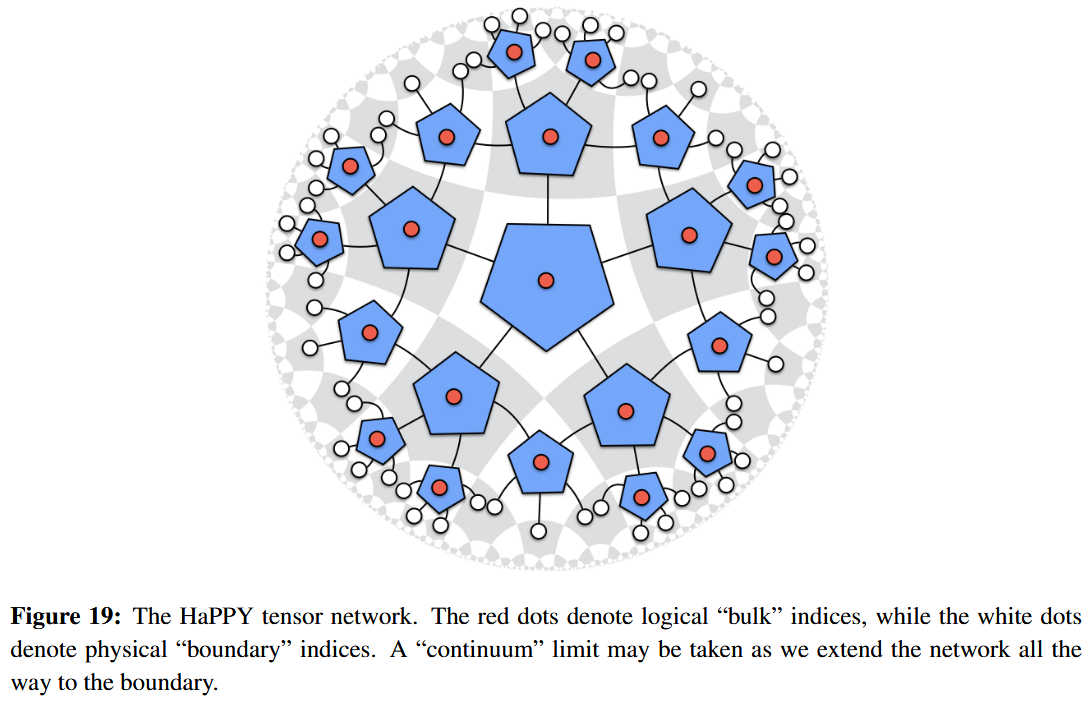
  1. picking a perfect tensor TT of rank 6;

  2. picking a finite cutoff of the pentagonal tesselation of the hyperbolic plane;

  3. regarding its Poincaré dual graph as a tensor network (string diagram in finite-dimensional vector spaces) by

    1. assigning TT to each vertex at the center of the pentagons (show in blue), with 5 of its indices contracted with its neighbours in the hyperbolic plane,

    2. and its 6th uncontracted index remaining as an input (shown in red);

  4. regarding the uncontracted edges at the cutoff boundary as output (shown in white)

and thus as a linear map from the tensor product over the bulk-vertices to the tensor product over the edges sticking out over the boundary.

Majorana dimer codes

See at Majorana dimer code.

Classes of examples

References

General

The idea of quantum encryption based on the no-cloning theorem originates with:

Original articles on quantum error correcting codes:

Realization that quantum error correcting codes could make quantum computation practically feasible:

Operator algebraic formulation of quantum error correction:

on quantum observables:

Introduction and survey:

See also:

In the context of quantum secret sharing:

In the context of quantum communication:

On (in-)compatibility of quantum error correction with universality of quantum gates (Eastin-Knill theorem):

  • Bryan Eastin, Emanuel Knill, Restrictions on Transversal Encoded Quantum Gate Sets, Phys. Rev. Lett. 102, 110502 (2009) (arXiv:0811.4262)

  • Paul Webster, Michael Vasmer, Thomas R. Scruby, Stephen D. Bartlett, Universal Fault-Tolerant Quantum Computing with Stabiliser Codes (arXiv:2012.05260)

For quantum annealing processes:

  • Kristen L. Pudenz, Tameem Albash, Daniel A. Lidar: Error-corrected quantum annealing with hundreds of qubits, Nature Communications 5 3243 (2014) [doi:10.1038/ncomms4243]

On continuous variable quantum codes:

In relation to the SYK model:

In relation to continuous symmetries:

  • Zi-Wen Liu, Sisi Zhou, Approximate symmetries and quantum error correction (arXiv:2111.06355)

Further developments:

  • Mackenzie H. Shaw, Andrew C. Doherty, Arne L. Grimsmo, Stabilizer subsystem decompositions for single- and multi-mode Gottesman-Kitaev-Preskill codes [arXiv:2210.14919]

On relevant classical control mechanisms:

In relation to the Penrose tiling:

Relating quantum error correction to linear logic:

Experimental realization

Realization of quantum error correction in experiment, hence in actual quantum computers:

Via holographic tensor networks

First quantum error correcting codes associated with planar bulk/boundary systems:

First suggestion relating quantum error correction to black hole entropy:

Introducing the idea of quantum error correcting codes given by tensor network states:

  • Andrew J. Ferris, David Poulin, Tensor Networks and Quantum Error Correction, Phys. Rev. Lett. 113, 030501 (2014) (arXiv:1312.4578)

  • Dave Bacon, Steven T. Flammia, Aram W. Harrow, Jonathan Shi, Sparse Quantum Codes from Quantum Circuits, Proc. of STOC ‘15, pp. 327-334 (2015); IEEE Transactions on Information Theory, vol 63, no 4, pp 2464-2479, April 2017 (arXiv:1411.3334)

following observations in

Interpretation of holographic tensor networks encoding holographic entanglement entropy in models for AdS2-CFT1 duality as quantum error correcting codes:

with precursor observations in

and concrete implementation by the HaPPY code:

and possibly more generally:

Introduction of the more general Majorana dimer code:

Exposition and review:

Further discussion of holographic quantum error correcting codes:

Understanding in terms of the eigenstate thermalization hypothesis:

  • Ning Bao, Newton Cheng, Eigenstate Thermalization Hypothesis and Approximate Quantum Error Correction, JHEP 08 (2019) 152 (arXiv:1906.03669)

In relation to holographic Renyi entropy:

From tesselations of higher-dimensional hyperbolic space:

  • Vivien Londe, Anthony Leverrier, Golden codes: quantum LDPC codes built from regular tessellations of hyperbolic 4-manifolds (arXiv:1712.08578)

In view of black hole thermodynamics:

Discussion of gauge symmetry of holographic tensor networks and their quantum error correcting codes:

  • Kfir Dolev, Vladimir Calvera, Sam Cree, Dominic J. Williamson, Gauging the bulk: generalized gauging maps and holographic codes (arXiv:2108.11402)

Relation of quantum error correcting codes to the Monster vertex operator algebra and more generally to 2d SCFT and string theory:

In relation to the large N limit:

In relation to renormalization group flow:

  • Keiichiro Furuya, Nima Lashkari, Mudassir Moosa, Renormalization group and approximate error correction (arXiv:2112.05099)

In relation to fixed-point path integrals:

  • Andreas Bauer, Topological error correcting processes from fixed-point path integrals (arXiv:2303.16405)

Musings on possible implications on relations between quantum gravity and quantum information:

Last revised on September 2, 2024 at 06:08:42. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (90 revisions) Cite Print Source