nLab D=6 N=(2,0) SCFT
Context
Quantum field theory
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
According to the classification of superconformal symmetry, there should exist superconformal field theories in 6 dimensions…
(Shnider 88, also Nahm 78, see Minwalla 98, section 4.2)
…with -supersymmetry, that contain a self-dual higher gauge theory whose field configurations are connections on a 2-bundle (a circle 2-bundle with connection in the abelian case).
This was derived by Claus, Kallosh & van Proeyen 1997, in the abelian case and to low order, as the small fluctuations of the Green-Schwarz sigma-model of the M5-brane around the embedding in the asymptotic boundary of the AdS-spacetime that is the near-horizon geometry of the black M5-brane.
In accord with this the AdS7-CFT6 correspondence predicts that the nonabelian 6d theory is the corresponding theory for coincident M5-branes.
In the non-abelian case it is expected (Witten 07) that the compactification of such theories are at the heart of the phenomenon that leads to S-duality in super Yang-Mills theory and further to geometric Langlands duality (Witten 09).
Due to the self-duality a characterization of these theories by an action functional is subtle. Therefore more direct descriptions are still under investigation (for instance SSW11). Review includes (Moore11, Moore 12).
Properties
Geometric engineering
For geometric engineering of the 6d (2,0)-superconformal QFT, see at duality between M-theory on Z2-orbifolds and type IIB string theory on K3-fibrations – Geometric engineering of 6d (2,0)-SCFT.
Holographic dual
Under AdS7/CFT6 the 6d -superconformal QFT is supposed to be dual to M-theory on anti de Sitter spacetime .
See AdS/CFT correspondence for more on this.
Realization of quantum chromodynamics
See at AdS-QCD correspondence.
Solitonic 1-branes
The 5d -SCFT has tensionless 1-brane configurations. From the point of view of the ambient 11-dimensional supergravity these are the boundaries of M2-branes ending on the M5-branes. (GGT)
Compactification on a Riemann surface and AGT correspondence
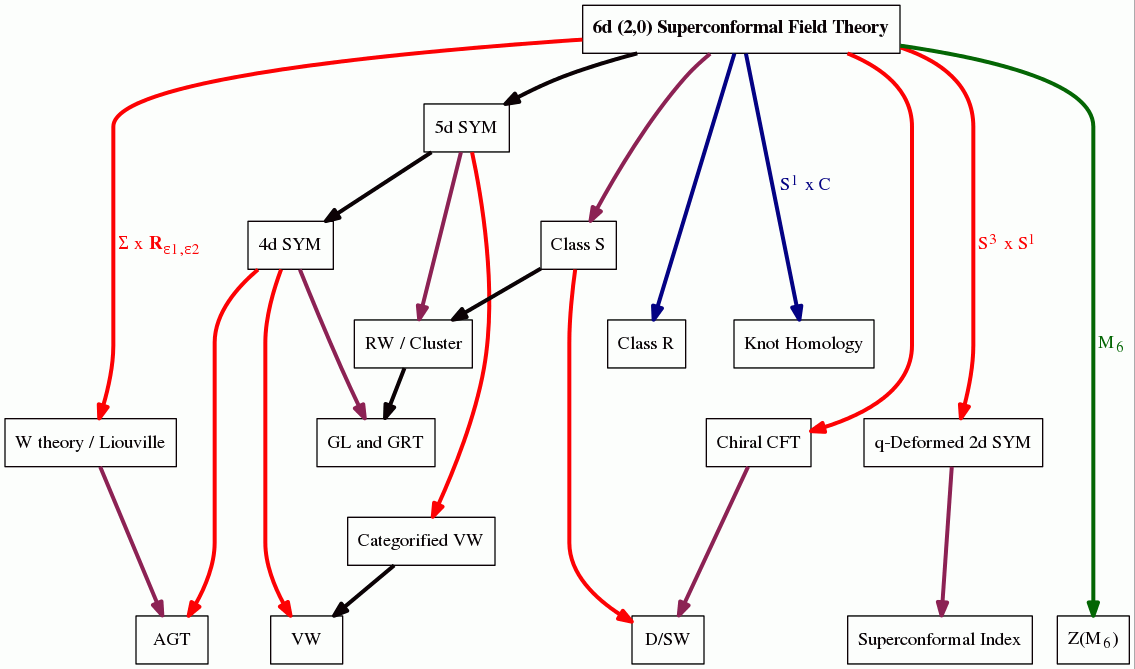
(graphics taken from (Workshop 14))
The compactification of the 5-brane on a Riemann surface yields as worldvolume theory N=2 D=4 super Yang-Mills theory. See at N=2 D=4 SYM – Construction by compactification of 5-branes.
The AGT correspondence relates the partition function of -N=2 D=4 super Yang-Mills theory obtained by compactifying the M5-brane theory on a Riemann surface of genus with punctures to 2d Liouville theory on .
More generally, this kind of construction allows to describe the 6d (2,0)-theory as a “2d SCFT with values in 4d SYM”. See at AGT correspondence for more on this.
Twistor space description
Famously the solutions to self-dual Yang-Mills theory in dimension 4 can be obtained as images of degree-2 cohomology classes under the Penrose-Ward twistor transform. Since the 6d QFT on the M5-brane contains a 2-form self-dual higher gauge field it seems natural to expect that it can be described by a higher analogy of the twistor transform. For references exploring this idea see at twistor space – References – Application to the self-dual 2-form field in 6d.
Related entries
gauge theory induced via AdS-CFT correspondence
| M-theory perspective via AdS7-CFT6 | F-theory perspective |
|---|---|
| 11d supergravity/M-theory | |
| Kaluza-Klein compactification on | compactificationon elliptic fibration followed by T-duality |
| 7-dimensional supergravity | |
| topological sector | |
| 7-dimensional Chern-Simons theory | |
| AdS7-CFT6 holographic duality | |
| 6d (2,0)-superconformal QFT on the M5-brane with conformal invariance | M5-brane worldvolume theory |
| KK-compactification on Riemann surface | double dimensional reduction on M-theory/F-theory elliptic fibration |
| N=2 D=4 super Yang-Mills theory with Montonen-Olive S-duality invariance; AGT correspondence | D3-brane worldvolume theory with type IIB S-duality |
| topological twist | |
| topologically twisted N=2 D=4 super Yang-Mills theory | |
| KK-compactification on Riemann surface | |
| A-model on , Donaldson theory |
(Shnider 88, also Nahm 78, see Minwalla 98, section 4.2)
References
See also the references at M5-brane.
General
The first indication of a 6d theory with a self-dual 2-form field appears in
- Edward Witten, section 1 of Some comments on string dynamics (hepth/9507121)
Derivation of the abelian 6d theory to low order as the small fluctuations of the Green-Schwarz sigma-model of the M5-brane around a solution embedding as the asymptotic boundary of the AdS-spacetime near-horizon geometry of a black 5-brane is due to
- Piet Claus, Renata Kallosh, Antoine Van Proeyen, M 5-brane and superconformal tensor multiplet in 6 dimensions, Nucl. Phys. B 518 (1998) 117-150 [doi:10.1016/S0550-3213(98)00137-0, arXiv:hep-th/9711161]
General survey:
-
Greg Moore, On the role of six‐dimensional -theories in recent developments in Physical Mathematics, talk at Strings 2011 (pdf slides)
-
Greg Moore, Applications of the six-dimensional (2,0) theories to Physical Mathematics, Felix Klein lectures Bonn (2012) (pdf, pdf)
-
Qiaochu Yuan: lecture notes for Mathematical Aspects of Six-Dimensional Quantum Field Theories, Berkeley, December 8th-12th, 2014 at the University of California, Berkeley
Discussion of anomaly cancellation:
-
Kantaro Ohmori, Hiroyuki Shimizu, Yuji Tachikawa, Kazuya Yonekura, Anomaly polynomial of general 6d SCFTs, Progress of Theoretical and Experimental Physics, Volume 2014, Issue 10, October 2014, 103B07 (arXiv:1408.5572)
-
Hiroyuki Shimizu, Aspects of anomalies in 6d superconformal field theories, Tokyo 2018 (spire:1802462, pdf)
Review of construction from F-theory KK-compactification:
- Jonathan Heckman, Tom Rudelius, Top Down Approach to 6D SCFTs, J. Phys. A: Math. Theor. 52 (2018) 093001 [arXiv:1805.06467, doi:10.1088/1751-8121/aafc81]
On the absence of perturbation theory:
- Chi-Ming Chang, 5d and 6d SCFTs Have No Weak Coupling Limit, J. High Energ. Phys. 2019 16 (2019) [arXiv:1810.04169, doi:10.1007/JHEP09(2019)016]
New approach to construction of candidate Lagrangian densities for D=6 N=(2,0) SCFTs:
- Neil Lambert, Lagrangian Structures, Physics Letters B 798 (2019) 134948 [arXiv:1908.10752, doi;10.1016/j.physletb.2019.134948]
Compactification to 5d super-Yang-Mills
KK-compactification on circle fibers to D=5 super Yang-Mills theory is discussed in (see also at Perry-Schwarz Lagrangian):
-
Nathan Seiberg, Sec. 7 of: Notes on Theories with 16 Supercharges, Nucl. Phys. Proc. Suppl. 67 (1998) 158-171 [arXiv:hep-th/9705117]
-
Michael Douglas, On D=5 super Yang-Mills theory and (2,0) theory, JHEP 1102:011, 2011 (arXiv:1012.2880)
-
Neil Lambert, Constantinos Papageorgakis, Maximilian Schmidt-Sommerfeld, M5-Branes, D4-Branes and Quantum 5D super-Yang-Mills, JHEP 1101:083, 2011 (arXiv:1012.2882)
-
Edward Witten, Sections 4 and 5 of Fivebranes and Knots (arXiv:1101.3216)
-
Shan Hu, 6D theory and M5 branes: A KK mode approach, 2013 (hdl:1969.1/151094)
-
Chris Hull, Neil Lambert, Emergent Time and the M5-Brane, JHEP06(2014)016 (arXiv:1403.4532)
-
Andreas Gustavsson, Five-dimensional Super-Yang-Mills and its Kaluza-Klein tower. JHEP01(2019)222 (arXiv:1812.01897)
-
Neil Lambert, Sec. 3.1 and 3.4.3. of Lessons from M2’s and Hopes for M5’s, Proceedings of the LMS-EPSRC Durham Symposium: Higher Structures in M-Theory, August 2018 Fortschritte der Physik Volume 67, Issue 8-9 2019 (arXiv:1903.02825, doi:10.1002/prop.201910011, slides pdf, video recording)
Compactification to 4d super-Yang-Mills
KK-compactification of the -CFT on torus fibers to D=4 super Yang-Mills theory and the related electric-magnetic duality/S-duality in 4-dimensions:
- Edward Witten, Conformal field theory in four and six dimensions in Ulrike Tillmann (ed.) Topology, geometry and quantum field theory LMS Lecture Note Series (2004) (arXiv:0712.0157)
and the resulting relation to the geometric Langlands correspondence:
- Edward Witten, Geometric Langlands From Six Dimensions, in Peter Kotiuga (ed.) A Celebration of the Mathematical Legacy of Raoul Bott, CRM Proceedings & Lecture Notes 50 AMS (2010) [arXiv:0905.2720, ISBN:978-0-8218-4777-0]
For more references on this see at N=2 D=4 super Yang-Mills theory the section References - Constructions from 5-branes.
Relation to BFSS matrix model on tori:
- Micha Berkooz, Moshe Rozali, Nathan Seiberg, Matrix Description of M-theory on and (arXiv:hep-th/9704089)
The KK-compactification specifically of the D=6 N=(1,0) SCFT to D=4 N=1 super Yang-Mills:
-
Ibrahima Bah, Christopher Beem, Nikolay Bobev, Brian Wecht, Four-Dimensional SCFTs from M5-Branes (arXiv:1203.0303)
-
Shlomo S. Razamat, Cumrun Vafa, Gabi Zafrir, from , J. High Energ. Phys. (2017) 2017: 64 (arXiv:1610.09178)
-
Ibrahima Bah, Amihay Hanany, Kazunobu Maruyoshi, Shlomo S. Razamat, Yuji Tachikawa, Gabi Zafrir, from on a torus with fluxes (arXiv:1702.04740)
-
Hee-Cheol Kim, Shlomo S. Razamat, Cumrun Vafa, Gabi Zafrir, E-String Theory on Riemann Surfaces, Fortsch. Phys. (arXiv:1709.02496)
-
Hee-Cheol Kim, Shlomo S. Razamat, Cumrun Vafa, Gabi Zafrir, D-type Conformal Matter and SU/USp Quivers, JHEP06(2018)058 (arXiv:1802.00620)
-
Hee-Cheol Kim, Shlomo S. Razamat, Cumrun Vafa, Gabi Zafrir, Compactifications of ADE conformal matter on a torus, JHEP09(2018)110 (arXiv:1806.07620)
-
Shlomo S. Razamat, Gabi Zafrir, Compactification of 6d minimal SCFTs on Riemann surfaces, Phys. Rev. D 98, 066006 (2018) (arXiv:1806.09196)
-
Jin Chen, Babak Haghighat, Shuwei Liu, Marcus Sperling, 4d from 6d D-type , J. High Energ. Phys. 2020 152 (2020) [arXiv:1907.00536, doi:10.1007/JHEP01(2020)152]
Compactification to 2d CFT
On KK-compactification of D=6 N=(2,0) SCFT on 4-manifolds to 2d CFTs:
-
Abhijit Gadde, Sergei Gukov, Pavel Putrov, Fivebranes and 4-manifolds, in: Arbeitstagung Bonn 2013, Progress in Mathematics 319, Birkhäuser (2016) [arXiv:1306.4320, doi:10.1007/978-3-319-43648-7_7]
-
Mykola Dedushenko, Sergei Gukov, Pavel Putrov, Vertex algebras and 4-manifold invariants, Chapter 11 in: Geometry and Physics: Volume I (2018) 249–318 [arXiv:1705.01645, doi:10.1093/oso/9780198802013.003.0011]
-
Boris Feigin, Sergei Gukov, , J. Math. Phys. 61 012302 (2020) [arXiv:1806.02470, doi:10.1063/1.5100059]
In relation to M5-brane elliptic genus:
- Sergei Gukov, Du Pei, Pavel Putrov, Cumrun Vafa, 4-manifolds and topological modular forms, J. High Energ. Phys. 2021 84 (2021) [arXiv:1811.07884, doi:10.1007/JHEP05(2021)084, spire:1704312]
and in relation to defects:
- Jin Chen, Wei Cui, Babak Haghighat, Yi-Nan Wang, SymTFTs and Duality Defects from 6d SCFTs on 4-manifolds, JHEP 2023 208 (2023) [arXiv:2305.09734, doi:10.1007/JHEP11(2023)208]
ADE classification
Discussion of the ADE classification of the 6d theories includes, after (Witten95)
-
Julie D. Blum, Kenneth Intriligator, New Phases of String Theory and 6d RG Fixed Points via Branes at Orbifold Singularities, Nucl.Phys.B506:199-222,1997 (arXiv:hep-th/9705044)
-
Jonathan Heckman, David Morrison, Cumrun Vafa, On the Classification of 6D SCFTs and Generalized ADE Orbifolds (arXiv:1312.5746)
Models and special properties
Realization of the 6d theory in F-theory is discussed in (Heckmann-Morrison-Vafa 13).
A proposal for related higher nonabelian differential form data is made in
- Henning Samtleben, Ergin Sezgin, Robert Wimmer, (1,0) superconformal models in six dimensions, J. High Energ. Phys. 2011 62 (2011) [arXiv:1108.4060, doi:10.1007/JHEP12(2011)062]
Since by transgression every nonabelian principal 2-bundle/gerbe gives rise to some kind of nonabelian 1-bundle on loop space it is clear that some parts (but not all) of the nonabelian gerbe theory on the 5-brane has an equivalent reformulation in terms of ordinary gauge theory on the loop space of the 5-brane and possibly for gauge group the loop group of the original gauge group.
Comments along these lines have been made in
- Andreas Gustavsson, Selfdual strings and loop space Nahm equations (arXiv:0802.3456).
In fact, via the strict 2-group version of the string 2-group there is a local gauge in which the loop group variables appear already before transgression of the 5-brane gerbe to loop space. This is discussed from a holographic point of view in
On the holographic dual
The basics of the relation of the 6d theory to a 7d theory under AdS-CFT is reviewed holographic duality
- Juan Maldacena, The Large N limit of superconformal field theories and supergravity, Adv. Theor. Math. Phys. 2:231, 1998, hep-th/9711200; Wilson loops in Large N field theories, Phys. Rev. Lett. 80 (1998) 4859, hep-th/9803002
The argument that the abelian 7d Chern-Simons theory of a 3-connection yields this way the conformal blocks of the abelian self-dual higher gauge theory of the 6d theory on a single brane is due to
-
Edward Witten, Five-Brane Effective Action In M-Theory J. Geom. Phys.22:103-133,1997 (arXiv:hep-th/9610234)
-
Edward Witten, AdS/CFT Correspondence And Topological Field Theory JHEP 9812:012,1998 (arXiv:hep-th/9812012)
The nonabelian generalization of this 7d action functional that follows from taking the quantum corrections (Green-Schwarz mechanism and flux quantization) of the supergravity C-field into account is discussed in
See also
-
Eric D'Hoker, John Estes, Michael Gutperle, Darya Krym,
Exact Half-BPS Flux Solutions in M-theory I Local Solutions (arXiv:0806.0605)
Exact Half-BPS Flux Solutions in M-theory II: Global solutions asymptotic to (arXiv:0810.4647)
Solitonic 1-brane excitations
-
Jerome Gauntlett, Joaquim Gomis, Paul Townsend, BPS Bounds for Worldvolume Branes (arXiv:hep-th/9711205)
-
Paul Howe, Neil Lambert, Peter West, The Threebrane Soliton of the M-Fivebrane (arXiv:hep-th/9710033)
The , SCFT as an extended functorial field theory
On the (conjectural) suggestion to view at least some aspects of the D=6 N=(2,0) SCFT (such as its quantum anomaly or its image as a 2d TQFT under the AGT correspondence) as a functorial field theory given by a functor on a suitable cobordism category, or rather as an extended such FQFT, given by an n-functor (at least a 2-functor on a 2-category of cobordisms):
-
Edward Witten, Section 1 of: Geometric Langlands From Six Dimensions, in Peter Kotiuga (ed.) A Celebration of the Mathematical Legacy of Raoul Bott, CRM Proceedings & Lecture Notes Volume: 50, AMS 2010 (arXiv:0905.2720, ISBN:978-0-8218-4777-0)
-
Daniel Freed, 4-3-2 8-7-6, talk at ASPECTS of Topology Dec 2012 (pdf, pdf)
-
Daniel Freed, p. 32 of: The cobordism hypothesis, Bulletin of the American Mathematical Society 50 (2013), pp. 57-92, (arXiv:1210.5100, doi:10.1090/S0273-0979-2012-01393-9)
-
Daniel Freed, Constantin Teleman: Relative quantum field theory, Commun. Math. Phys. 326 (2014) 459–476 [doi:10.1007/s00220-013-1880-1, arXiv:1212.1692]
-
David Ben-Zvi: Theory and Geometric Representation Theory, talks at Mathematical Aspects of Six-Dimensional Quantum Field Theories IHES 2014, notes by Qiaochu Yuan (pdf, pdf, pdf)
-
David Ben-Zvi, Algebraic geometry of topological field theories, talk at Reimagining the Foundations of Algebraic Topology April 07, 2014 - April 11, 2014 (web video)
-
Lukas Müller, Extended Functorial Field Theories and Anomalies in Quantum Field Theories (arXiv:2003.08217)
Last revised on August 28, 2024 at 07:16:01. See the history of this page for a list of all contributions to it.