nLab topological G-space
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
In the context of topology, a topological -space (traditionally just -space, for short, if the context is clear) is a topological space equipped with an action of a topological group – the equivariance group (usually taken to be the topological group underlying a compact Lie group, such as a finite group).
The canonical homomorphisms of topological -spaces are -equivariant continuous functions, and the canonical choice of homotopies between these are -equivariant continuous homotopies (for trivial -action on the interval).
A -equivariant version of the Whitehead theorem says that on G-CW complexes these -equivariant homotopy equivalences are equivalently those maps that induce weak homotopy equivalences on all fixed point spaces for all subgroups of (compact subgroups, if is allowed to be a Lie group).
By Elmendorf's theorem, this, in turn, is equivalent to the (∞,1)-presheaves over the orbit category of . See below at In topological spaces – Homotopy theory.
See (Henriques-Gepner 07) for expression in terms of topological groupoids/orbispaces.
In the context of stable homotopy theory the stabilization of -spaces is given by spectra with G-action; these lead to equivariant stable homotopy theory. See there for more details. (But beware that in this context one considers the richer concept of G-spectra, which have a forgetful functor to spectra with G-action but better homotopy theoretic properties. ) The union of this as is allowed to vary is the global equivariant stable homotopy theory.
Properties
Change of equivariance groups
In the following is a cartesian closed convenient category of topological spaces, such as that of compactly generated topological spaces.
We discuss how any homomorphism of topological groups induces an adjoint triple of functors between the corresponding (e.g. May 96, Sec. I.1, DHLPS 19, p.8, see also at induced representation for a formulation in homotopy type theory)
Throughout, let TopologicalGroups and consider a continuous homomorphism of topological groups
Pullback action
Definition
(pullback action)
Given a topological group homomorphism (1), write
for the functor which takes a topological G2-space to the same underlying topological space , equipped with the -action .
Example
(restricted action)
For a subgroup-inclusion, the pullback action in Def. is obtained by restricting the -action to that of its subgroup .
Induced action
Definition
(induced action)
Given a topological group homomorphism (1), the induced action functor
sends to the quotient space of its Cartesian product with by the diagonal action of (which on is by inverse right multiplication through ):
and equipped with the -action given by left multiplication on the -factor.
Example
(Quotients as induced actions)
If is the terminal morphism to the trivial group, then its induced action (Def. ) is the operation of forming -quotient spaces (the -orbit-space):
Proposition
(induced action is left adjoint to pullback action)
Given a topological group homomorphism (1), the induced action functor (Def. ) is left adjoint to the pullback action functor (Def. ):
Proof
For a -space and a -space, consider a -equivariant function out of the induced action
Since the -orbit of
is the entire domain space on the left, by equivariance, this function is completely determined by its restriction along this inclusion to a -equivariant function , hence to a homomorphism . This correspondence
is clearly a natural bijection and hence establishes the hom-isomorphisms characterizing the adjunction.
Coinduced action
Definition
(coinduced action)
Given a topological group homomorphism (1), the coinduced action functor
sends to the -fixed locus in the mapping space between topological spaces equipped with -actions (on the -induced left multiplication action) and itself equipped with the -action given by
Example
(Fixed loci as coinduced actions)
Let be a topological subgroup and consider the group homomorphism (1) to be the -quotient group coprojection from the normal subgroup :
Then for any -space (which in practice will usually be a -space after restriction of its action along , Example ) we have that its coinduced action (Def. ) is its -fixed locus equipped with its residual -action:
Proposition
(coinduced action is right adjoint to pullback action)
Given a topological group homomorphism (1), the pullback action functor (Def. ) is the left adjoint and the coinduced action functor (Def. ) is the right adjoint in a pair of adjoint functors
Proof
To see the defining hom-isomorphism, consider a -equivariant continuous function
From this we obtain the following function
where denotes the neutral element.
This is manifestly:
-
well-defined, due to the -equivariance of ;
-
continuous, being built from composition of continuous map;
-
-equivariant with respect to the action (2).
Conversely, given a -equivariant continuous function , we obtain the following function
This is:
-
continuous, being the composition of continuous functions;
-
-equivariant due to the equivariance properties of :
Finally, it is clear that these transformations are natural, hence it only remains to see that they are bijective:
Plugging in the above constructions we find indeed:
and
Remark
For the analogous statement of cofree-actions of simplicial groups on simplicial sets see at Borel model structure this Prop..
Fixed loci with residual Weyl group action
Combining these change-of-equivariance grouo adjunctions (from above) to “pull-push” through the correspondence
we obtain the fixed locus-functor in the form in which it appears in Elmendorf's theorem, namely with the residual Weyl group-action on the fixed loci:
Example
(Fixed loci with residual Weyl-group action as coinduced action)
Let be a subgroup-inclusion. Write
-
for the corresponding normalizer subgroup inclusion
-
for the coprojection to its quotient group by (the “Weyl group” of ).
Then the composite of
-
forming the pullback action (Def. ) along (the restricted action, Example )
-
forming the coinduced action (Def. ) along (the passage to fixed loci, Example )
is the passage to the -fixed locus equipped with its residual Weyl group-action, and Prop. with Prop. shows that this construction is a right adjoint:
Limits and colimits
Recalling that the ambient category is assumed to be a cartesian closed convenient category of topological spaces, such as that of compactly generated topological spaces:
Proposition
(forgetful functor to spaces creates all limits and colimits)
The forgetful functor from -spaces to underlying spaces creates all limits and colimits.
Proof
Topological -spaces are equivalently the algebras over the monad , which is the composite of the two left adjoints in the change-of-group adjoint triple above along . Since left adjoints preserve colimits, so does this monad.
Now the forgetful functor in question is the respective monadic functor and a general theorem (this Prop.) says that monadic functors create all limits that exist in their codomain and those colimits which exist there and are preserved by the monad.
Proposition
(compactly generated topological -spaces form a regular category)
For denoting the category of compactly generated weakly Hausdorff spaces or compactly generated Hausdorff spaces, and for a topological group, the category of topological -spaces is a regular category.
Proof
By this Prop. the given convenient category of topological spaces is regular. Since regularity is purely a condition on limits and colimits (this Def.) it transfers along any forgetful functor which creates limits and colimits. Therefore the statement follows by Prop. .
Lemma
(recognition of cartesian quotient projections) Let be a compact topological group and let be morphism of Hausdorff -spaces.
Then its quotient naturality square
is a pullback square if and only if preserves isotropy groups, i.e. if and only if for each we have
as an isomorphism of stabilizer subgroups of .
Remark
The assumption in Lemma is met in particular when the action on both sides is free, whence all isotropy groups are trivial.
This is the case in which and are -principal bundles without, however, necessarily needing to be locally trivial for Lemma to apply (“Cartan principal bundles”).
On the other hand, even if is not compact but and are -principal bundles which are locally trivial, then it follows again that (3) is a pullback (since then the universal comparison morphism is a morphism of locally trivial principal bundles over the common base space , which is an isomorphism since it is so on any open cover over which both and trivialize).
Equivariant Tietze extension theorem
See at equivariant Tietze extension theorem
Model structure and homotopy theory
The standard homotopy theory on -spaces used in equivariant homotopy theory considers weak equivalences which are weak homotopy equivalence on all (ordinary) fixed loci for all suitable subgroups. This is presented by the fine model structure on topological G-spaces, which, by Elmendorf's theorem, is equivalent to (∞,1)-presheaves over the orbit category of .
On the other hand there is also the standard homotopy theory of infinity-actions, presented by the Borel model structure, in this context also called the “coarse” or “naive” equivariant model structure (Guillou).
Examples
We discuss some classes of examples of G-spaces.
Euclidean -spaces
Let be an orthogonal linear representation of a finite group on a real vector space . Then the underlying Euclidean space inherits the structure of a G-space
We may call this the Euclidean G-space associated with the linear representation .
Representation spheres
Let be an orthogonal linear representation of a finite group on a real vector space . Then the one-point compactification of the underlying Euclidean space inherits the structure of a G-space with the point at infinity a fixed point. This is called the -representation sphere
Representation tori
Let be an orthogonal linear representation of a finite group on a real vector space .
If is the point group of a crystallographic group inside the Euclidean group
then the -action on the Euclidean space descends to the quotient by the action of the translational normal subgroup lattice (this Prop.). The resulting -space is an n-torus with -action, which might be called the representation torus of
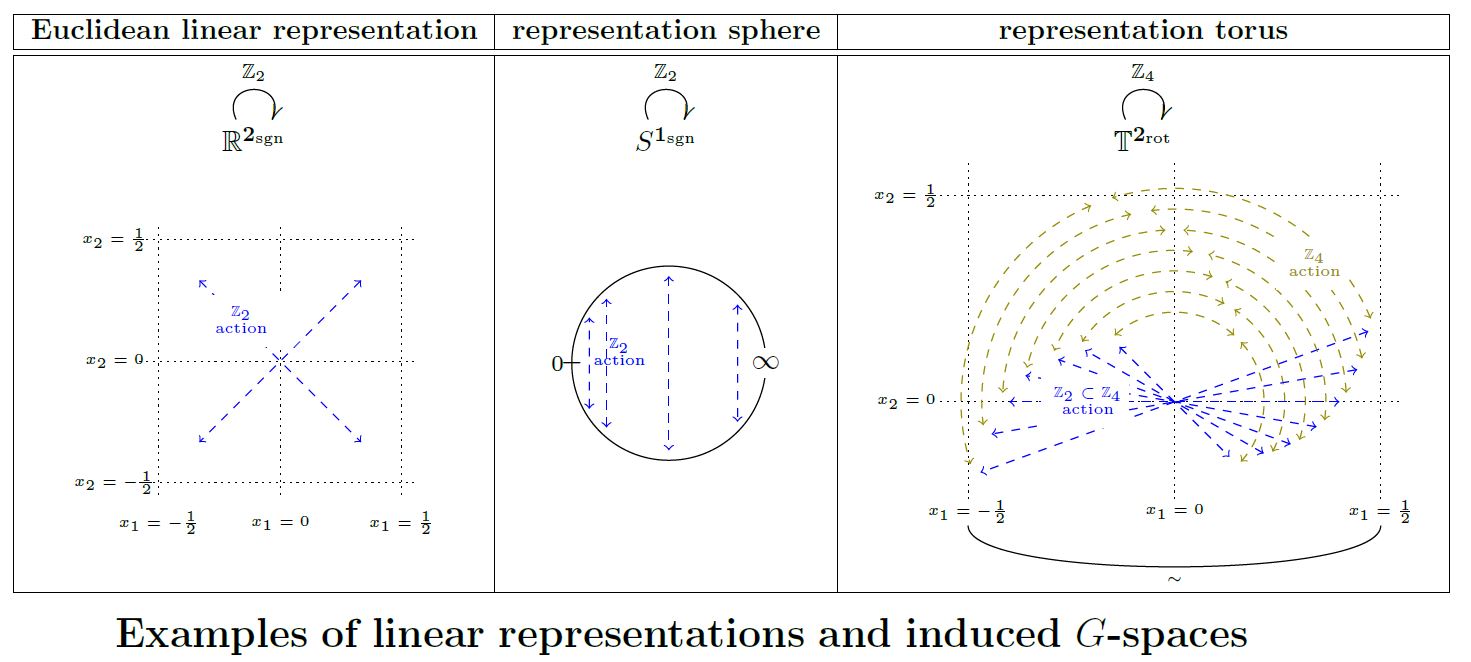
graphics grabbed from SS 19
Projective -space
Let be a finite group (or maybe a compact Lie group) and let be a -linear representation over some topological ground field .
Then the corresponding projective G-space is the quotient space of the complement of the origin in (the Euclidean space underlying) by the given action of the group of units of (from the -vector space-structure on ):
and equipped with the residual -action on (which passes to the quotient space since it commutes with the -action, by linearity).
G-CW complexes
See at G-CW complex.
Related concepts
Rezk-global equivariant homotopy theory:
See also
References
(For basics see also the references at group actions.)
Early appearance of the notion (as “transformation groups”):
-
Felix Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen (1872) Mathematische Annalen volume 43, pages 63–100 1893 (doi:10.1007/BF01446615)
English translation by M. W. Haskell:
A comparative review of recent researches in geometry, Bull. New York Math. Soc. 2, (1892-1893), 215-249. (euclid:1183407629 retyped pdf)
See also:
- Jean-Louis Koszul, Lectures on Groups of Transformations, Tata Institute 1965 (pdf, pdf)
Textbook accounts:
-
Richard Palais, The classification of -spaces, Memoirs of the AMS 36, 1960 (ISBN:978-0-8218-9979-3 pdf, pdf)
(the term “G-space” appears here)
-
Glen Bredon, Introduction to compact transformation groups, Academic Press 1972 (ISBN 9780080873596, pdf)
-
Tammo tom Dieck, Chapter 8 in: Transformation Groups and Representation Theory, Lecture Notes in Mathematics 766, Springer (1979) [doi:10.1007/BFb0085965]
-
Tammo tom Dieck, Transformation Groups, de Gruyter (1987) [doi:10.1515/9783110858372]
-
Peter May et al., Section I.1 of: Equivariant homotopy and cohomology theory, CBMS Regional Conference Series in Mathematics, vol. 91, Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1996 (ISBN: 978-0-8218-0319-6 pdf, pdf)
-
Alejandro Adem, James Davis, Topics in Transformation Groups, Chapter 1 in: Handbook of Geometric Topology, 2001, Pages 1-54 (doi:10.1016/B978-044482432-5/50002-0, pdf)
-
Stefan Schwede, Appendix B of: Global homotopy theory, New Mathematical Monographs, 34, Cambridge University Press, 2018 (doi:10.1017/9781108349161, arXiv:1802.09382)
More discussion in the context of equivariant homotopy theory:
-
Bert Guillou, A short note on models for equivariant homotopy theory (pdf, pdf)
-
André Henriques, David Gepner, Homotopy Theory of Orbispaces (arXiv:math/0701916)
-
Alexander Bykov, Raúl Juárez Flores G-fibrations and twisted products, Topology and its Applications Volume 196, Part B, December 2015, Pages 379-397 (doi:10.1016/j.topol.2015.05.011)
Specifically in the context of proper equivariant homotopy theory:
- Dieter Degrijse, Markus Hausmann, Wolfgang Lück, Irakli Patchkoria, Stefan Schwede, Proper equivariant stable homotopy theory, Memoirs of the AMS (arXiv:1908.00779)
See also the references at equivariant homotopy theory.
The special case of smooth Lie group-actions on smooth manifolds:
Lecture notes:
- Eckhard Meinrenken, Group actions on manifolds, Lecture Notes 2003 (pdf, pdf)
Last revised on August 26, 2025 at 08:29:34. See the history of this page for a list of all contributions to it.