nLab D=5 supergravity

Idea

supergravity in dimension 5. For $N = 1$ this arises from 11-dimensional supergravity by KK-compactification on a Calabi-Yau manifold of complex dimension 3 (see at M-theory on Calabi-Yau manifolds), hence serves as the low-energy effective field theory of the strong-coupling version of Calabi-Yau compactifications of type IIA string theory (see supersymmetry and Calabi-Yau manifolds)

$$\array{ 11d \; SuGra\; on\; S^1 \times Y_6 \times X_4 &\longrightarrow& 5d \; SuGra\; on\; S^1 \times X_4 && strong \; coupling \\ \downarrow && \downarrow \\ 10d\; tpye \;IIA\; Sugra\; on \; Y_6 \times X_4 &\longrightarrow& 10d\; Sugra\; on \; X_4 && weak \; coupling }$$

Properties

5d Chern-Simons term

This theory has a 2-form field strength $F_2$, locally $F_2 = d A$, with a 5d Chern-Simons theory action functional locally of the form $\propto \int_X F_2 \wedge F_2 \wedge A$ (e.g. Castellani-D’Auria-Fre (III.5.70), Gauntlet-Myers-Townsend 98, p. 3, GGHPR 02 (2.1), Bonetti-Grimm-Hohenegger 13). Hence its equation of motion is of the non-linear form

$$d F_3 = F_2 \wedge F_2$$

with $F_3 \coloneqq \star F_2$ the Hodge dual of $F_2$ (GGHPR 02 (2.2)).

This is reflected in the corresponding cochains on super Minkowski spacetime

$$\mu_{D0,5d} = \overline{\psi}_A \psi_A \phantom{AAA} \mu_{string,5d} = \overline{\psi}_A\Gamma_a \psi_A \wedge e^a$$

satisfying

$$d \mu_{string,5d} = \mu_{D0,5d} \wedge \mu_{D0,5d} \,.$$

due to the Fierz identity in Castellani-D’Auria-Fré 91 (III.5.50a), this example:

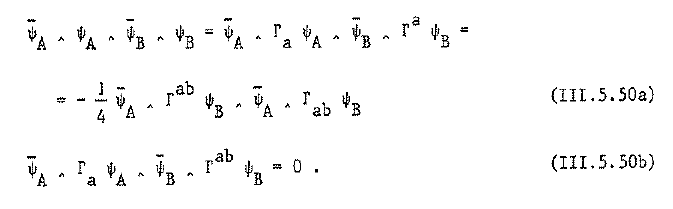
(the other Fierz identity (III.5.50a) gives the cocycle for the membrane (super 2-brane in 5d) $\mu_{membrane,5d} \coloneqq \frac{i}{2}\overline{\psi}_A \Gamma_{a b} \psi \wedge e^a \wedge e^b$, $d \mu_{membrane,5d} = 0$, that appears already in the old brane scan. )

This is a lower dimensional analogue to the situation for the C-field $G_4$ (locally $G_4 = d C$) in 11-dimensional supergravity, which has a Chern-Simons term locally of the form $\propto \int G_4 \wedge G_4 \wedge C$ and hence the equation of motion

$$d G_7 \;=\; -\tfrac{1}{2}G_4 \wedge G_4$$

with $G_7 = \star G_4$.

Black holes and black rings

The first black ring solution in 5d sugra was found in (Elvang-Emparan-Mateos-Reall 04, Elvang-Emparan-Mateos-Reall 05).

Supersymmetric black holes exist precisely only in dimensions 4 and 5 (Gauntlett-Myers-Townsend 98). These play a key role in the discussion of black holes in string theory.

(There are supersymmetric particle-like solutions of $d \gt 5$ supergravity theories that are sometimes called black holes, but these are always singular. There are also supersymmetric black holes in $d = 3$, but the spacetime in that case is asymptotically anti-de Sitter spacetime rather than asymptotically flat. Of course, there are non-singular supersymmetric black brane solutions in various $d \geq 4$ supergravity theories but these are neither ‘particle-like’ nor, strictly speaking, asymptotically flat.)

Via Calabi-Yau compactification of 11d supergravity

Discussion of 5d supergravity as a KK-compactification of 11-dimensional supergravity on a Calabi-Yau manifold of complex dimension 3 (M-theory on Calabi-Yau manifolds) is discussed in

(Hull-Townsend 95, p.30-31, Cadavid-Ceresole-D’Auria-Ferrara 95 Ferrara-Khuria-Minasian 96, Ferrara-Minasian-Sagnotti 96). See also (Mizoguchi-Ohta 98).

U-duality

	supergravity gauge group (split real form)	T-duality group (via toroidal KK-compactification)	U-duality	maximal gauged supergravity
	$SL(2,\mathbb{R})$	1	$SL(2,\mathbb{Z})$ S-duality	D=10 type IIB supergravity
	SL$(2,\mathbb{R}) \times$ O(1,1)	$\mathbb{Z}_2$	$SL(2,\mathbb{Z})$ $\times \mathbb{Z}_2$	D=9 supergravity
SU(3)$\times$ SU(2)	SL$(3,\mathbb{R}) \times SL(2,\mathbb{R})$	$O(2,2;\mathbb{Z})$	$SL(3,\mathbb{Z})\times SL(2,\mathbb{Z})$	D=8 supergravity
SU(5)	$SL(5,\mathbb{R})$	$O(3,3;\mathbb{Z})$	$SL(5,\mathbb{Z})$	D=7 supergravity
Spin(10)	$Spin(5,5)$	$O(4,4;\mathbb{Z})$	$O(5,5,\mathbb{Z})$	D=6 supergravity
E₆	$E_{6(6)}$	$O(5,5;\mathbb{Z})$	$E_{6(6)}(\mathbb{Z})$	D=5 supergravity
E₇	$E_{7(7)}$	$O(6,6;\mathbb{Z})$	$E_{7(7)}(\mathbb{Z})$	D=4 supergravity
E₈	$E_{8(8)}$	$O(7,7;\mathbb{Z})$	$E_{8(8)}(\mathbb{Z})$	D=3 supergravity
E₉	$E_{9(9)}$	$O(8,8;\mathbb{Z})$	$E_{9(9)}(\mathbb{Z})$	D=2 supergravity	E₈-equivariant elliptic cohomology
E₁₀	$E_{10(10)}$	$O(9,9;\mathbb{Z})$	$E_{10(10)}(\mathbb{Z})$
E₁₁	$E_{11(11)}$	$O(10,10;\mathbb{Z})$	$E_{11(11)}(\mathbb{Z})$

(Hull-Townsend 94, table 1, table 2)

$N = 2$ supersymmetry

Consider super Lie algebra cocoycles on $N =2$ 5d super-Minkowski spacetime (as in the brane scan).

With the notation as used at super Minkowski spacetime – Canonical coordinates, there are now two copies of spinor-valued 1-forms, denoted $\psi_1$ and $\psi_2$. We use indices of the form $A,B, \cdots$ for these. Then the non-trivial bit of the Chevalley-Eilenberg algebra differential for $N = 2$, $d = 5$ super Minkowski spacetime is

$$d_{CE} e^a = - \tfrac{i}{2} \overline{\psi}_A \wedge \Gamma^a \psi_A$$

where summation over repeated indices is understood.

There is a Fierz identity

$$\overline{\psi}_A \wedge \psi_A \wedge \overline{\psi}_B \wedge \psi_B \;=\; \overline{\psi}_A \wedge \Gamma_a \psi_A \wedge \overline{\psi}_B \wedge \Gamma^a \psi_B \,.$$

(Castellani-D’Auria-Fré (III.5.50a))

This implies that

$$d_{CE} (\overline{\psi}_A \Gamma^a \psi_A \wedge e_a) \;\propto\; (\overline{\psi}_A \wedge \Gamma^a \psi_A) \wedge (\overline{\psi}_B \wedge \Gamma^a \psi_B) \,.$$

There is a 4-cocycle of the form

$$\mu_2 = \epsilon^{A B} \overline{\psi}_A \wedge \Gamma^{a b} \psi_B \wedge e_a \wedge e_b \,.$$

(Castellani-D’Auria-Fré (III.5.50b), (III.5.53c))

Related concepts

• supergravity

  • D=2 supergravity

  • D=3 supergravity

  • D=4 supergravity

  • D=5 supergravity

    • super 2-brane in 5d

  • D=6 supergravity

  • D=7 supergravity

  • D=8 supergravity

  • D=9 supergravity

  • D=10 supergravity

  • D=11 supergravity

    • D=11 N=1 supergravity

• D=5 gravity

• D=5 Chern-Simons theory

• 10-dimensional type II supergravity, heterotic supergravity

References

Construction of 5d gauged supergravity via D'Auria-Fré formulation of supergravity is in

• Laura Andrianopoli, Francesco Cordaro, Pietro Fré, Leonardo Gualtieri, Non-Semisimple Gaugings of D=5 N=8 Supergravity and FDA.s, Class. Quant. Grav. 18 (2001) 395-414 [arXiv:hep-th/0009048]

surveyed in

• Laura Andrianopoli, Francesco Cordaro, Pietro Fré, Non-Semisimple Gaugings of D=5 N=8 Supergravity, Fortsch.Phys.49:511-518,2001 (arXiv:hep-th/0012203)

General

General discussion:

• Leonardo Castellani, Riccardo D'Auria, Pietro Fré, chapter III.5 of Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991)

  (in D'Auria-Fre formulation of supergravity)

• William Linch III, Markus A. Luty, J. Phillips, Five dimensional supergravity in $N = 1$ superspace, Phys.Rev.D68:025008,2003 (arXiv:hep-th/0209060)

• Jerome Gauntlett, Jan Gutowski, Christopher Hull, Stathis Pakis, Harvey Reall, All supersymmetric solutions of minimal supergravity in five dimensions, Class. Quant. Grav. 20 (2003) 4587-4634 [arXiv:hep-th/0209114, doi:10.1088/0264-9381/20/21/005]

• Sorin Cucu, From M-theory to $D=5$ supergravity and duality-symmetric theories (arXiv:hep-th/0310105)

• Eric Bergshoeff, Sorin Cucu, Tim de Wit, Jos Gheerardyn, Stefan Vandoren, Antoine Van Proeyen, $N=2$ supergravity in five dimensions revisited (arXiv:hep-th/0403045)

• Katrin Becker, Melanie Becker, Daniel Butter, William Linch III, Stephen Randall, Five-dimensional Supergravity in N = 1/2 Superspace (arXiv:1909.09208)

• Edoardo Lauria, Antoine Van Proeyen, $\mathcal{N}=2$ Supergravity in $D=4,5,6$ Dimensions (arXiv:2004.11433)

See also:

• Andrew Beckett, José Figueroa-O'Farrill, Killing superalgebras for lorentzian five-manifolds (arxiv:2105.05775)

• Soumya Adhikari, Bindusar Sahoo, $\mathcal{N}=2$ conformal supergravity in five dimensions* [arXiv:2312.01879]

Via M-theory on Calabi-Yau 3-folds

Discussion via KK-compactification as M-theory on Calabi-Yau manifolds includes

• Chris Hull, Paul Townsend, pages 30 and 31 of Unity of Superstring Dualities, Nucl.Phys.B438:109-137,1995 (arXiv:hep-th/9410167)

• {CadavidCeresoleDAuriaFerrara95} A.C. Cadavid, A. Ceresole, Riccardo D'Auria, Sergio Ferrara, 11-Dimensional Supergravity Compactified on Calabi-Yau Threefolds (arXiv:hep-th/9506144)

• Sergio Ferrara, Ramzi R. Khuria, Ruben Minasian, M-theory on a Calabi-Yau manifold, Phys.Lett.B375:81-88,1996 (arXiv:hep-th/9602102)

• Sergio Ferrara, Ruben Minasian, Augusto Sagnotti, Low-Energy Analysis of M and F Theories on Calabi-Yau Threefolds, Nucl.Phys. B474 (1996) 323-342 (arXiv:hep-th/9604097)

• S. Mizoguchi, N. Ohta, More on the Similarity between $D=5$ Simple Supergravity and M Theory, Phys.Lett. B441 (1998) 123-132 (arXiv:hep-th/9807111)

Further discussion of the 5d Chern-Simons term includes

• Federico Bonetti, Thomas Grimm, Stefan Hohenegger, One-loop Chern-Simons terms in five dimensions (arXiv:1302.2918)

(one-loop corrections).

Via type IIB theory

• Arnaud Baguet, Olaf Hohm, Henning Samtleben, Consistent Type IIB Reductions to Maximal 5D Supergravity (arXiv:1506.01385)

Gauged sugra

The maximal 5d gauged supergravity was first constructed in

• M. Pernici, K. Pilch, Peter van Nieuwenhuizen, Gauged $N=8$ $D=5$ Supergravity, Nucl.Phys. B259 (1985) 460 (spire)

• Murat Günaydin, L. J. Romans and Nicholas Warner, Gauged $N = 8$ Supergravity in Five Dimensions, Phys. Lett. 154B, (1985) 268 (spire:207663, doi:10.1016/0370-2693(85)90361-2)

• Murat Günaydin, L. J. Romans and Nicholas Warner, Compact and Non–Compact Gauged Supergravity Theories in Five Dimensions, Nucl. Phys. B272 (1986) 598 (spire:219727, doi:10.1016/0550-3213(86)90237-3)

See (ACFG 01).

• Murat Gunaydin, Marco Zagermann, The Gauging of Five-dimensional, $N=2$ Maxwell-Einstein Supergravity Theories coupled to Tensor Multiplets, Nucl.Phys.B572:131-150,2000 (arXiv:hep-th/9912027)

• Murat Gunaydin, Marco Zagermann, The Vacua of 5d, $N=2$ Gauged Yang-Mills/Einstein/Tensor Supergravity: Abelian Case, Phys.Rev.D62:044028,2000 (arXiv:hep-th/0002228)

• A. Ceresole, Gianguido Dall'Agata, General matter coupled $N=2$, $D=5$ gauged supergravity, Nucl.Phys. B585 (2000) 143-170 (arXiv:hep-th/0004111)

• John Ellis, Murat Gunaydin, Marco Zagermann, Options for Gauge Groups in Five-Dimensional Supergravity, JHEP 0111:024,2001 (arXiv:hep-th/0108094)

Horava-Witten compactification

Discussion of KK-compactification on $S^1/(\mathbb{Z}/2)$-orbifolds (the version of Horava-Witten theory after dimensional reduction) is discussed in

• Filipe Paccetti Correia, Michael G. Schmidt, Zurab Tavartkiladze, 4D Superfield Reduction of 5D Orbifold SUGRA and Heterotic M-theory (arXiv:hep-th/0602173)

Black hole solutions

Discussion of lifts of 4d black holes to 5d black holes and black rings and embedding as black holes in string theory includes

• Jerome Gauntlett, Robert C. Myers, Paul Townsend, Black Holes of $D=5$ Supergravity, Class.Quant.Grav. 16 (1999) 1-21 [arXiv:hep-th/9810204, doi:10.1088/0264-9381/16/1/001]

• Henriette Elvang, Roberto Emparan, David Mateos, Harvey Reall, A supersymmetric black ring, Phys. Rev. Lett. 93:211302,2004 (arXiv:hep-th/0407065)

• Henriette Elvang, Roberto Emparan, David Mateos, Harvey Reall, Supersymmetric 4D Rotating Black Holes from 5D Black Rings, JHEP0508:042,2005 (arXiv:hep-th/0504125)

• Iosif Bena, Per Kraus, Microscopic description of black rings in AdS/CFT JHEP 12 (2004) 070 (hep-th/0408186)

• Iosif Bena, Per Kraus, Microstates of the D1-D5-KK system Phys. Rev. D72 (2005) 025007 (hep-th/0503053)

• Davide Gaiotto, Andrew Strominger, Xi Yin, 5D black rings and 4D black holes JHEP 02 (2006) 023 (hep-th/0504126)

• Davide Gaiotto, Andrew Strominger, Xi Yin, New connections between 4D and 5D black holes, JHEP 02 (2006) 024 (hep-th/0503217)

• Alejandra Castro, Joshua L. Davis, Per Kraus, Finn Larsen, String Theory Effects on Five-Dimensional Black Hole Physics (arXiv:0801.1863)

Review:

• Per Kraus, Lectures on black holes and the $AdS_3$/$CFT_2$ correspondence (arXiv:hep-th/0609074)

  Stringy black holes in five dimensions, 2007 (pdf slides)

Further defect branes:

• Eun Kyung Park, Pyung Seong Kwon, NS-branes in 5d brane world models, Phys. Rev. D82:046001, 2010 (arXiv:1007.1290, doi:10.1103/PhysRevD.82.046001)

• Minkyu Park, Masaki Shigemori, Codimension-2 Solutions in Five-Dimensional Supergravity, JHEP 1510 (2015) 011 (arXiv:1505.05169)

• Masaki Shigemori, Interpolating between multi-center microstate geometries, JHEP 09 (2021) 010 (arXiv:2105.11639)