nLab intersecting D-brane model
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Quantum field theory
Contents
- Idea
- Bottom-up and Top-down approaches
- Properties
- Chiral fermions
- Generations of fermions
- Yukawa couplings
- Higgs mechanism
- RR-Tadpole cancellation and Orientifolding
- Intersections of D6s with D8/O8s
- Relation to M-theory on -manifolds
- Cosmology and Holography
- Computer scan of Gepner-model compactifications
- Examples
- References
Idea
In string phenomenology for type IIA string theory, quasi-realistic models (i.e. close to the standard model of particle physics, or an MSSM) may be obtained by KK-compactifications from the 10-dimensions down to 4d with configurations of D6-branes which fill all of 4d spacetime and intersect in a certain way in the 6-dimensional fiber space.
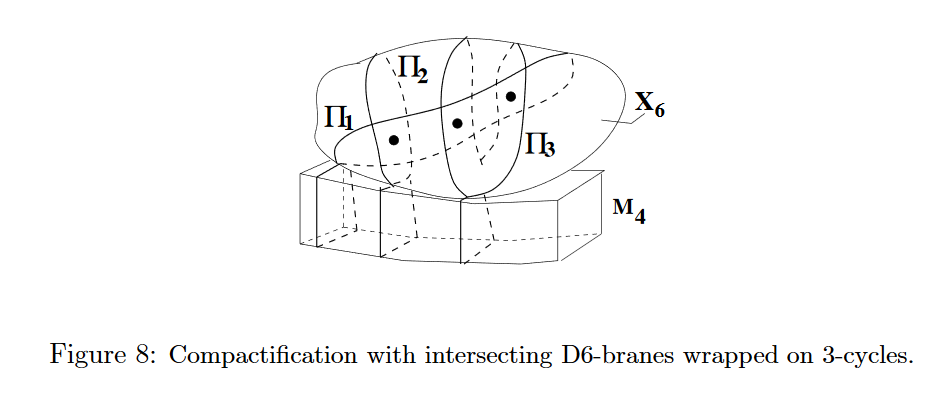
graphics grabbed from Uranga 12a, p. 12
The Chan-Paton gauge field on the D6-branes yields the gauge fields in 4d, and the precise intersection pattern determines the effective fundamental particle content in 4d.
See also at string phenomenology the section Models in type II with intersecting branes.
Bottom-up and Top-down approaches
One distinguishes bottom-up and top-down model building strategies:
snippet grabbed from Aldazabal-Ibáñez-Quevedo-Uranga 00
Properties
Chiral fermions
One of the most striking special properties of the standard model of particle physics is that its content of fermionic fundamental particles is “chiral”, in that the left and right Weyl spinor-components of the would-be Dirac spinor-representation of the quarks, electrons and neutrinos couple differently to the gauge fields (for review see e.g. Ibanez-Uranga 12, section 1.1).
The observation that such chiral fermions do indeed appear when D6-branes intersect at an angle on an is due to (Berkooz-Douglas-Leigh 96), see also (AFIRU 00, section 4, BCLS 05, section 2.3). For review with an eye towards RR-field tadpole cancellation on toroidal orientifolds see also Forste-Honecker-Schreyer 01, Honecker 01, Sec. 2, Honecker 02.
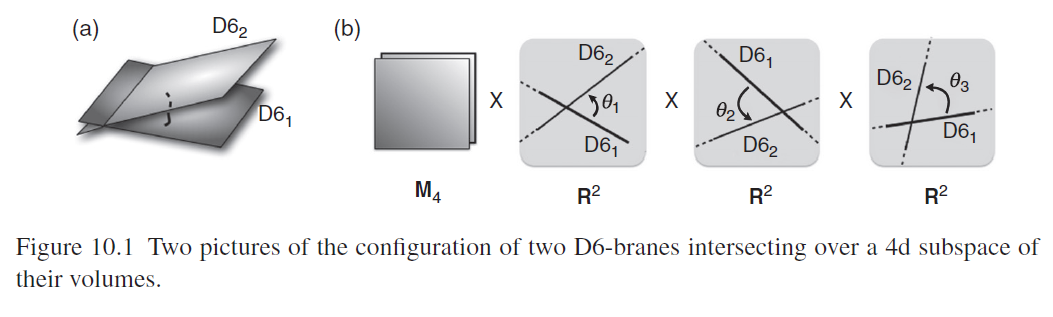
graphics grabbed from Ibáñez-Uranga 12
Vague review is in (Ibáñez-Uranga 12, section 10.2.1, Uranga 12a, section 2.3).
The lift of this situation to M-theory on G₂-manifolds is discussed in (Berglund-Brandhuber 02, Bourjaily-Espahbodi 08).
Generations of fermions
While (presently) intersecting D-brane models don’t explain why there are precisely 3 generations of fundamental particles in the standard model of particle physics, they do have the property that generically any such model does feature several generations of fundamental particles.
The reason is that in these models there is one copy of a set of fundamental particles at each intersection point of two 3-manifolds (the internal part of the D6-branes) in a compact 6-dimensional space, and generically these intersection numbers are greater than one and hence induce a finite number of generations (BCLS 05, section 2.3, Ibanez-Uranga 12, p. 307, Uranga 12a, p. 12):
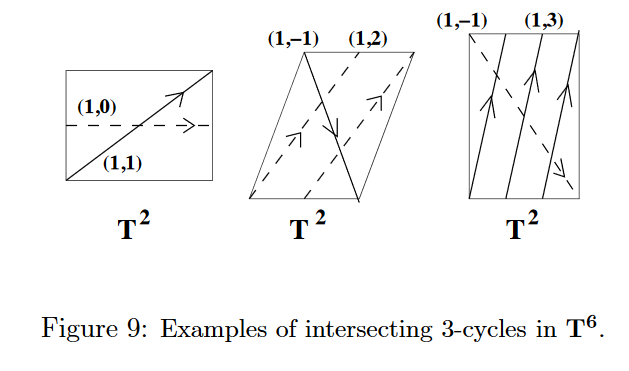
graphics grabbed from Uranga 12a, p. 13
Yukawa couplings
In intersecting D-brane models Yukawa couplings are encoded by worldsheet instantons of open strings stretching between the intersecting D-branes (see Marchesano 03, Section 7.5). Mathematically this is encoded by derived hom-spaces in a Fukaya category (see Marchesano 03, Section 7.5).
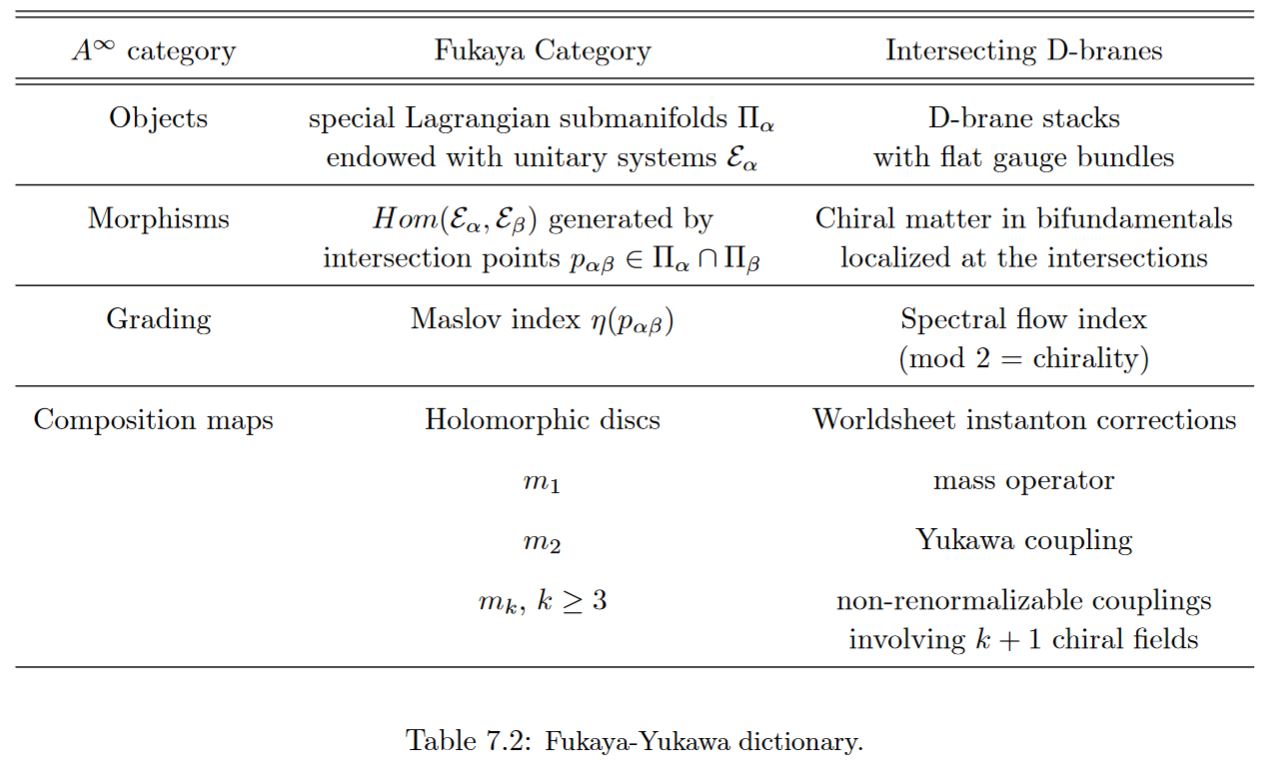
table grabbed from Marchesano 03
Realistic Yukawa couplings and fermion masses in an MSSM Pati-Salam GUT model with 3 generations of fermions realized on intersecting D6-branes KK-compactified on a toroidal orbifold are claimed in in Mayes 19, Gemill-Howington-Mayes 19, based on Chen-Li-Mayes-Nanopoulos 07a, Chen-Li-Mayes-Nanopoulos 07b.
Higgs mechanism
The Higgs mechanism naturally arises in intersecting D-brane models: The Higgs field appears here as the scalar field that witnesses in perturbation theory the process of brane recombination at the intersection locus of the D-branes (Cremades-Ibanez-Marchesano 02, section 7):
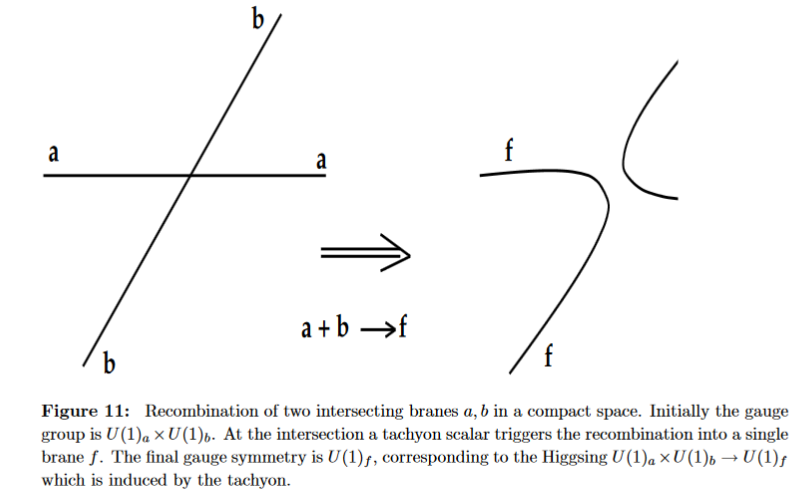
Further developments in Ibanez-Marchesano-Rabadan 01, Hebecker-Knochel-Weigand 13 and specifically via string field theory in HINSS 18.
For review see Ibanez-Uranga 12, fig 10.2:
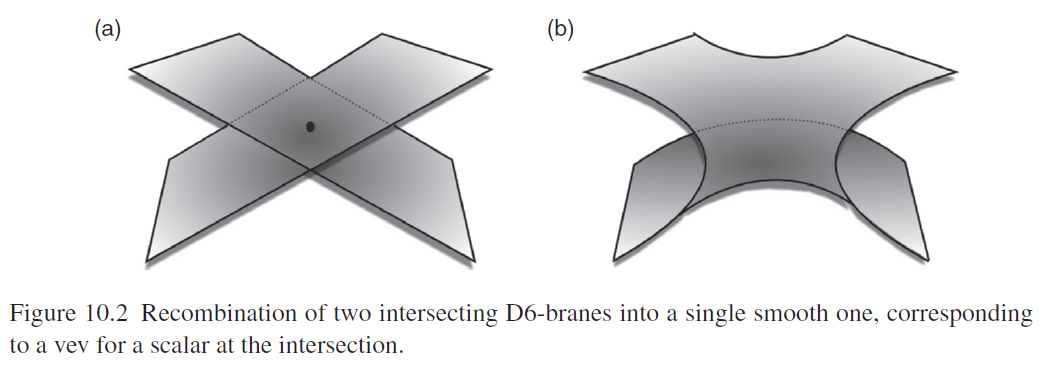
RR-Tadpole cancellation and Orientifolding
Consistent intersecting D-brane models have to be in type I string theory, or generally in type II string theory with orientifold backgrounds, to achieve RR-field tadpole cancellation.
This is a key consistency condition in intersecting D-brane model building (e.g. BCLS 05, section 2.4, Ibanez-Uranga 12, section 4.4)
RR-field tadpole cancellation conditions for D-branes wrapped on toroidal orientifolds
in terms of their D-brane charge in equivariant K-theory = representation ring
(here denotes the regular representation of dimension ord(G))
| single D-brane species on toroidal orientifold | local/twisted tadpole cancellation condition | global/untwisted tadpole cancellation condition | comment |
|---|---|---|---|
| D5-branes transv. to | (Buchel-Shiu-Tye 99 (19)) | (Buchel-Shiu-Tye 99 (18)) | following Gimon-Polchinski 96, Gimon-Johnson 96 |
| D5-branes transv. to | (Buchel-Shiu-Tye 99 (19)) | (Buchel-Shiu-Tye 99 (18)) | following Gimon-Polchinski 96, Gimon-Johnson 96 |
| D4-branes transv. to | (AFIRU 00a, 4.2.1) | ||
| D4-branes transv. to | (AFIRU 00b, (7.2)) | (Kataoka-Shimojo 01, (14)-(17) | |
| D8-branes on | | (Honecker 01, 4, Honecker 02a, (25) ∧ (28) ⇔ (29), Honecker 02b, (3.19)-(3.27)) | equivalent to D4 case by T-duality: Honecker 01, p. 2, Honecker 02a, 6, Honecker 02b, p. 15 review in: Marchesano 03, Sec. 4 |
| D6-branes on | (Ishihara-Kataoka-Sato 99, (4.16)) | ||
| D3-branes on | (Feng-He-Karch-Uranga 01, (25)) | ||
| D7-branes on | (Feng-He-Karch-Uranga 01, (5), (6)) |
Intersections of D6s with D8/O8s
A black D6-brane may end on a black NS5-brane, and in fact each black NS5-brane at a non-trivial ADE singularity has to be the junction of two black D6-branes. For details see at D6-branes ending on NS5-branes.
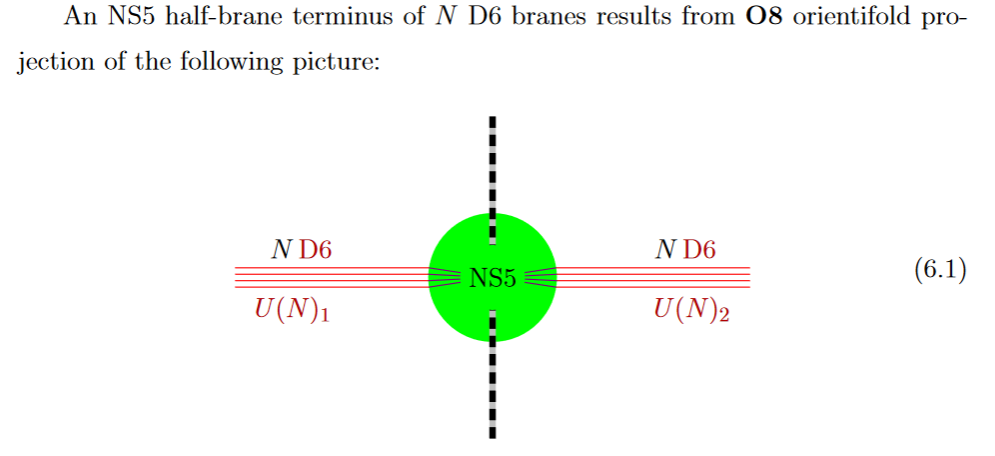
from GKSTY 02
If in addition the black NS5-brane sits at an O8-plane, hence at the orientifold fixed point-locus (see above), then in the ordinary -quotient it appears as a “half-brane” with only one copy of D6-branes ending on it:
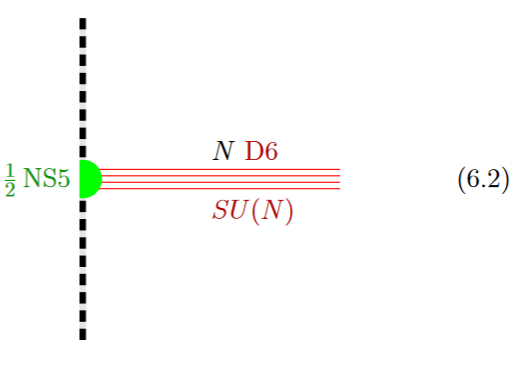
from GKSTY 02
(In Hanany-Zaffaroni 99 this is interpreted in terms of the 't Hooft-Polyakov monopole.)
The lift to M-theory of this situation is an M5-brane intersecting an M9-brane:
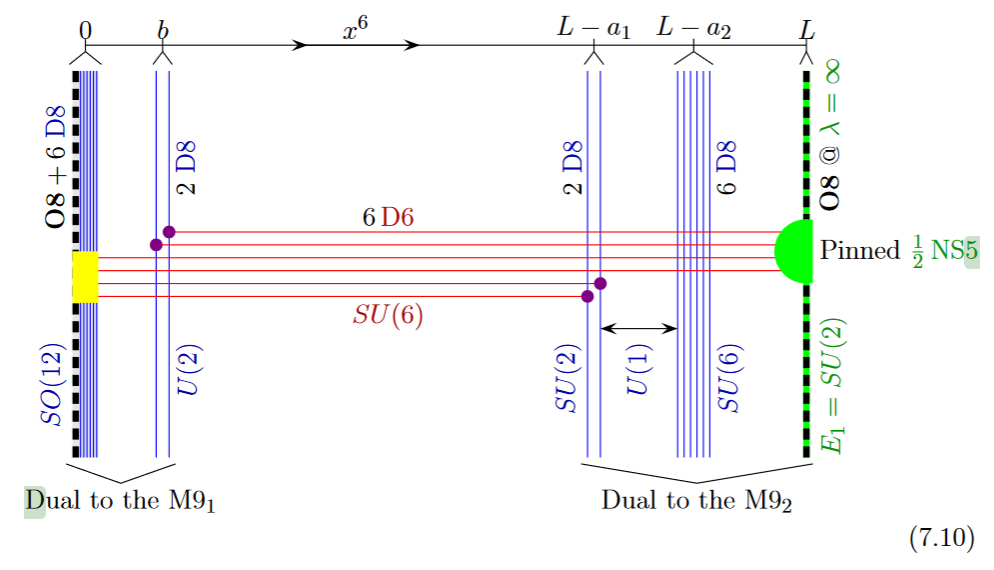
from GKSTY 02
Alternatively, the O8-plane may intersect the black D6-branes away from the black NS5-brane:
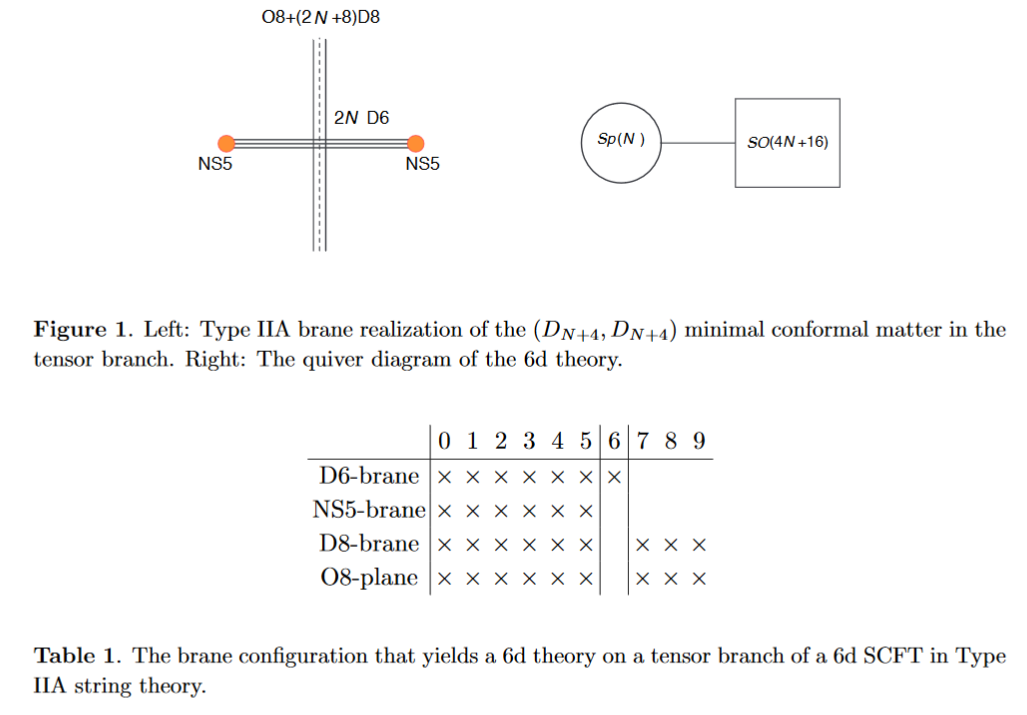
from HKLY 15
In general, some of the NS5 sit away from the O8-plane, while some sit on top of it:
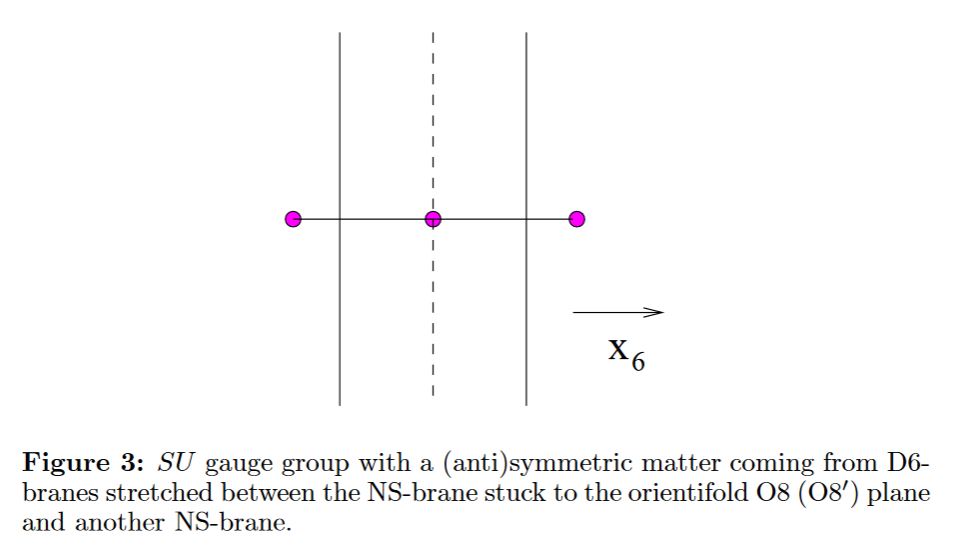
from Hanany-Zaffaroni 98
Relation to M-theory on -manifolds
Lift to M-theory on G₂-manifolds (e.g. G₂-MSSM): see references below
Cosmology and Holography
Since the near horizon geometry of BPS black branes is conformal to the Cartesian product of anti de Sitter spaces with the unit -sphere around the brane, the cosmology of intersecting D-brane models realizes the observable universe on the asymptotic boundary of an approximately anti de Sitter spacetime (see for instance Kaloper 04, Flachi-Minamitsuji 09). The basic structure is hence that of Randall-Sundrum models, but details differ, such as notably in warped throat geometries, see Uranga 05, section 18.
These warped throat models go back to Klebanov-Strassler 00 which discusses aspects of confinement in Yang-Mills theory on conincident ordinary and fractional D3-branes at the singularity of a warped conifold. See also Klebanov-Witten 98.
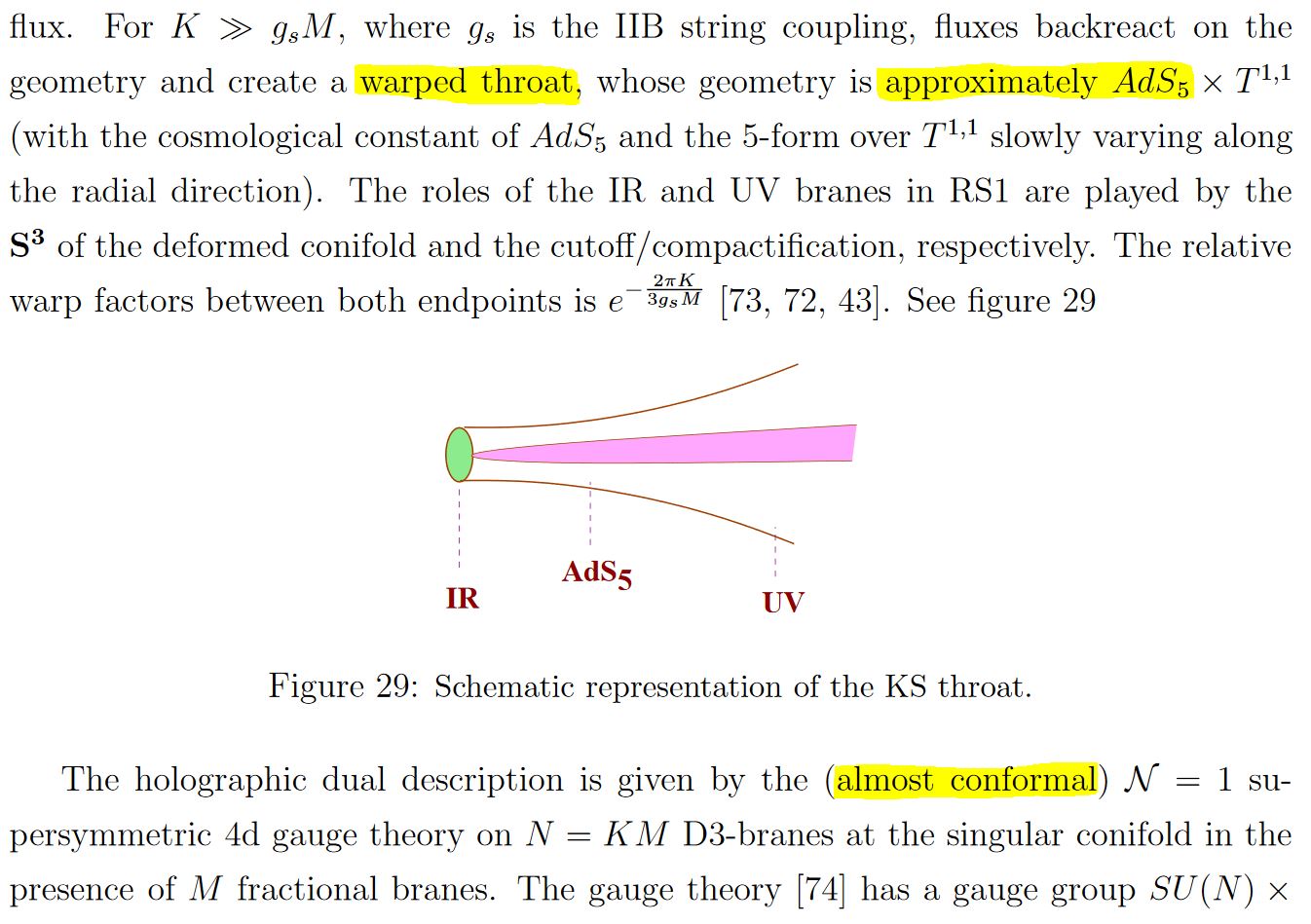
snippet grabbed from Uranga 05, section 18
here: “RS”=Randall-Sundrum model; “KS”=Klebanov-Strassler 00
In particular this means that AdS-CFT duality applies in some approximation to intersecting D-brane models (e.g. Soda 10, GHMO 16), thus allowing to compute, to some approximation, non-perturbative effects in the Yang-Mills theory on the intersecting branes in terms of gravity on the ambient warped throat AdS (Klebanov-Strassler 00, section 6)
Such approximate versions of AdS-CFT for gauge theories realized on intersecting D-branes are used for instance to estimate non-perturbative effects in QCD, such as the shear viscosity of the quark-gluon plasma (see the references there). See at AdS-QCD correspondence for more on this.
Computer scan of Gepner-model compactifications
Discussion of string phenomenology of intersecting D-brane models KK-compactified with non-geometric fibers such that the would-be string sigma-models with these target spaces are in fact Gepner models (in the sense of Spectral Standard Model and String Compactifications) is in (Dijkstra-Huiszoon-Schellekens 04a, Dijkstra-Huiszoon-Schellekens 04b):
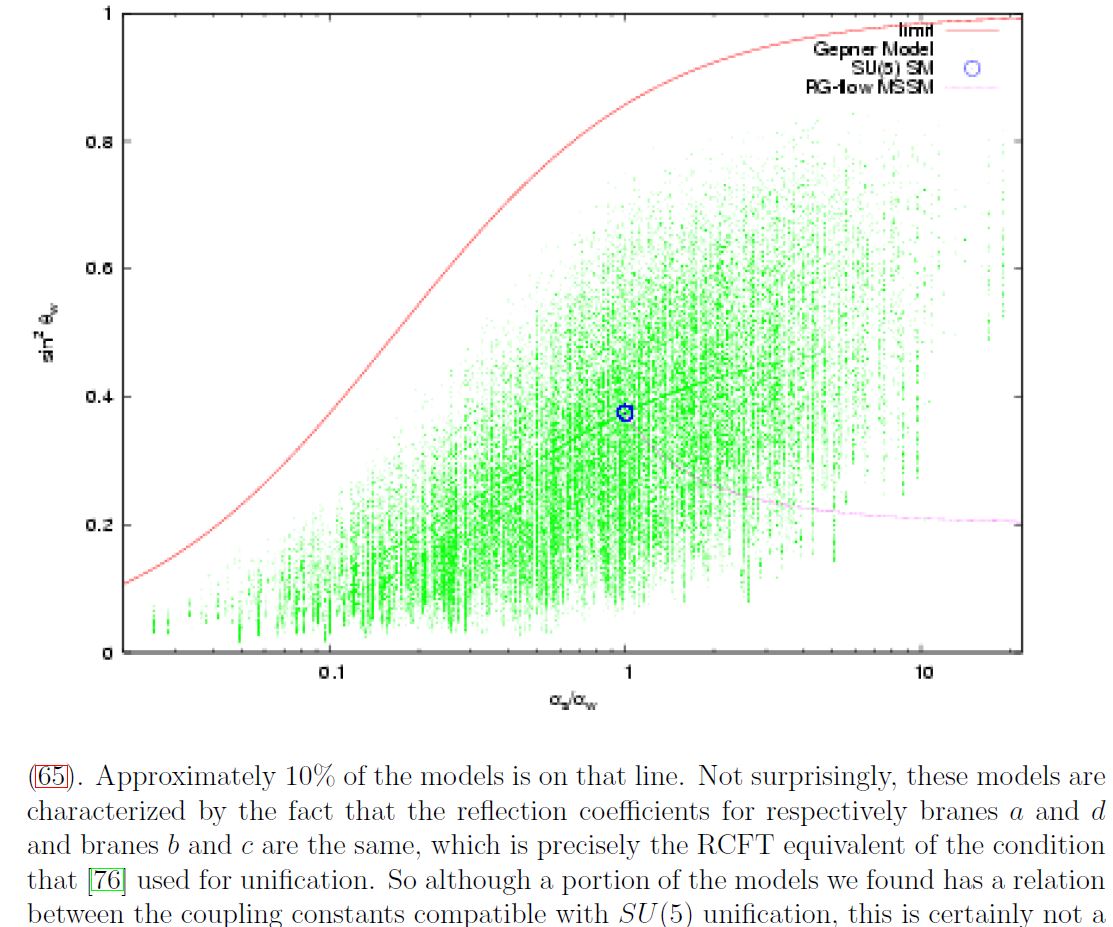
A plot of standard model-like coupling constants in a computer scan of Gepner model-KK-compactification of intersecting D-brane models according to Dijkstra-Huiszoon-Schellekens 04b.
The blue dot indicates the couplings in -GUT theory. The faint lines are NOT drawn by hand, but reflect increased density of Gepner models as seen by the computer scan.
Examples
General
brane intersections/bound states/wrapped branes/polarized branes
-
D-branes and anti D-branes form bound states by tachyon condensation, thought to imply the classification of D-brane charge by K-theory
-
intersecting D-branes/fuzzy funnels:
-
Dp-D(p+6) brane bound state
Intersecting D6-brane models
(…)
- S. Ishihara, H. Kataoka, Hikaru Sato, , , Type IIA Orientifolds, Phys. Rev. D60 (1999) 126005 (arXiv:hep-th/9908017)
(…)
Intersecting D4-brane models
Only D4-branes:
-
D. Bailin, G. V. Kraniotis, A. Love, Standard-like models from intersecting D4-branes, Phys. Lett. B530 (2002) 202-209 (arXiv:hep-th/0108131)
-
H. Kataoka, M. Shimojo, Chiral Models from Intersecting D4-/D5-branes, Progress of Theoretical Physics, Volume 107, Issue 6, June 2002, Pages 1291–1296 (arXiv:hep-th/0112247, doi:10.1143/PTP.107.1291)
-
D. Bailin, Standard-like models from D-branes, J Phys (2003) 60: 199 (arXiv:hep-th/0210227)
-
D. Bailin, G. V. Kraniotis, A. Love, New Standard-like Models from Intersecting D4-Branes, Phys. Lett. B547 (2002) 43-50 (arXiv:hep-th/0208103)
give the Witten-Sakai-Sugimoto model for holographic QCD

graphics grabbed from Erlich 09, section 1.1
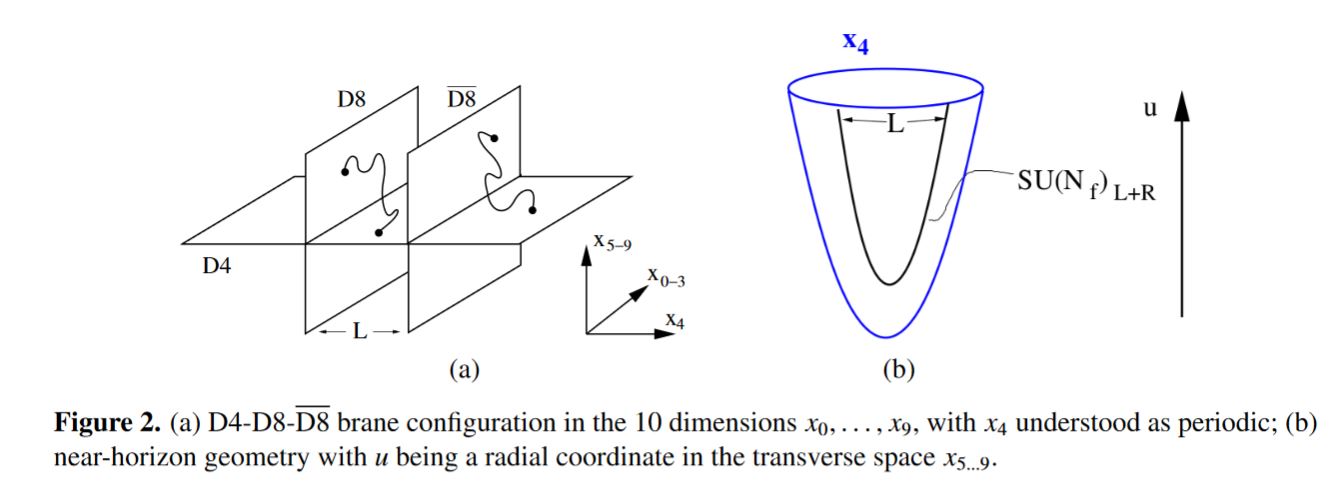
graphics grabbed from Rebhan 14
(…)
References
General
The bottom-up approach to intersecting D-brane model building was initiated in
- G. Aldazabal, Luis Ibáñez, F. Quevedo, Angel Uranga, D-Branes at Singularities : A Bottom-Up Approach to the String Embedding of the Standard Model, JHEP 0008:002 2000 (arXiv:hep-th/0005067)
The observation that chiral fermions appear when D6-branes intersect at an angle is due to
- Micha Berkooz, Michael Douglas, Robert Leigh, Branes Intersecting at Angles, Nucl. Phys. B480:265-278, 1996 (arXiv:hep-th/9606139)
development for toroidal orientifolds is due to
-
Stefan Forste, Gabriele Honecker, Ralph Schreyer, Orientifolds with branes at angles, JHEP 0106:004, 2001 (arXiv:hep-th/0105208)
-
Gabriele Honecker, Non-supersymmetric Orientifolds with D-branes at Angles, Fortsch.Phys. 50 (2002) 896-902 (arXiv:hep-th/0112174)
-
Gabriele Honecker, Non-supersymmetric orientifolds and chiral fermions from intersecting D6- and D8-branes, thesis 2002 (pdf)
Review includes
-
G. Aldazabal, Luis Ibáñez, F. Quevedo, On Realistic Brane Worlds from Type I Strings (arXiv:hep-ph/0005033)
-
Fernando Marchesano, Intersecting D-brane Models (arXiv:hep-th/0307252)
-
Ralph Blumenhagen, Mirjam Cvetic, Paul Langacker, Gary Shiu, Towards Realistic Intersecting D-Brane Models, Ann. Rev. Nucl. Part. Sci. 55:71-139, 2005 (arXiv:hep-th/0502005)
A textbook account is
- Luis Ibáñez, Angel Uranga, String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge 2012
Some chapters of which appear separately:
for D6-branes:
-
Angel Uranga, Model building in IIA: Intersecting brane worlds, 2012 (pdf, pdf)
for D7-branes:
-
Angel Uranga, Model building in type IIB string theory, 2012 (pdf)
-
Anshuman Maharana, Eran Palti, Models of Particle Physics from Type IIB String Theory and F-theory: A Review (arXiv:1212.0555)
Discussion of the Higgs mechanism in intersecting D-brane models:
-
Luis Ibáñez, Fernando Marchesano, R. Rabadan, section 7 of Getting just the Standard Model at Intersecting Branes, JHEP 0111:002, 2001 (arXiv:hep-th/0105155)
-
D. Cremades, Luis Ibáñez, Fernando Marchesano, Intersecting brane models of particle physics and the Higgs mechanism, JHEP, 0207, 022 2002 (arXiv:hep-th/0203160)
-
Arthur Hebecker, Alexander K. Knochel, Timo Weigand, The Higgs mass from a String-Theoretic Perspective, Nucl.Phys. B874 (2013) 1-35 (arXiv:1304.2767)
-
Manami Noumi Hashi, Hiroshi Isono, Toshifumi Noumi, Gary Shiu, Pablo Soler, Higgs Mechanism in Nonlocal Field Theories, JHEP08 (2018) 064 (arXiv:1805.02676)
See also
-
G. Aldazabal, S. Franco, Luis Ibáñez, R. Rabadan, A. M. Uranga, Chiral String Compactifications from Intersecting Branes, J.Math.Phys.42:3103-3126, 2001 (arXiv:hep-th/0011073)
-
Ralph Blumenhagen, Volker Braun, Boris Kors, Dieter Lüst, The Standard Model on the Quintic, Summary of Talks at SUSY02, 1st Intl. Conference on String Phenomenology in Oxford, Strings 2002 and 35th Ahrenshoop Symposium. (arXiv:hep-th/0210083)
-
Dieter Lüst, Intersecting Brane Worlds – A Path to the Standard Model?, Class. Quant. Grav.21 : S1399-1424, 2004 (arXiv:hep-th/0401156)
-
Ching-Ming Chen, Tianjun Li, Dimitri V. Nanopoulos, Standard-Like Model Building on Type II Orientifolds, Nucl.Phys.B732:224-242,2006 (arXiv:hep-th/0509059)
-
Angel Uranga, The standard model from D-branes in string theory, talk at Padova, January 2008 (pdf)
-
Matthew J. Dolan, Sven Krippendorf, Fernando Quevedo, Towards a Systematic Construction of Realistic D-brane Models on a del Pezzo Singularity, JHEP 1110 (2011) 024 (arXiv:1106.6039)
-
Yuta Hamada, Tatsuo Kobayashi, Shohei Uemura, Standard Model-like D-brane models and gauge couplings, Nuclear Physics B Volume 897, August 2015, Pages 563-582 (arXiv:1409.2740)
-
Jill Ecker, Gabriele Honecker, Wieland Staessens, D6-Brane Model Building on : MSSM-like and Left-Right Symmetric Models, Nuclear Physics B Volume 901, December 2015, Pages 139-215, (arXiv:1509.00048)
-
Jacob Bardzell, Kevin Federico, Danielle Smith, Timm Wrase?, On the absence of supergravity solutions for localized, intersecting sources [arXiv:2403.09873]
Intersection with O8-planes/D8-branes (M-theory on S1/G_HW times H/G_ADE) is discussed in
-
Amihay Hanany, Alberto Zaffaroni, Branes and Six Dimensional Supersymmetric Theories, Nucl.Phys. B529 (1998) 180-206 (arXiv:hep-th/9712145)
-
Amihay Hanany, Alberto Zaffaroni, Monopoles in String Theory, JHEP 9912 (1999) 014 (arXiv:hep-th/9911113)
-
E. Gorbatov, Vadim Kaplunovsky, Jacob Sonnenschein, Stefan Theisen, Shimon Yankielowicz, On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015 (2002) [arXiv:hep-th/0108135]
-
Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Futoshi Yagi, 6d SCFTs, 5d Dualities and Tao Web Diagrams (arXiv:1509.03300)
The landscape of models
On the landscape of intersecting D-brane models:
Computer scan of Gepner model-KK-compactifications of intersecting D-brane models:
-
T.P.T. Dijkstra, L. R. Huiszoon, Bert Schellekens, Chiral Supersymmetric Standard Model Spectra from Orientifolds of Gepner Models, Phys.Lett. B609 (2005) 408-417 (arXiv:hep-th/0403196)
-
T.P.T. Dijkstra, L. R. Huiszoon, Bert Schellekens, Supersymmetric Standard Model Spectra from RCFT orientifolds, Nucl.Phys.B710:3-57,2005 (arXiv:hep-th/0411129)
Computer scan of toroidal orbifold-KK compactifications is discussed in
-
Ralph Blumenhagen, Florian Gmeiner, Gabriele Honecker, Dieter Lüst, Timo Weigand, The Statistics of Supersymmetric D-brane Models, Nucl.Phys.B713:83-135, 2005 (arXiv:hep-th/0411173)
-
Florian Gmeiner, Ralph Blumenhagen, Gabriele Honecker, Dieter Lüst, Timo Weigand, One in a Billion: MSSM-like D-Brane Statistics, JHEP 0601:004, 2006 (arXiv:hep-th/0510170)
Detailed realistic models
Realistic Yukawa couplings and fermion masses in an MSSM Pati-Salam GUT model with 3 generations of fermions realized on intersecting D6-branes KK-compactified on a toroidal orbifold are claimed in
-
Ching-Ming Chen, Tianjun Li, Van Eric Mayes, Dimitri Nanopoulos, A Realistic World from Intersecting D6-Branes, Phys.Lett.B665:267-270, 2008 (arXiv:hep-th/0703280, doi:10.1016/j.physletb.2008.06.024)
-
Ching-Ming Chen, Tianjun Li, Van Eric Mayes, Dimitri Nanopoulos, Realistic Yukawa Textures and SUSY Spectra from Intersecting Branes, Phys.Rev.D77:125023, 2008 (arXiv:0711.0396)
-
Van Eric Mayes, All Fermion Masses and Mixings in an Intersecting D-brane World (arXiv:1902.00983)
-
Jordan Gemmill, Evan Howington, Van Eric Mayes, One String to Rule Them All: Neutrino Masses and Mixing Angles (arXiv:1907.07106)
-
Tianjun Li, Adeel Mansha, Rui Sun, Revisiting the Supersymmetric Pati-Salam Models from Intersecting D6-branes (arXiv:1910.04530)
-
Tianjun Li, Adeel Mansha, Rui Sun, Generalized Supersymmetric Pati-Salam Models from Intersecting D6-branes (arXiv:1912.11633)
Lift to M-theory
Lift of intersecting D-brane models to M-theory on G₂-manifolds with ADE-singularities is discussed in the following articles
-
Per Berglund, Andreas Brandhuber, Matter from -manifolds, Nucl.Phys. B641 (2002) 351-375 (arXiv:hep-th/0205184)
-
K. Behrndt, Gianguido Dall'Agata, Dieter Lüst, S. Mahapatra, Intersecting 6-branes from new 7-manifolds with holonomy, JHEP 0208:027 (2002) [arXiv:hep-th/0207117]
-
Jacob L. Bourjaily, Sam Espahbodi, Geometrically Engineerable Chiral Matter in M-Theory (arXiv:0804.1132)
Cosmology
Discussion for cosmology of intersecting D-brane models (ambient anti de Sitter spacetimes with the conformal intersecting branes at the asymptotic boundary) includes the following (see also at Randall-Sundrum model):
-
Igor Klebanov, Matthew Strassler, Supergravity and a Confining Gauge Theory: Duality Cascades and -Resolution of Naked Singularities, JHEP 0008:052, 2000 (arXiv:hep-th/0007191)
-
Igor Klebanov, Edward Witten, Superconformal Field Theory on Threebranes at a Calabi-Yau Singularity, Nucl.Phys.B536:199-218, 1998 (arXiv:hep-th/9807080)
-
Luis Anchordoqui, Jose Edelstein, Carlos Nunez, Santiago Perez Bergliaffa, Martin Schvellinger, Marta Trobo, Fabio Zyserman, Brane Worlds, String Cosmology, and AdS/CFT, Phys. Rev. D64:084027, 2001 (arXiv:hep-th/0106127)
-
Nemanja Kaloper, Origami World, JHEP 0405 (2004) 061 (arXiv:hep-th/0403208)
-
Angel Uranga, section 18 of TASI lectures on String Compactification, Model Building, and Fluxes, 2005 (pdf, cern:933469)
-
Antonino Flachi, Masato Minamitsuji, Field localization on a brane intersection in anti-de Sitter spacetime, Phys.Rev.D79:104021, 2009 (arXiv:0903.0133)
-
Jiro Soda, AdS/CFT on the brane, Lect.Notes Phys.828:235-270, 2011 (arXiv:1001.1011)
-
Gianluca Grignani, Troels Harmark, Andrea Marini, Marta Orselli, The Born-Infeld/Gravity Correspondence, Phys. Rev. D 94, 066009 (2016) (arXiv:1602.01640)
Survey is in
-
Antonio Padilla, Braneworld Cosmology and Holography (arxiv:hep-th/0210217)
-
Shunsuke Teraguchi, around slide 21 of: String theory and its relation to particle physics, 2007 (pdf)
Discussion of 4d de Sitter spacetime cosmology models on brane worlds in AdS bulk spacetimes:
-
Souvik Banerjee, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Marjorie Schillo, Emergent de Sitter cosmology from decaying AdS (arXiv:1807.01570)
-
Souvik Banerjee, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Marjorie Schillo, de Sitter Cosmology on an expanding bubble (arXiv:1907.04268)
Experimental tests
Discussion of observational/experimental test of brane world models:
by analysis of the event horizon of the black hole in the center of the galaxy Messier 87:
- Indrani Banerjee, Sumanta Chakraborty, Soumitra SenGupta, Silhouette of M87: A new window to peek into the world of hidden dimensions (arXiv:1909.09385)
Last revised on August 15, 2025 at 05:20:01. See the history of this page for a list of all contributions to it.