nLab quantum computation

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Redirected from "NISQ".
Contents

Context

Computation

constructive mathematics, realizability, computability

intuitionistic mathematics

propositions as types, proofs as programs, computational trinitarianism

Constructive mathematics

Realizability

Computability

Quantum systems

quantum logic


quantum physics


quantum probability theory – observables and states


quantum information


quantum computation

qbit

quantum algorithms:


quantum sensing


quantum communication

Contents

Idea

General

Quantum computation is computation in terms of quantum information theory, possibly implemented on quantum computers, hence on physical systems for which phenomena of quantum mechanics are not negligible: quantum systems such as consisting of fundamental particles like photons or electrons but also often of quantum-quasiparticles such as Cooper pairs in superconductors.

In terms of the computational trilogy, quantum computation is the computation corresponding to (some kind of) quantum logic/(dependent) linear type theory.

To the extent that quantum computation involves quantum measurement (generally to read out results, but often also as a kind of quantum logic gate in its own right) it is a form of nondeterministic computation, due to the intrinsic stochastic nature of the quantum state collapse during quantum measurement.

However, away from quantum measurement, quantum gates are understood to implement unitary operators on a given Hilbert space of quantum states (fundamentally due to the unitary nature of time-evolution as given by the Schrödinger equation), for which quantum computation is hence not only deterministic but in fact a form of reversible computation. This relates to its susceptibility to noise and the practical need for quantum error correction and/or topological quantum stabilization.

Specifically, topological quantum computation is (or is meant to be) quantum computation implemented on physical systems governed by topological quantum field theory, such as Chern-Simons theory, thought to describe for instance anyon defects in topologically ordered gapped ground states of quantum materials in topological phases of matter.

Classical control, quantum data

Any practical quantum computer will be classically controlled (an idea that may be traced back to Knill 96, Ömer 03, for more pronounced discussion see Devitt 14).

(from Miszczak 11, Fig. 9)

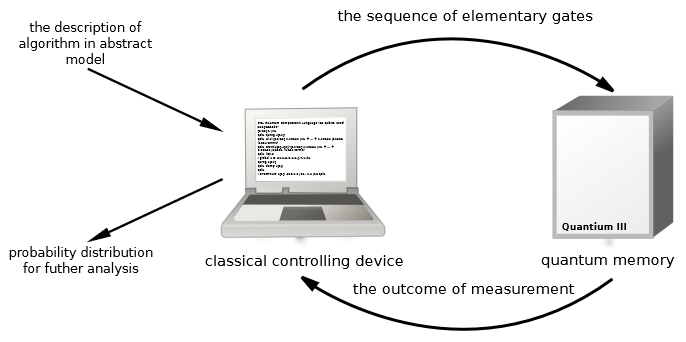
Already for presently available NISQ machines, classically-parameterized quantum systems have been considered in contexts such as quantum machine learning [BLSF 19]:

(from BLSF 19, Fig. 1)

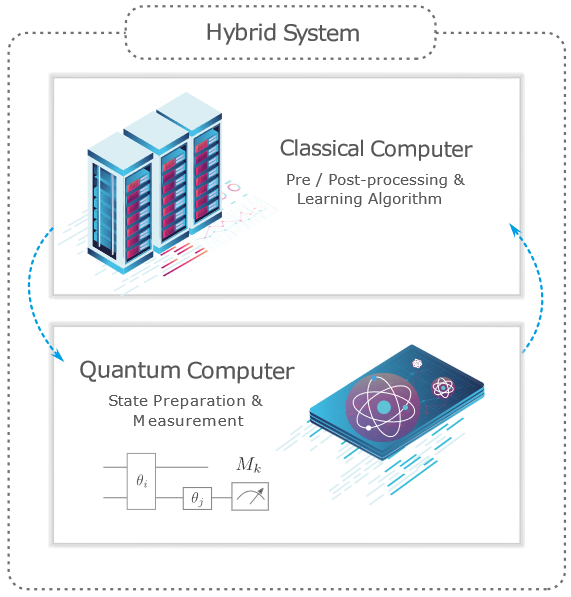
Here the classical control itself is generally conditioned on quantum measurement-outcomes — notably syndrome-measurements for quantum error correction — available only during runtime, a mechanism that in the quantum programming languages-community (Quipper) has come to be called “dynamic lifting”:

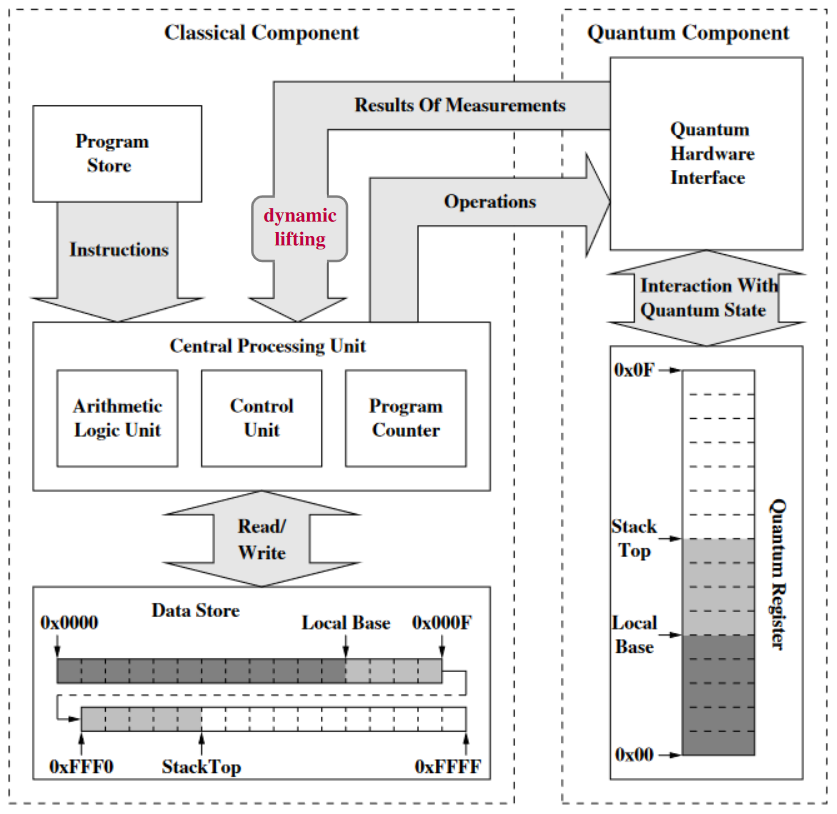
(SQRAM model adapted from Nagarajan, Papanikolaou and Williams 2007, Fig 1)

\,

[Devitt 14, p. 2:]

Irrespective of the actual quantum code chosen to protect a quantum computer, it is well known that operating such as system requires extensive classical control infrastructure. This is not simply related to the control of the physical device hardware needed to operate a qubit (lasers, signal generators etc…), but it is also required to decode error correction information produced by the computer.

[KESWDSC 23, p. 2:]

Apart from the requirements on the quantum hardware, the successful execution of QEC codes depends on the classical control system. The classical control system is responsible for all classical aspects of quantum computing and includes executing the quantum control and measurement signals, acquiring the readout signals, andperforming classical processing operations, all in a synchronized manner. In QEC, the control system is also responsible for mapping the local physical measurements into logical measurement results or logical Pauli frame updates through an algorithmic procedure called decoding. To reach useful quantum computation with QEC, i.e., perform faultolerant non-Clifford gates, the control unit is required to perform quantum gates that depend on the decoding output. Moreover, to prevent a diverging classical calculation latency, it is crucial for the control system to close a tight loop, with ultra-low latency, from the physical quantum measurement through the classical decoding procedure to a conditional feed-forward quantum operation. Thus, the success of fault-tolerant quantum computation depends on minimizing the QEC feed-forward latency.

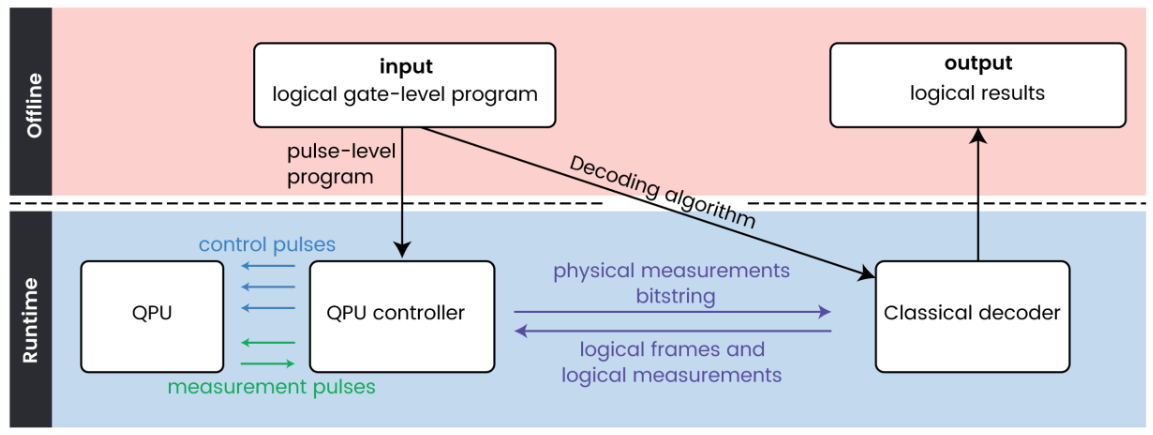
(QECCP schematics fom KESWDSC 23, Fig. 2)

For more on technical details of classical control requirements see also CRKAW 24.

Generally, see the list of references below.

Quantum languages and quantum circuits

A natural way to understand (via computational trilogism) quantum programming languages is as linear logic/linear type theory (Pratt 92, for more see at quantum logic) with categorical semantics in non-cartesian symmetric monoidal categories (Abramsky & Coecke 04, Abramsky & Duncan 05, Duncan 06, Lago-Faffian 12). .

The corresponding string diagrams are known as quantum circuit diagrams.

In fact, languages for classically controlled quantum computation should be based on dependent linear type theory (Vakar 14, Vakar 15, Vakar 17, Sec. 3, Lundfall 17, Lundfall 18, following Schreiber 14) with categorical semantics in indexed monoidal categories:

classical controlquantum data
intuitionistic typesdependent linear types

This idea of classically controlled quantum programming via dependent linear type theory has been implemented in QML and in Quipper in FKS 20, FKRS 20.

Examples

References

General

The idea of quantum computation was first expressed in:

  • Yuri I. Manin, Introduction to: Computable and Uncomputable, Sov. Radio (1980) [Russian original: pdf], Enlish translation on p. 69-77 of Mathematics as Metaphor: Selected essays of Yuri I. Manin, Collected Works 20, AMS (2007) [ISBN:978-0-8218-4331-4]

    Perhaps, for a better understanding of [molecular biology], we need a mathematical theory of quantum automata.

  • Paul Benioff, The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines, J Stat Phys 22, 563–591 (1980) [doi:10.1007/BF01011339]

  • Paul Benioff, Quantum Mechanical Models of Turing Machines That Dissipate No Energy, Phys. Rev. Lett. 48 1581 (1982) [doi:10.1103/PhysRevLett.48.1581]

  • Richard Feynman, Simulating physics with computers, Int J Theor Phys 21 (1982) 467–488 [doi:10.1007/BF02650179]

    “because nature isn’t classical, dammit, if you want to make a simulation of nature, you’d better make it quantum mechanical”

First ideas of a quantum Turing machine:

The notion of (controlled) quantum logic gates and quantum circuits was first made explicit in:

The terminology q-bit goes back to:

The potential practical relevance of quantum computation was highlighted early on via toy examples

such as the Deutsch-Jozsa algorithm:

and became widely appreciated in 1996/1997 with the discovery of several practically interesting algorithms exhibiting “quantum supremacy”, such as:

in quantum chemistry

in search algorithms (Grover's algorithm)

and in (quantum) cryptography (Shor's algorithm)

The first realistic proposal for actually building a quantum gate (namely on trapped ions):

Quantum computation became widely thought to be not just a theoretical but a plausible practical possibility with the theoretical understanding of quantum error correction (which however remains to be implemented scalably):

Early review:

Monograph on experimental realizations of quantum gates/quantum computers:

  • Chen, Church, Englert, Henkel, Rohwedder, Scully, Zubairy: Quantum Computing Devices – Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]

Review of quantum algorithms:

An alternative/parallel approach to avoiding errors due to decoherence is topological quantum computation, see there for references.

Influential list of criteria necessary for physical realization of quantum computation:

Simple quantum computers have been realized (first with NMR technology, see references below, then with superconductor technology, see references further below) and have been argued to demonstrate quantum supremacy (see there for references) but existing machines remain “noisy and intermediate scale” (see the references below).

Textbook accounts on quantum computation:

Introducing the notion of quantum supremacy and highlighting its relation to quantum entanglement:

  • John Preskill: Quantum computing and the entanglement frontier: pp. 63-80 in: The Theory of the Quantum World – Proceedings of the 25th Solvay Conference on Physics, World Scientific (2013) [arXiv:1203.5813, doi:10.1142/8674, slides: pdf]

Further introduction and survey:

On “continuous variable” analog quantum computation:

See also:

Experimental demonstration of “quantum supremacy” (“quantum advantage”):

Review:

Potential relation to the Unruh effect?:

  • Eric W. Aspling, John A. Marohn, Michael J. Lawler, Design Constraints for Unruh-DeWitt Quantum Computers [arXiv:2210.12552]

Quantum programming languages

The first proposal towards formalizing quantum programming languages was:

and early formalization via quantum lambda-calculus invoking linear logic/linear types (cf. Pratt 1992 etc.):

[Selinger (2016):] When the QPL workshop series was first founded, it was called “Quantum Programming Languages”. One year I wasn’t participating, and while I wasn’t looking they changed the name to “Quantum Physics and Logic” — same acronym!

Back in those days in the early 21st century we were actually trying to do programming languages for quantum computing [[Selinger & Valiron 2004]], but the sad thing is: In those days nobody really cared. [...][...]

Now it’s 15 years later and several of these parameters have changed: There has been a renewed interest, from government agencies and also from companies who are actually building quantum computers. [...][...].

So now people are working on quantum programming languages again.

Exposition of the general idea of quantum programming languages for classically controlled quantum computation with an eye towards the Quipper-language:

On quantum programming languages (programming languages for quantum computation):

General:

See also:

Surveys of existing languages:

  • Simon Gay, Quantum programming languages: Survey and bibliography, Mathematical Structures in Computer Science16(2006) (doi:10.1017/S0960129506005378, pdf)

  • Sunita Garhwal, Maryam Ghorani , Amir Ahmad, Quantum Programming Language: A Systematic Review of Research Topic and Top Cited Languages, Arch Computat Methods Eng 28, 289–310 (2021) (doi:10.1007/s11831-019-09372-6)

  • B. Heim et al., Quantum programming languages, Nat Rev Phys 2 (2020) 709–722 [[doi:10.1038/s42254-020-00245-7]]

Quantum programming via quantum logic understood as linear type theory interpreted in symmetric monoidal categories:

The corresponding string diagrams are known in quantum computation as quantum circuit diagrams:

Typed\;functional programming languages for quantum computation:

QPL:

QML:

quantum IO monad:

Quipper:

QWIRE:

CoqQ:


On Q Sharp:

  • Kartik Singhal, Kesha Hietala, Sarah Marshall, Robert Rand, Q# as a Quantum Algorithmic Language, Proceedings of Quantum Physics and Logic (2022) [[arXiv:2206.03532]]

On classically controlled quantum computation:

Quantum programming via dependent linear type theory/indexed monoidal (∞,1)-categories:

specifically with Quipper:

See also QS.

On quantum software engineering:

On software verification:

with QWIRE:

for Quipper with QPMC:

  • Linda Anticoli, Carla Piazza, Leonardo Taglialegne, Paolo Zuliani, Towards Quantum Programs Verification: From Quipper Circuits to QPMC, In: Devitt S., Lanese I. (eds.) Reversible Computation. RC 2016, Lecture Notes in Computer Science 9720 Springer (2016) [[arXiv:1708.06312, doi:10.1007/978-3-319-40578-0_16]]

with CoqQ: Ying et al. (2022)

Classically controlled quantum computing

Theory of classically controlled quantum computing and parameterized quantum circuits:

  • Emanuel Knill, Conventions for quantum pseudocode, Los Alamos Technical Report (1996) [LA-UR-96-2724, doi:10.2172/366453, pdf]

  • Bernhard Ömer, Structured Quantum Programming, 2003/2009 (pdf)

  • Simon Perdrix, Philippe Jorrand, Classically-Controlled Quantum Computation, Math. Struct. in Comp. Science, 16:601-620, 2006 (arXiv:quant-ph/0407008)

  • Rajagopal Nagarajan, Nikolaos Papanikolaou, David Williams, Simulating and Compiling Code for the Sequential Quantum Random Access Machine, Electronic Notes in Theoretical Computer Science Volume 170, 6 March 2007, Pages 101-124 (doi:10.1016/j.entcs.2006.12.014)

  • Jarosław Adam Miszczak, Models of quantum computation and quantum programming languages, Bull. Pol. Acad. Sci.-Tech. Sci., Vol. 59, No. 3 (2011), pp. 305-324 (arXiv:1012.6035)

  • Simon J. Devitt, Classical Control of Large-Scale Quantum Computers, In: S. Yamashita, S. Minato (eds.) Reversible Computation Lecture Notes in Computer Science 8507, Springer (2014) [arXiv:1405.4943, doi:10.1007/978-3-319-08494-7_3]

  • Jarrod R McClean, Jonathan Romero, Ryan Babbush and Alán Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, New Journal of Physics, Volume 18, February 2016 (doi:10.1088/1367-2630/18/2/023023)

  • Murray Thom (D-Wave), Three Truths and the Advent of Hybrid Quantum Computing (Jun 25, 2019)

  • Yaniv Kurman, Lior Ella, Ramon Szmuk, Oded Wertheim, Benedikt Dorschner, Sam Stanwyck, Yonatan Cohen: Control Requirements and Benchmarks for Quantum Error Correction [arXiv:2311.07121]

  • Daan Camps, Ermal Rrapaj, Katherine Klymko, Brian Austin, Nicholas J. Wright: Evaluation of the Classical Hardware Requirements for Large-Scale Quantum Computations, ISC High Performance 2024 Research Paper Proceedings (39th International Conference), Hamburg, Germany (2024) 1-12 [doi:10.23919/ISC.2024.10528937]

Application of classically controlled quantum computation:

  • Isaac H. Kim, Brian Swingle, Robust entanglement renormalization on a noisy quantum computer (arXiv:1711.07500)

    (in terms of holographic tensor network states)

  • Sukin Sim, Peter D. Johnson, Alan Aspuru-Guzik, Expressibility and entangling capability of parameterized quantum circuits for hybrid quantum-classical algorithms, Adv. Quantum Technol. 2 (2019) 1900070 (arXiv:1905.10876)

  • Mateusz Ostaszewski, Edward Grant, Marcello Benedetti, Structure optimization for parameterized quantum circuits, Quantum 5, 391 (2021) (arXiv:1905.09692)

  • Ruslan Shaydulin et al., A Hybrid Approach for Solving Optimization Problems on Small Quantum Computers (doi:10.1109/MC.2019.2908942)

  • Eneko Osaba, Esther Villar-Rodriguez, Izaskun Oregi, Aitor Moreno-Fernandez-de-Leceta, Focusing on the Hybrid Quantum Computing – Tabu Search Algorithm: new results on the Asymmetric Salesman Problem (arXiv:2102.05919)

in particular in quantum machine learning:

  • Marcello Benedetti, Erika Lloyd, Stefan Sack, Mattia Fiorentini, Parameterized quantum circuits as machine learning models, Quantum Science and Technology 4 043001 (2019) [arXiv:1906.07682]

  • D. Zhu et al. Training of quantum circuits on a hybrid quantum computer, Science Advances, 18 Oct 2019: Vol. 5, no. 10, eaaw9918 (doi: 10.1126/sciadv.aaw9918)

  • Andrea Mari, Thomas R. Bromley, Josh Izaac, Maria Schuld, Nathan Killoran, Transfer learning in hybrid classical-quantum neural networks, Quantum 4, 340 (2020) (arXiv:1912.08278)

  • Thomas Hubregtsen, Josef Pichlmeier, Patrick Stecher, Koen Bertels, Evaluation of Parameterized Quantum Circuits: on the relation between classification accuracy, expressibility and entangling capability, Quantum Machine Intelligence volume 3, Article number: 9 (2021) (arXiv:2003.09887, doi:10.1007/s42484-021-00038-w)

  • TensorFlow.org (Google), Hybrid quantum classical models

Noisy intermediate-scale quantum (NISQ) computing

The origin of the notion:

On the limitations of (quantum error-corrected) NISQ machines in achieving any quantum advantage:

  • Subhash Kak: Prospects for Quantum Computing, talk at CIFAR Nanotechnology program meeting, Halifax (November 2008) [arXiv:0902.4884]

  • M. I. Dyakonov: Prospects for quantum computing: extremely doubtful, Int. J. of Modern Physics: Conf. Series 33 (2014) 1460357 [arXiv:1401.3629, doi:10.1142/S2010194514603573]

  • Daniel Koch, Brett Martin, Saahil Patel, Laura Wessing, and Paul M. Alsing, Demonstrating NISQ era challenges in algorithm design on IBM’s 20 qubit quantum computer, AIP Advances 10 095101 (2020) [doi:10.1063/5.0015526]

  • Frank Leymann, Johanna Barzen, The bitter truth about gate-based quantum algorithms in the NISQ era, Quantum Sci. Technol. 5 044007 (2020) [doi:10.1088/2058-9565/abae7d]

  • Olivier Ezratty, Where are we heading with NISQ? [arXiv:2305.09518, InSpire:2660378]

    “no one has yet successfully implemented a use case matching the original definition of the NISQ regime.”

    “Totally outside the NISQ relevant algorithms class are integer and discrete log factoring algorithms [Shor's algorithm], oracle based search algorithms [Grover's algorithm], and all algorithms relying on a quantum Fourier transform”

    “most NISQ experiments have been run with fewer than 30 qubits and should therefore better be labelled as “pre-NISQ”. While they are elegant proofs of concepts, they do not yet demonstrate any speed up over classical computing”

  • Olivier Ezratty, Where are we heading with NISQ?, blog post (2023) [web, pdf]

    NISQ is not at all ready for prime time quantum computing despite all the fuss about “quantum computing being business ready”. Not only have we not yet reached any quantum computing advantage, but in many cases, even if it worked, the most common NISQ algorithms using a variational approach, have prohibitively long execution times particularly in the promising chemical simulations domain.

  • Jonathan Wei Zhong Lau, Kian Hwee Lim, Harshank Shrotriya, Leong Chuan Kwek, NISQ computing: where are we and where do we go?, AAPPS Bull. 32 27 (2022) [doi:10.1007/s43673-022-00058-z]

    However, quantum computers are still far from achieving all that they have promised. While early-stage quantum computers have been developed, the problems of noisy calculations and scalability of quantum computers still plague the field. As opposed to the far future, where quantum computers can be as big as we wish them to be and are capable of performing fully controllable operations (termed as the fault-tolerant era), we are currently working in the Noisy Intermediate-Scale Quantum (NISQ) era, which is an operational definition that implies that the quantum computers available to us now are subject to substantial error rates and they are constrained in size (in terms of the number of qubits). While it is already a scientific achievement to get to this stage, such quantum computers are still incapable of showing any significant advantages over classical computers. As such, some people in the community have already expressed fear that there will be a ‘Quantum winter’, or a scenario where quantum computing devices remain noisy and are unable to scale up in terms of qubit size, preventing us from ever achieving a meaningful advantage over classical computers.

  • John Preskill, Crossing the Quantum Chasm: From NISQ to Fault Tolerance, talk at Q2B 2023 Silicon Valley (2023) [pdf, pdf]

    “there is no proposed application of NISQ computing with commercial value for which quantum advantage has been demonstrated”

    “Nor are there persuasive theoretical arguments indicating that commercially viable applications will be found that do not use quantum error-correcting codes and fault-tolerant quantum computing.”

  • Torsten Hoefler, Thomas Haener, Matthias Troyer, Disentangling Hype from Practicality: On Realistically Achieving Quantum Advantage, Communications of the ACM 66 5 (May 2023) 82-87 [arXiv:2307.00523, acm pdf, doi:10.1145/3571725]

    “A large range of problem areas with quadratic quantum speedups, such as many current machine learning training approaches, accelerating drug design and protein folding with Grover’s algorithm, speeding up Monte Carlo simulations through quantum walks, as well as more traditional scientific computing simulations including the solution of many non-linear systems of equations, such as fluid dynamics in the turbulent regime, weather, and climate simulations will not achieve quantum advantage with current quantum algorithms in the foreseeable future.”

  • Edd Gent: Quantum Computing’s Hard, Cold Reality Check, IEEE Spectrum (Dec. 2023) [webpage]

On the resulting drop in investment:

More optimistic outlook:

More concerned outlook:

>

  • DARPA: Quantum Benchmarjing Initiative

    “to determine if it’s possible to build an industrially useful quantum computer much faster than conventional predictions. Specifically, QBI is designed to rigorously verify and validate if any quantum computing approach can achieve utility-scale operation — meaning its computational value exceeds its cost — by the year 2033.”

    The accompanying video says at 1:25:

    “If it turns out, as a lot of us suspect, that that’s really not possible, and it really won’t do something useful, or there isn’t a path, we need to know that, too.”

Quantum programming via monads

Discussion of aspects of quantum programming in terms of monads in functional programming are in

As linear logic

Discussion of quantum computation as the internal linear logic/linear type theory of compact closed categories is in

An exposition along these lines is in

  • John Baez, Mike Stay, Physics, topology, logic and computation: a rosetta stone, arxiv/0903.0340; in “New Structures for Physics”, ed. Bob Coecke, Lecture Notes in Physics 813, Springer, Berlin, 2011, pp. 95-174

Quantum information theory via String diagrams

General

The observation that a natural language for quantum information theory and quantum computation, specifically for quantum circuit diagrams, is that of string diagrams in †-compact categories (see quantum information theory via dagger-compact categories):

On the relation to quantum logic/linear logic:

Early exposition with introduction to monoidal category theory:

Review in contrast to quantum logic:

and with emphasis on quantum computation:

Generalization to quantum operations on mixed states (completely positive maps of density matrices):

Textbook accounts (with background on relevant monoidal category theory):

Measurement & Classical structures

Formalization of quantum measurement via Frobenius algebra-structures (“classical structures”):

and the evolution of the “classical structures”-monad into the “spider”-diagrams (terminology for special Frobenius normal form, originating in Coecke & Paquette 2008, p. 6, Coecke & Duncan 2008, Thm. 1) of the ZX-calculus:

ZX-Calculus

Evolution of the “classical structures”-Frobenius algebra (above) into the “spider”-ingredient of the ZX-calculus for specific control of quantum circuit-diagrams:

Relating the ZX-calculus to braided fusion categories for anyon braiding:

Topological quantum computing

topological quantum computation is discussed in

Relation to tensor networks

Relation to tensor networks, specifically matrix product states:

  • Yiqing Zhou, E. Miles Stoudenmire, Xavier Waintal, What limits the simulation of quantum computers?, arXiv:2002.07730

Spin resonance qbits

The idea of spin resonance qbits, i.e. of qbits realized on quantum mechanical spinors (e.g. electron-spin or nucleus-spin) and manipulated via spin resonance:

The very first proof-of-principle quantum computations were made with nuclear magnetic resonance-technology:

See also:

  • Lieven Vandersypen, Mark Eriksson: Quantum computing with semiconductor spins, Physics Today 72 8 (2019) 38 [doi:10.1063/PT.3.4270]

Monograph:

  • Chen, Church, Englert, Henkel, Rohwedder, Scully, Zubairy, section 10 of: Quantum Computing Devices – Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]

Exposition, review and outlook:

  • Raymond Laflamme, Emanuel Knill, et al., Introduction to NMR Quantum Information Processing, Proceedings of the International School of Physics “Enrico Fermi” 148 Experimental Quantum Computation and Information [arXiv:quant-ph/0207172]

  • Asif Equbal, Molecular spin qubits for future quantum technology, talk at CQTS (Nov 2022) [slides: pdf, video: rec]

  • Jonathan A. Jones, Controlling NMR spin systems for quantum computation, Spectroscopy 140–141 (2024) 49-85 [doi:10.1016/j.pnmrs.2024.02.002, arXiv:2402.01308]

    “Nuclear magnetic resonance is arguably both the best available quantum technology for implementing simple quantum computing experiments and the worst technology for building large scale quantum computers that has ever been seriously put forward. After a few years of rapid growth, leading to an implementation of Shor’s quantum factoring algorithm in a seven-spin system, the field started to reach its natural limits and further progress became challenging. […] the user friendliness of NMR implementations means that they remain popular for proof-of-principle demonstrations of simple quantum information protocols.”

See also:

More on implementation of quantum logic gates on qbits realized on nucleon-spin, via pulse protocols in NMR-technology:

  • Price, Somaroo, Tseng, Gore, Fahmy,, Havel, Cory: Construction and Implementation of NMR Quantum Logic Gates for Two Spin Systems, Journal of Magnetic Resonance 140 2 (1999) 371-378 [[doi;10.1006/jmre.1999.1851]]

and analogously on electron-spin:

  • M. Yu. Volkov and K. M. Salikhov, Pulse Protocols for Quantum Computing with Electron Spins as Qubits, Appl Magn Reson 41 (2011) 145–154 [[doi:10.1007/s00723-011-0297-2]]

For references on spin resonance qbits realized on a nitrogen-vacancy center in diamond, see there.

There exist toy desktop quantum computers for educational purposes, operating on a couple of nuclear magnetic resonance qbits at room temperature :

Superconducting qbits

On realizing qbits and quantum gates (hence quantum computation) via quantum states of magnetic flux through (Josephson junctions in) superconductors, manipulated via electromagnetic pulses:

Monograph:

  • Chen, Church, Englert, Henkel, Rohwedder, Scully, Zubairy, section 9 of: Quantum Computing Devices Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]

Fine detail of the pulse control:

  • M. Werninghaus, D. J. Egger, F. Roy, S. Machnes, F. K. Wilhelm, S. Filipp: Leakage reduction in fast superconducting qubit gates via optimal control, npj Quantum Information 7 14 (2021) [[doi:10.1038/s41534-020-00346-2]]

  • M. Carroll, S. Rosenblatt, P. Jurcevic, I. Lauer & A. Kandala. Dynamics of superconducting qubit relaxation times, npj Quantum Information 8 132 (2022) [[doi:10.1038/s41534-022-00643-y]]

  • Elisha Siddiqui Matekole, Yao-Lung L. Fang, Meifeng Lin, Methods and Results for Quantum Optimal Pulse Control on Superconducting Qubit Systems, 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (2022) [[arXiv:2202.03260, doi:10.1109/IPDPSW55747.2022.00102]]

Corrections due to quasiparticle-excitations:

Photonic qbits

Realization in photonics:

  • Han-Shen Zhong et al. Quantum computational advantage using photons, Science 370, n. 6523 (2020) 1460-1463 doi

Commercial quantum computers

Since 2019, NISQ quantum computers can be accessed through cloud services:

There exist toy desktop quantum computers for educational purposes, operating on a couple of nuclear magnetic resonance qbits at room temperature :

category: computer science, physics

Last revised on December 18, 2024 at 11:47:34. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (137 revisions) Cite Print Source