nLab configuration space of points
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
- Idea
- Definition
- Properties
- Basic properties
- Ordered unlabeled configurations from unordered labeled configurations
- Cohomotopy charge map
- Relation to iterated loop spaces of iterated suspensions
- Relation to classifying space of the symmetric group
- Relation to James construction
- In twisted Cohomotopy
- Rational maps to complex projective space
- Knizhnik-Zamolodchicov connection
- Action by little -disk operad and by Goodwillie derivatives
- Homology and stabilization in homology
- Gauss-Manin connections
- Rational homotopy type
- Relation to weight systems, chord diagrams and Vassiliev invariants
- Berry-Robbins and Atiyah-Sutcliffe construction
- Occurrences and Applications
- Compactification
- Stable splitting of mapping spaces
- Correlators as differential forms on configuration spaces
- Related concepts
- References
- General
- Cohomotopy charge map
- Stable splitting of mapping spaces
- In Goodwillie-calculus
- Compactification
- Homology and cohomology
- Homotopy
- Rational homotopy type
- Cohomology modeled by graph complexes
- Loop spaces of configuration spaces of points
- Graph configuration spaces
- Configurations in general position
- In quantum (field) theory
- Braid representations via twisted cohomology of configuration spaces
- As moduli of Dp-D(p+4)-brane bound states:
Idea
In mathematics, the term “configuration space” of a topological space typically refers by default to the topological space of pairwise distinct points in , also called Fadell's configuration space, for emphasis.
In principle many other kinds of configurations and the spaces these form may be referred to by “configuration space”, notably in physics the usage is in a broader sense, see at configuration space (physics).
Definition
Several variants of configuration spaces of points are of interest. They differ in whether
-
points are linearly ordered or not;
-
points are labeled in some labelling space;
-
points vanish on some subspace or if their labels are in some subspace.
Here are some of these variant definitions:
Ordered unlabeled points
Definition
(ordered unlabeled configurations of a fixed number of points)
Let be a closed smooth manifold. For write
for the complement of the fat diagonal inside the -fold Cartesian product of with itself.
This is the space of ordered but otherwise unlabeled configurations of points_ in .
Unordered unlabeled points
Definition
(unordered unlabeled configurations of a fixed number of points)
Let be a closed smooth manifold, For write
for the quotient space of the ordered configuration space (Def. ) by the evident action of the symmetric group via permutation of the ordering of the points.
This is the space of unordered and unlabeled configurations of points_ in .
We write
for the unordered unlabeled configuration space of any finite number of points, being the disjoint union of these spaces (1) over all natural numbers .
Remark
(monoid-structure on configuration space of points)
For a Euclidean spaces the configuration space of points (2) carries the structure of a topological monoid with product operation being the disjoint union of point configurations, after a suitable shrinking to put them next to each other (Segal 73, p. 1-2).
For emphasis, we write for the delooping (“classifying space”) with respect to this topological monoid-structure. The corresponding based loop space is then the group completion of the configuration space, with respect to disjoint union of points:
Remark
The configuration space of unordered unlabeled configurations of points (Def. ) is naturally a topological subspace of the space of finite subsets of cardinality
Proposition
Let be an non-empty regular topological space and .
Then the injection (4)
of the unordered configuration space of n points of (Def. ) into the quotient space of the space of finite subsets of cardinality by its subspace of subsets of cardinality is an open subspace-inclusion.
Moreover, if is compact, then so is and the inclusion (5) exhibits the one-point compactification of the configuration space:
(Handel 00, Prop. 2.23, see also Félix-Tanré 10)
Unordered labeled points
Definition
For a smooth manifold and , the space of unordered configurations of points in with labels in is
For , consider the k-sphere as a pointed topological space, with the base point regarded as the “vanishing label”.
Definition
(unordered labeled configurations vanishing with vanishing label)
For a smooth manifold and , the space of unordered configurations of points in with labels in and vanishing at vanishing label value is the quotient space
of the disjoint union of all unordered labeled -point configuration spaces (6) by the equivalence relation which regards points with vanishing label as absent.
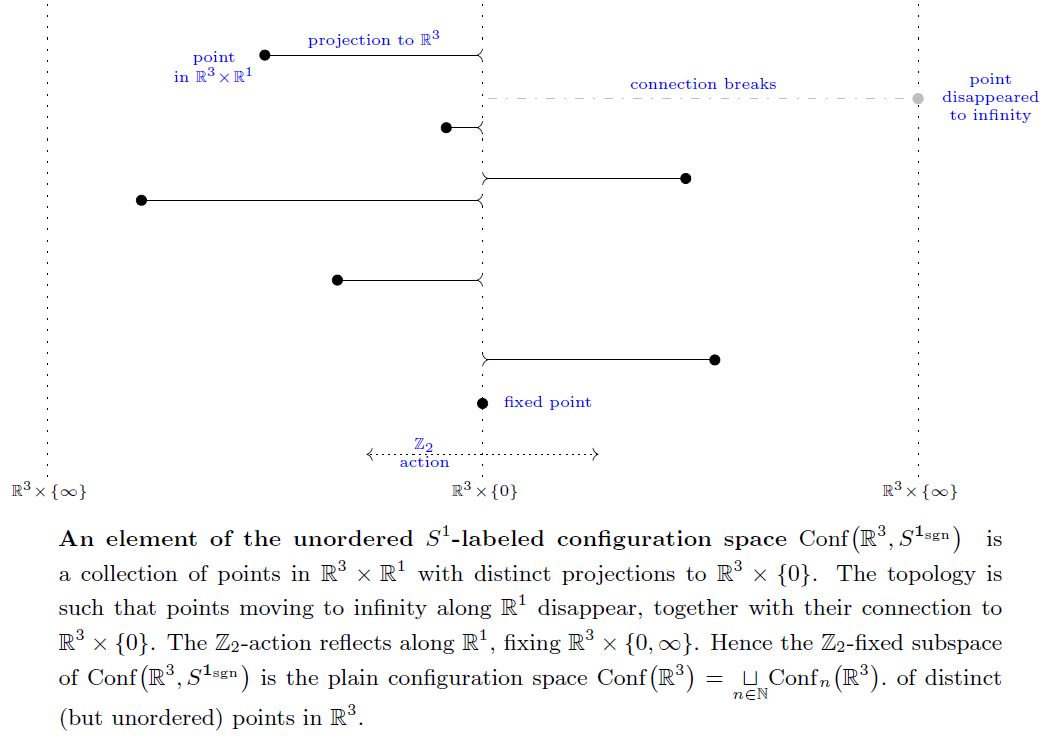
Definition
(unordered labeled configurations of a fixed number of points)
Let be a manifold, possibly with boundary. For , the configuration space of unordered points in disappearing at the boundary is the topological space
where is the fat diagonal in and where denotes the evident action of the symmetric group by permutation of factors of inside .
More generally, let be another manifold, possibly with boundary. For , the configuration space of points in vanishing at the boundary and distinct as points in is the topological space
where now denotes the evident action of the symmetric group by permutation of factors of inside .
This more general definition reduces to the previous case for being the point:
Finally the configuration space of an arbitrary number of points in vanishing at the boundary and distinct already as points of is the quotient topological space of the disjoint union space
by the equivalence relation given by
This is naturally a filtered topological space with filter stages
The corresponding quotient topological spaces of the filter stages reproduces the above configuration spaces of a fixed number of points:
Remark
(comparison to notation in the literature)
The above Def. is less general but possibly more suggestive than what is considered for instance in Bödigheimer 87. Concretely, we have the following translations of notation:
Notice here that when happens to have empty boundary, , then the pushout
is with a disjoint basepoint attached. Notably for the point space, we have that
is the 0-sphere.
A slight variation of the definition is sometimes useful:
Definition
(configuration space of -disks)
In the situation of Def. , with a manifold of dimension
be, on the left, the labeled configuration space of joint embeddings of tuples
of -dimensional disks/closed balls into , with identifications as in Def. (in particular the disks centered at the basepoint are quotiented out) and with the comparison map sending each disk to its center.
This map is evidently a deformation retraction hence in particular a homotopy equivalence.
Properties
Basic properties
Proposition
(forgetting points is a fibration)
Let be a topological manifold. For , the continuous map
which forgets the first points is a locally trivial fiber bundle with typical fiber . In particular it is a Hurewicz fibration.
Using this one may deduce that:
Proposition
(configuration space of points in plane is EM-space of braid group)
The homotopy type of a configuration space of points in the plane is that of an Eilenberg-MacLane space of the braid group in degree 1:
(Farber & Grant 08, Theorem 1)
Ordered unlabeled configurations from unordered labeled configurations
under construction
(…)
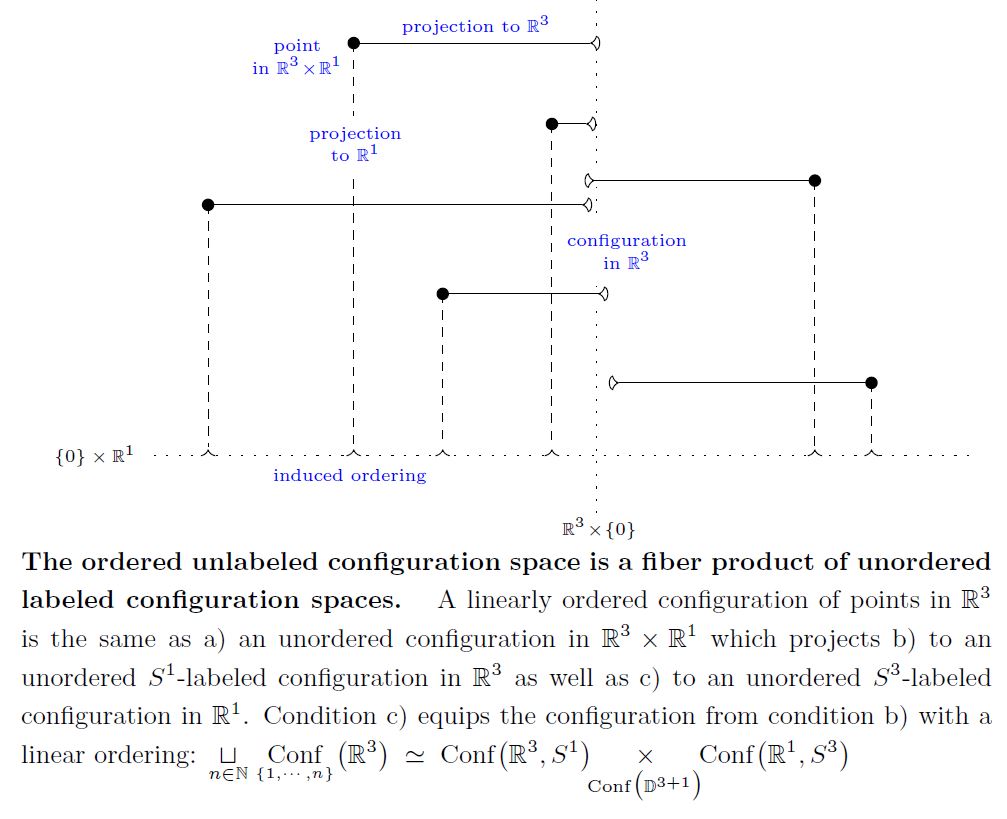
(…)
Cohomotopy charge map
The Cohomotopy charge map is the function that assigns to a configuration of points their total charge as measured in Cohomotopy-cohomology theory.
This is alternatively known as the “electric field map” (Salvatore 01 following Segal 73, Section 1, see also Knudsen 18, p. 49) or the “scanning map” (Kallel 98).
For the Cohomotopy charge map is the continuous function
from the configuration space of points in the Euclidean space to the -Cohomotopy cocycle space vanishing at infinity on the Euclidean space, which is equivalently the space of pointed maps from the one-point compactification to itself, and hence equivalently the -fold iterated based loop space of the D-sphere), which sends a configuration of points in , each regarded as carrying unit charge to their total charge as measured in Cohomotopy-cohomology theory (Segal 73, Section 3).
The construction has evident generalizations to other manifolds than just Euclidean spaces, to spaces of labeled configurations and to equivariant Cohomotopy. The following graphics illustrates the Cohomotopy charge map on G-space tori for with values in -equivariant Cohomotopy:
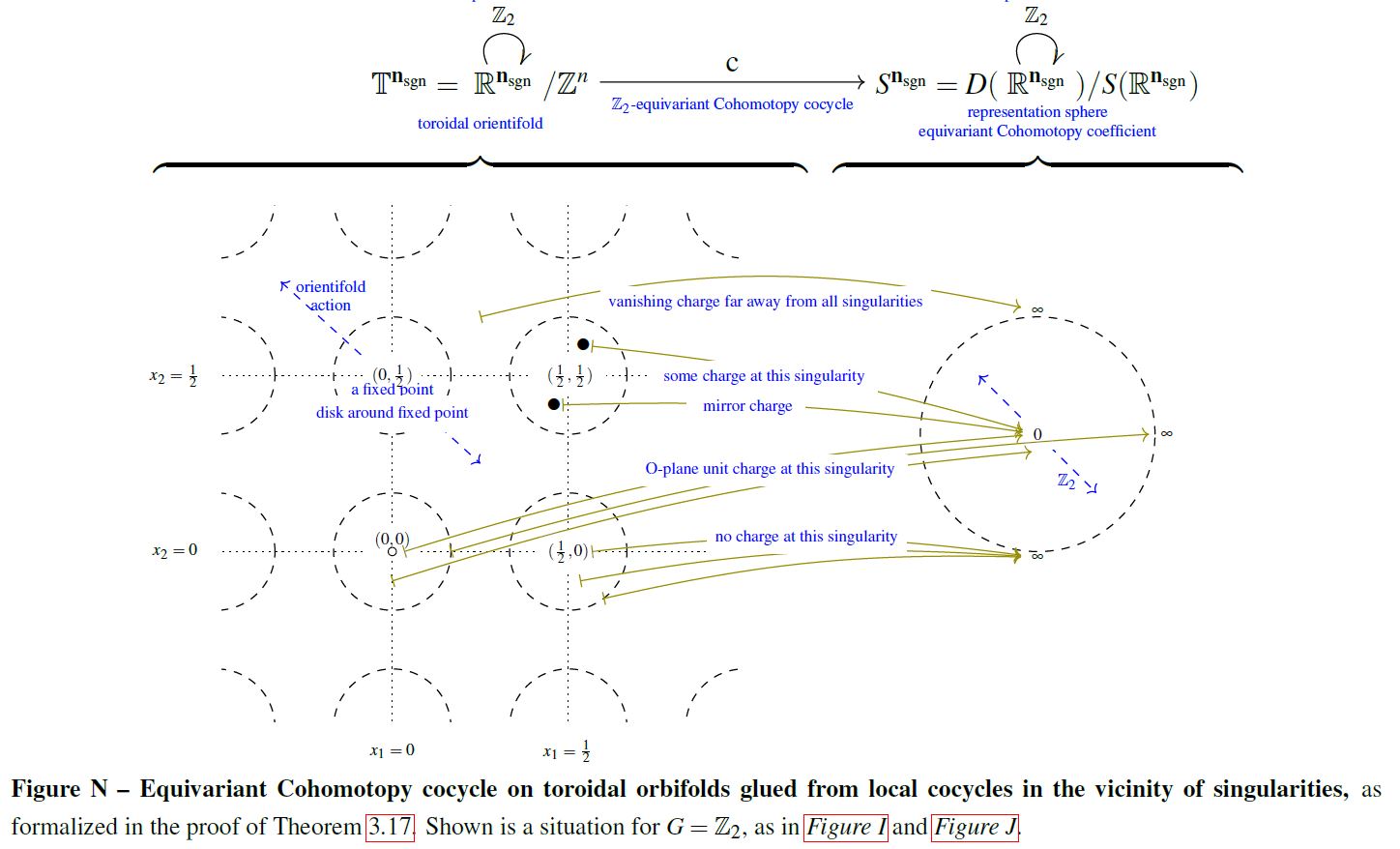
graphics grabbed from SS 19
Relation to iterated loop spaces of iterated suspensions
In some situations the Cohomotopy charge map is a weak homotopy equivalence and hence exhibits, for all purposes of homotopy theory, the Cohomotopy cocycle space of Cohomotopy charges as an equivalent reflection of the configuration space of points:
Proposition
(group completion on configuration space of points is iterated based loop space)
from the full unordered and unlabeled configuration space (2) of Euclidean space to the -fold iterated based loop space of the D-sphere, exhibits the group completion (3) of the configuration space monoid
Proposition
(Cohomotopy charge map is weak homotopy equivalence on sphere-labeled configuration space of points)
For with , the Cohomotopy charge map (9)
is a weak homotopy equivalence
-
from the configuration space (7) of unordered points with labels in and vanishing at the base point of the label space
-
to the -fold iterated loop space of the D+k-sphere
hence equivalently
- to the cocycle space of Cohomotopy cohomology theory in degree vanishing at infinity on Euclidean space of dimension .
This statement generalizes to equivariant homotopy theory, with equivariant configurations carrying charge in equivariant Cohomotopy:
Let be a finite group and an orthogonal -linear representation, with its induced pointed topological G-spaces:
-
the corresponding representation sphere ,
-
the corresponding Euclidean G-space .
For any pointed topological G-space, consider
-
the equivariant -suspension, given by the smash product with the -representation sphere:
-
the equivariant -iterated based loop space, given by the -fixed point subspace inside the space of maps out of the representation sphere:
.
Definition
(equivariant unordered labeled configurations vanishing with vanishing label)
Write
for the -fixed point subspace in the unordered -labelled configuration space of points (Def. ), with respect to the diagonal action on .
Proposition
(Cohomotopy charge map-equivalence for configurations on Euclidean G-spaces)
Let
If is -connected, in that for all subgroups the -fixed point subspace is a connected topological space, then the Cohomotopy charge map
from the equivariant un-ordered -labeled configuration space of points (Def. ) in the corresponding Euclidean G-space to the based -loop space of the -suspension of , is a weak homotopy equivalence.
If is not necessarily -connected, then this still holds for the group completion of the configuration space, under disjoint union of configurations
(Rourke & Sanderson 2000, Theorem 1, Theorem 2)
More generally:
Proposition
(iterated loop spaces equivalent to configuration spaces of points)
For
-
, a natural number with denoting the Cartesian space/Euclidean space of that dimension,
the Cohomotopy charge map constitutes a homotopy equivalence
between
-
the configuration space of arbitrary points in vanishing at the boundary (Def. )
-
the d-fold loop space of the -fold reduced suspension of the quotient space (regarded as a pointed topological space with basepoint ).
In particular when is the closed ball of dimension this gives a homotopy equivalence
with the d-fold loop space of the (d+k)-sphere.
(May 72, Theorem 2.7, Segal 73, Theorem 3, see Bödigheimer 87, Example 13)
Proposition
(stable splitting of mapping spaces out of Euclidean space/n-spheres)
For
-
, a natural number with denoting the Cartesian space/Euclidean space of that dimension,
there is a stable weak homotopy equivalence
between
-
the suspension spectrum of the configuration space of an arbitrary number of points in vanishing at the boundary and distinct already as points of (Def. )
-
the direct sum (hence: wedge sum) of suspension spectra of the configuration spaces of a fixed number of points in , vanishing at the boundary and distinct already as points in (also Def. ).
Combined with the stabilization of the Cohomotopy charge map homotopy equivalence from Prop. this yields a stable weak homotopy equivalence
between the latter direct sum and the suspension spectrum of the mapping space of pointed continuous functions from the d-sphere to the -fold reduced suspension of .
(Snaith 74, theorem 1.1, Bödigheimer 87, Example 2)
In fact by Bödigheimer 87, Example 5 this equivalence still holds with treated on the same footing as , hence with on the right replaced by in the well-adjusted notation of Def. :
Relation to classifying space of the symmetric group
Let . Then
-
the unordered configuration space of points in is a model for the classifying space of the symmetric group ;
(e.g. Bödigheimer 87, Example 10)
-
the ordered configuration space of points, equipped with the canonical -action, is a model for the -universal principal bundle.
Relation to James construction
The James construction of is homotopy equivalent to the configuration space of points of points in the real line with labels taking values in .
(e.g. Bödigheimer 87, Example 9)
In twisted Cohomotopy
The May-Segal theorem generalizes from Euclidean spaces to closed smooth manifolds if at the same time one passes from plain Cohomotopy to twisted Cohomotopy, namely twisted via the J-homomorphism, by the tangent bundle:
Proposition
Let
-
be a smooth closed manifold of dimension ;
Then the Cohomotopy charge map constitutes a weak homotopy equivalence
between
-
the tangentially-twisted (n+k)-Cohomotopy space of , hence the space of sections of the -spherical fibration over which is associated via the tangent bundle by the O(n)-action on
-
the configuration space of points on with labels in .
(Bödigheimer 87, Prop. 2, following McDuff 75, reviewed in Kallel 2024, Thm. 4.2)
Remark
In the special case that the closed manifold in Prop. is parallelizable, hence that its tangent bundle is trivializable, the statement of Prop. reduces to this:
Let
-
be a parallelizable closed manifold of dimension ;
Then the Cohomotopy charge map constitutes a weak homotopy equivalence
between
-
-Cohomotopy space of , hence the space of maps from to the (n+k)-sphere
-
the configuration space of points on with labels in .
Rational maps to complex projective space
A similar relation holds for mapping spaces not to spheres, but to complex projective spaces:
Proposition
The homotopy type of the space of rational maps from the Riemann sphere to complex projective -space of algebraic degree is that of the configuration space of at most points in with labels in :
(Cohen & Shimamoto 91, Theorem 1)
Knizhnik-Zamolodchicov connection
For the Definition of the Knizhnik-Zamolodchikov connection we need the following notation:
-
configuration spaces of points
For write
(11)for the ordered configuration space of n points in the plane, regarded as a smooth manifold.
Identifying the plane with the complex plane , we have canonical holomorphic coordinate functions
(12) -
(13)
for the quotient vector space of the linear span of horizontal chord diagrams on strands by the 4T relations (infinitesimal braid relations), regarded as an associative algebra under concatenation of strands (here).
Definition
The universal Knizhnik-Zamolodchikov form is the horizontal chord diagram-algebra valued differential form (13) on the configuration space of points (11)
given in the canonical coordinates (12) by:
where

is the horizontal chord diagram with exactly one chord, which stretches between the th and the th strand.
Regarded as a connection form for a connection on a vector bundle, this defines the universal Knizhnik-Zamolodchikov connection , with covariant derivative
for any smooth function
with values in modules over the algebra of horizontal chord diagrams modulo 4T relations.
The condition of covariant constancy
is called the Knizhnik-Zamolodchikov equation.
Finally, given a metric Lie algebra and a tuple of Lie algebra representations
the corresponding endomorphism-valued Lie algebra weight system
turns the universal Knizhnik-Zamolodchikov form (14) into a endomorphism ring-valued differential form
The universal formulation (14) is highlighted for instance in Bat-Natan 95, Section 4.2, Lescop 00, p. 7. Most authors state the version after evaluation in a Lie algebra weight system, e.g. Kohno 14, Section 5.
Proposition
(Knizhnik-Zamolodchikov connection is flat)
The Knizhnik-Zamolodchikov connection (Def. ) is flat:
Proposition
(Kontsevich integral for braids)
The Dyson formula for the holonomy of the Knizhnik-Zamolodchikov connection (Def. ) is called the Kontsevich integral on braids.
(e.g. Lescop 00, side-remark 1.14)
Action by little -disk operad and by Goodwillie derivatives
Under some conditions and with suitable degrees/shifts, configuration spaces of points canonically have the structure of algebras over an operad over the little n-disk operad and the Goodwillie derivatives of the identitity functor?.
For more see there
Homology and stabilization in homology
Let be a topological space which is the interior of a compact manifold with boundary . We may think of the boundary as consisting of the “points at infinity” in .
In particular, there are then inclusion maps
of the unordered configuration space of points in (Def. ) into that of points, formalizing the idea of “adding a point at infinity” to a configuration. More formally, these maps are given by pushing configuration points away from the boundary a little and then adding a new point near to a point on the boundary of .
(Randal-Williams 13, Section 4)
The homotopy class of these maps depends (just) on the connected component of the boundary at which one chooses to bring in the new point. But for any choice, they have the following effect on cycles in ordinary homology:
Proposition
(homological stabilization for unordered configuration spaces)
Let be
-
which is the interior of a compact manifold with boundary
-
of dimension .
Then for all the inclusion maps (17) are such that on ordinary homology with integer coefficients these maps induce split monomorphisms in all degrees,
and in degrees these are even isomorphisms
Finally, for ordinary homology with rational coefficients, these maps induce isomorphisms all the way up to degree :
(Randal-Williams 13, Theorem A and Threorem B)
Gauss-Manin connections
On Gauss-Manin connections over configuration spaces of points:
-
Daniel C. Cohen, Peter Orlik, Gauss-Manin Connections for Arrangements, I Eigenvalues, Compositio Math. 136 (2003) 299-316 arXiiv:math/0105063, doi:10.1023/A:1023262022279
-
Daniel C. Cohen, Peter Orlik, Gauss-Manin connections for arrangements, II Nonresonant weights, Amer. J. Math. 127 (2005) 569-594 arXiv:math/0207114, jstor:40067930
-
Daniel C. Cohen, Peter Orlik, Gauss-Manin connections for arrangements, III Formal connections, Trans. Amer. Math. Soc. 357 (2005) 3031-3050 arXiv:math/0307210, doi:10.1090/S0002-9947-04-03621-9
and review in the context of hypergeometric solutions to the Knizhnik-Zamolodchikov equation:
- Pavel Etingof, Igor Frenkel, Alexander Kirillov, Section 7.5 in: Lectures on Representation Theory and Knizhnik-Zamolodchikov Equations, Mathematical surveys and monographs 58, American Mathematical Society (1998) ISBN:978-1-4704-1285-2, review pdf
Rational homotopy type
We discuss aspects of the rational homotopy type of configuration spaces of points. See also at graph complex.
Rational cohomology
Proposition
(real cohomology of configuration spaces of ordered points in Euclidean space)
The real cohomology ring of the configuration spaces (Def. ) of ordered unlabeled points in Euclidean space
is generated by elements in degree
for
subject to these three relations:
-
(anti-)symmetry)
-
nilpotency
-
3-term relation
Hence:
This is due to Cohen 1976, following Arnold 1969 and Cohen 1073. See also Félix & Tanré 2003, Section 2; Lambrechts & Tourtchine 2009, Section 3.
See also at Fulton-MacPherson compactification the section de Rham cohomology.
Remark
(real cohomology of the configuration space in terms of graph cohomology)
In the graph complex-model for the rational homotopy type of the ordered unlabeled configuration space of points the three relations in Prop. are incarnated as follows:
-
a graph changes sign when one of its edges is reversed (this Def.)
-
a graph with parallel edges is a vanishing graph (this Def.)
-
the graph coboundary of a single trivalent internal vertex (this Example).
Rational homotopy and Whitehead products
Write again
for the configuration space of ordered points in Euclidean space.
Proposition
The Whitehead product super Lie algebra of rationalized homotopy groups
is generated from elements
subject to the following relations:
-
if are pairwise distinct;
-
.
This is due to Kohno 02. See also Lambrechts-Tourtchine 09, Section 3.
Relation to weight systems, chord diagrams and Vassiliev invariants
weight systems are cohomology of loop space of configuration space:
Proposition
(integral horizontal weight systems are integral cohomology of based loop space of ordered configuration space of points in Euclidean space)
For ground ring the integers, there is, for each natural number , a canonical isomorphism of graded abelian groups between
-
the integral weight systems
on horizontal chord diagrams of strands (elements of the set )
-
the integral cohomology of the based loop space of the ordered configuration space of n points in 3d Euclidean space:
(the second equivalence on the right is the fact that weight systems are associated graded of Vassiliev invariants).
This is stated as Kohno 02, Theorem 4.1
Proposition
(weight systems are inside real cohomology of based loop space of ordered configuration space of points in Euclidean space)
For ground field the real numbers, there is a canonical injection of the real vector space of framed weight systems (here) into the real cohomology of the based loop spaces of the ordered configuration spaces of points in 3-dimensional Euclidean space:
This is stated as Kohno 02, Theorem 4.2
| chord diagrams | weight systems |
|---|---|
| linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams | Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems |
Berry-Robbins and Atiyah-Sutcliffe construction
In the course of providing a geometric-proof of the spin-statistics theorem, Berry & Robbins 1997 asked, at each natural number , for a continuous and -equivariant function
-
from the configuration space of points (ordered and unlabeled) in Euclidean space
-
to the coset space of the unitary group by its maximal torus, hence the complete flag manifold of flags in ,
both equipped with the evident group action by the symmetric group .
For the first non-empty case this readily reduces to asking for a continuous map of the form which is equivariant with respect to passage to antipodal points. This is immediately seen to be given by the radial projection. But this special case turns out not to be representative of the general case, as this simple construction idea does not generalize to .
That a continuous and -equivariant Berry-Robbins map (19) indeed exists for all was proven in Atiyah 2000.
In this article, Atiyah turned attention to the stronger question asking for a smooth and -equivariant function (19) and provided an elegant proof strategy for this stronger statement, which however hinges on some conjectural positivity properties of a certain determinant (discussed in more detail and with first numerical evidence in Atiyah 2001), interpreted as the electrostatic energy of -particles in .
Extensive numerical checks of this stronger but conjectural construction was recorded, up to , in Atiyah & Sutcliffe 2002, together with a refined formulation of the conjecture, whence it came to be known as the Atiyah-Sutcliffe conjecture.
The Atiyah-Sutcliffe conjecture has been proven for in Atiyah 2000/01 and for by Eastwood & Norbury 01. A general proof is claimed in Atiyah & Malkoun 18.
Occurrences and Applications
Compactification
The Fulton-MacPherson compactification of configuration spaces of points in serves to exhibit them as models for the little n-disk operad.
Stable splitting of mapping spaces
The stable splitting of mapping spaces says that suspension spectra of suitable mapping spaces are equivalently wedge sums of suspension spectra of configuration spaces of points.
Correlators as differential forms on configuration spaces
In Euclidean field theory the correlators are often regarded as distributions of several variables with singularities on the fat diagonal. Hence they become non-singular distributions after restriction of distributions to the corresponding configuration space of points.
For more on this see at correlators as differential forms on configuration spaces of points.
Related concepts
References
General
The braid group regarded as the fundamental group of a configuration space of points is considered (neither of them under these names, though) already in:
- Adolf Hurwitz, §II of: Über Riemann’sche Flächen mit gegebenen Verzweigungspunkten, Mathematische Annalen 39 (1891) 1–60 [doi:10.1007/BF01199469]
there regarded as acting on Riemann surfaces forming branched covers, by movement of the branch points.
The concept of configuration spaces is then re-discovered/re-vived by:
-
Edward Fadell, Lee Neuwirth, Configuration spaces, Math. Scand. 10 (1962) 111-118 [doi:10.7146/math.scand.a-10517, pdf, MR141126]
-
Ralph H. Fox, Lee Neuwirth, The braid groups, Math. Scand. 10 (1962) 119-126
[doi:10.7146/math.scand.a-10518, pdf, pdf, MR150755]
(focus on the resulting braid groups)
See also early occurences in physics, listed below.
General accounts:
-
Edward Fadell, Sufian Husseini, Geometry and topology of configuration spaces, Springer Monographs in Mathematics (2001) [doi:10.1007/978-3-642-56446-8, MR2002k:55038]
-
Frederick R. Cohen: Introduction to configuration spaces and their applications, in: Braids, Lecture Notes Series 19, Institute for Mathematical Sciences, National University of Singapore (2009) 183-261 [doi:10.1142/9789814291415_0003, doi:10.1142/7550, pdf, pdf]
-
Neil Strickland, section 3 of: A Bestiary of Topological Objects [pdf, pdf]
-
Craig Westerland, Configuration spaces in geometry and topology (2011) [pdf]
-
Ben Knudsen, Configuration spaces in algebraic topology [arXiv:1803.11165]
(in algebraic topology)
-
Lucas Williams: Configuration Spaces for the Working Undergraduate, Rose-Hulman Undergraduate Mathematics Journal 21 1 (2020) Article 8 [arXiv:1911.11186, rhumj:vol21/iss1/8]
-
Sadok Kallel, Configuration spaces of points: A user’s guide, Encyclopedia of Mathematical Physics 2nd ed 4 (2025) 98-135 [arXiv:2407.11092, doi:10.1016/B978-0-323-95703-8.00211-1]
In relation to braid groups:
- Joan S. Birman: Braids, links, and mapping class groups, Princeton Univ Press (1975) [ISBN:9780691081496, preview pdf]
In relation to the space of finite subsets:
-
David Handel, Some Homotopy Properties of Spaces of Finite Subsets of Topological Spaces, Houston Journal of Mathematics, Electronic Edition Vol. 26, No. 4, 2000 (pdfhjm:Vol26-4)
-
Yves Félix, Daniel Tanré Rational homotopy of symmetric products and Spaces of finite subsets, Contemp. Math 519 (2010): 77-92 (pdf)
In relation to graph complexes:
- Ricardo Campos: Configuration Spaces of Points, CIM Bulletin 41 (2020) 41-47 [pdf, hal:03754254]
The algebra-structure of configuration spaces over little n-disk operads/Fulton-MacPherson operads:
- Martin Markl, A compactification of the real configuration space as an operadic completion, J. Algebra 215 1 (1999) 185–204 [arXiv:hep-th/9608067, doi:10.1006/jabr.1998.7709]
On topological complexity of configuration space:
- Michael Farber, Mark Grant, Topological Complexity of the Klein bottle (2008), arXiv:0806.4111
Cohomotopy charge map
The Cohomotopy charge map (“electric field map”, “scanning map”) and hence the relation of configuration spaces to Cohomotopy goes back to
-
Peter May, The geometry of iterated loop spaces, Springer (1972) [doi:10.1007/BFb0067491, pdf]
-
Graeme Segal, Configuration-spaces and iterated loop-spaces, Invent. Math. 21 (1973) 213-221 [doi:10.1007/BF01390197, pdf, MR 0331377]
Generalization of these constructions and results is due to
-
Dusa McDuff, Configuration spaces of positive and negative particles, Topology 14 1 (1975) 91-107 [doi:10.1016/0040-9383(75)90038-5, pdf]
-
Dusa McDuff: Configuration Spaces, in: K-Theory and Operator Algebras, Lecture Notes in Mathematics 575 Springer (1977) 88-95 [doi:10.1007/BFb0095704, pdf]
-
Carl-Friedrich Bödigheimer, Stable splittings of mapping spaces, in: Algebraic topology, Lecture Notes in Mathematics 1286, Springer (1987) 174-187 [pdf, pdf, doi:10.1007/BFb0078741]
-
Richard Manthorpe, Ulrike Tillmann, Tubular configurations: equivariant scanning and splitting, Journal of the London Mathematical Society, Volume 90, Issue 3 (arxiv:1307.5669, doi:10.1112/jlms/jdu050)
-
J. Caruso, Stefan Waner: An Approximation to , Transactions of the American Mathematical Society 265 1 (1981) 147-162 [doi:10.2307/1998487, jstor:1998487, pdf]
-
J. Caruso, Stefan Waner: An approximation theorem for equivariant loop spaces in the compact Lie case, Pacific J. Math. 117 1 (1985) 27-49 [euclid:pjm/1102706926]
-
Shingo Okuyama: A simple solution for a group completion problem, Trends in Mathematics 7 1 (2004) 69-74 [pdf, pdf]
-
Shingo Okuyama: The space of intervals in a Euclidean space, Algebr. Geom. Topol. 5 (2005) 1555-1572 [arXiv:math/0511645, doi:10.2140/agt.2005.5.1555]
-
Kazuhisa Shimakawa: Labeled configuration spaces and group completions, Forum Mathematicum (2007) 353-364 [doi:10.1515/FORUM.2007.014, pdf]
-
Shingo Okuyama, Kazuhisa Shimakawa, Interactions of strings and equivariant homology theories, Geom. Topol. Monogr. 10 (2007) 333-346 [arXiv:0903.4667, doi:10.2140/gtm.2007.10.333]
Generalization to equivariant homotopy theory:
- Colin Rourke, Brian Sanderson, Equivariant Configuration Spaces, J. London Math. Soc. 62 (2000) 544-552 [arXiv:math/9712216, doi:10.1112/S0024610700001241]
and strengthening in the special case :
- Miguel A. Xicoténcatl, On -equivariant loop spaces, in: Recent developments in algebraic topology, Contemp. Math. 407, AMS (2006) 183—191 [ams:CONM/407, pdf]
partly based on
-
Henning Hauschild: Zerspaltung äquivarianter Homotopiemengen, Math. Ann. 230 (1977) 279-292 [pdf]
-
Graeme Segal, Some results in equivariant homotopy theory (1978) [scan: web, pdf]
and generalization to compact Lie groups:
The relevant construction for the group completion of the configuration space
-
Paolo Salvatore, Configuration spaces with summable labels, In: Aguadé J., Broto C., Carles Casacuberta (eds.) Cohomological Methods in Homotopy Theory. Progress in Mathematics 196 Birkhäuser (2001) [arXiv:math/9907073]
and from the point of view of cobordism categories:
- Oscar Randal-Williams, section 10 of: Embedded Cobordism Categories and Spaces of Manifolds, Int. Math. Res. Not. IMRN 2011, no. 3, 572-608 (arXiv:0912.2505)
On the homotopy type of the space of rational functions from the Riemann sphere to itself (related to the moduli space of monopoles in and to the configuration space of points in ):
- Graeme Segal, The topology of spaces of rational functions, Acta Math. Volume 143 (1979), 39-72 (euclid:1485890033)
See also
-
Sadok Kallel, Spaces of particles on manifolds and Generalized Poincaré Dualities, The Quarterly Journal of Mathematics, Volume 52, Issue 1, 1 March 2001 (doi:10.1093/qjmath/52.1.45)
-
Shingo Okuyama, Kazuhisa Shimakawa, Interactions of strings and equivariant homology theories, Geom. Topol. Monogr. 10 (2007) 333-346 [arXiv:0903.4667, doi:10.2140/gtm.2007.10.333]
For relation to instantons via topological Yang-Mills theory:
- Michael Atiyah, John David Stuart Jones, Topological aspects of Yang-Mills theory, Comm. Math. Phys. Volume 61, Number 2 (1978), 97-118 (arXiv:1103904210)
An analogous statement for homotopy of rational maps related to Yang-Mills monopoles:
- Ralph L. Cohen, Don H. Shimamoto, Rational Functions, Labelled Configurations, and Hilbert Schemes, Journal of the London Mathematical Socienty 43 2 (1991) 509-528 (doi:10.1112/jlms/s2-43.3.509)
In the context of speculations regarding Galois theory over the sphere spectrum:
- Jack Morava, Jonathan Beardsley, Toward a Galois theory of the integers over the sphere spectrum, Journal of Geometry and Physics Volume 131, September 2018, Pages 41-51 (arXiv:1710.05992)
Stable splitting of mapping spaces
The appearance of configuration spaces as summands in stable splittings of mapping spaces is originally due to
- Victor Snaith, A stable decomposition of , Journal of the London Mathematical Society 7 (1974), 577 - 583 (pdf)
An alternative proof is due to
- Ralph Cohen, Stable proof of stable splittings, Math. Proc. Camb. Phil. Soc., 1980, 88, 149 (doi:10.1017/S030500410005742X, pdf)
Review and generalization is in
and the relation to the Goodwillie-Taylor tower of mapping spaces is pointed out in
In Goodwillie-calculus
The configuration spaces of a space appear as the Goodwillie derivatives of its mapping space/nonabelian cohomology-functor :
-
Greg Arone, A generalization of Snaith-type filtration, Transactions of the American Mathematical Society 351.3 (1999): 1123-1150. (pdf)
-
Michael Ching, Calculus of Functors and Configuration Spaces, Conference on Pure and Applied Topology Isle of Skye, Scotland, 21-25 June, 2005 (pdf)
Compactification
A compactification of configuration spaces of points was introduced in
- William Fulton, Robert MacPherson, A compactification of configuration spaces, Ann. of Math. (2), 139(1):183–225, 1994.
and an operad-structure defined on it (Fulton-MacPherson operad) in
- Ezra Getzler, John Jones, Operads, homotopy algebra and iterated integrals for double loop spaces (arXiv:hep-th/9403055)
Review includes
- Pascal Lambrechts, Ismar Volić, section 5 of Formality of the little -disks operad, Memoirs of the American Mathematical Society ; no. 1079, 2014 (arXiv“0808.0457, doi:10.1090/memo/1079)
This underlies the models of configuration spaces by graph complexes, see there for more.
Homology and cohomology
General discussion of ordinary homology/ordinary cohomology of configuration spaces of points:
-
Vladimir Arnold, The cohomology ring of the colored braid group, Mat. Zametki, 1969, Volume 5, Issue 2, Pages 227–231 (mathnet:mz6827)
-
Fred Cohen, Cohomology of braid spaces, Bull. Amer. Math. Soc. Volume 79, Number 4 (1973), 763-766 (euclid:1183534761)
-
Fred Cohen, The homology of -Spaces, , In: The Homology of Iterated Loop Spaces, Lecture Notes in Mathematics, vol 533. Springer 1976 (doi:10.1007/BFb0080467)
-
Carl-Friedrich Bödigheimer, Fred Cohen, L. Taylor, On the homology of configuration spaces, Topology Vol. 28 No. 1, p. 111-123 1989 (pdf)
-
E. Ossa, On the cohomology of configuration spaces, In: Broto C., Carles Casacuberta, Mislin G. (eds.), Algebraic Topology: New Trends in Localization and Periodicity, Progress in Mathematics, vol 136. Birkhäuser Basel (1996) (doi:10.1007/978-3-0348-9018-2_26)
-
Yves Félix, Jean-Claude Thomas, Rational Betti numbers of configuration spaces, Topology and its Applications, Volume 102, Issue 2, 8 April 2000, Pages 139-149 (doi:10.1016/S0166-8641(98)00148-5)
-
Oscar Randal-Williams, Homological stability for unordered configuration spaces, The Quarterly Journal of Mathematics, Volume 64, Issue 1, March 2013, Pages 303–326 (arXiv:1105.5257)
-
Yves Félix, Daniel Tanré, The cohomology algebra of unordered configuration spaces, Journal of the LMS, Vol 72, Issue 2 (arxiv:math/0311323, doi:10.1112/S0024610705006794)
-
Martin Palmer, Configuration spaces and homological stability, Oxford University Research Archive (2012) [pdf, web, pdf]
-
Ben Knudsen, Betti numbers and stability for configuration spaces via factorization homology, Algebr. Geom. Topol. 17 (2017) 3137-3187 (arXiv:1405.6696)
-
Thomas Church, Homological stability for configuration spaces of manifolds (arxiv:1602.04748)
-
Christoph Schiessl, Betti numbers of unordered configuration spaces of the torus (arxiv:1602.04748)
-
Christoph Schiessl, Integral cohomology of configuration spaces of the sphere (arxiv:1801.04273)
-
Weiyan Chen, Twisted cohomology of configuration spaces and spaces of maximal tori via point-counting (arXiv:1603.03931)
-
Dan Petersen, Cohomology of generalized configuration spaces (arXiv:1807.07293)
-
Victor Vassiliev, Twisted homology of configuration spaces, homology of spaces of equivariant maps, and stable homology of spaces of non-resultant systems of real homogeneous polynomials (arXiv:1809.05632)
-
Victor Vassiliev, Cohomology of spaces of Hopf equivariant maps of spheres (arXiv:2102.07157)
-
Roberto Pagaria, The cohomology rings of the unordered configuration spaces of the torus, Algebr. Geom. Topol. 20 (2020) 2995–3012 (doi:10.2140/agt.2020.20.2995)
-
Christian Blanchet, Martin Palmer, Awais Shaukat, Heisenberg homology on surface configurations [arXiv:2109.00515]
-
Awais Shaukat, Christian Blanchet, Weakly framed surface configurations, Heisenberg homology and Mapping Class Group action, Archiv der Mathematik 120 (2023) 99–109 [arXiv:2206.11475, doi:10.1007/s00013-022-01793-3]
-
Christian Blanchet, Heisenberg homologies of surface configurations, talk at QFT and Cobordism, CQTS (Mar 2023) [web]
On the Hopf algebra structure of configuration spaces of disks:
- Stephen Bigelow, Jules Martel, Quantum groups from homologies of configuration spaces [arXiv:2405.06982]
For more references on the twisted cohomology of configuration spaces of points see at
Review with focus on the phenomenon of representation stability:
- Rita Jimenez Rolland, Jennifer C. H. Wilson, Stability properties of moduli spaces, Notices of the AMS 69 4 (April 2022) [arXiv:2201.04096, pdf, web]
Expressing the rational cohomology of ordered configuration spaces of points via factorization homology and Ran spaces:
- Quoc P. Ho, Higher representation stability for ordered configuration spaces and twisted commutative factorization algebras (arXiv:2004.00252)
Discussion of the Morava E-theory of configuration spaces of points:
- Lukas Brantner, Jeremy Hahn, Ben Knudsen, The Lubin-Tate Theory of Configuration Spaces: I (arXiv:1908.11321)
Homotopy
Discussion of homotopy groups of configuration spaces:
-
Pascal Lambrechts, Victor Tourtchine, Homotopy graph-complex for configuration and knot spaces, Transactions of the AMS, Volume 361, Number 1, January 2009, Pages 207–222 (arxiv:math/0611766)
-
Sadok Kallel, Ines Saihi, Homotopy Groups of Diagonal Complements, Algebr. Geom. Topol. 16 (2016) 2949-2980 (arXiv:1306.6272)
Rational homotopy type
Discussion of the rational homotopy type of configuration spaces of points:
-
Igor Kriz, On the Rational Homotopy Type of Configuration Spaces, Annals of Mathematics
Second Series 139 2 (1994) 227-237 [jstor:2946581]
-
Najib Idrissi, Real homotopy of configuration spaces, Peccot Lecture, Collège de France, March & May 2020, Spinger (2022) [doi:10.1007/978-3-031-04428-1, webpage, hal:03821309]
Cohomology modeled by graph complexes
That the de Rham cohomology of (the Fulton-MacPherson compactification of) configuration spaces of points may be modeled by graph complexes (exhibiting formality of the little n-disk operad) is due to
- Maxim Kontsevich, around Def. 15 and Lemma 3 in Operads and Motives in Deformation Quantization, Lett.Math.Phys.48:35-72,1999 (arXiv:math/9904055)
nicely reviewed in Lambrechts-Volic 14
Further discussion of graph complexes as models for the de Rham cohomology of configuration spaces of points:
-
Najib Idrissi, The Lambrechts-Stanley Model of Configuration Spaces, Invent. Math (2018) [arXiv:1608.08054, doi:10.1007/s00222-018-0842-9]
-
Ricardo Campos, Thomas Willwacher, A model for configuration spaces of points (arXiv:1604.02043)
-
Ricardo Campos, Najib Idrissi, Pascal Lambrechts, Thomas Willwacher, Configuration Spaces of Manifolds with Boundary [arXiv:1802.00716]
-
Ricardo Campos, Julien Ducoulombier, Najib Idrissi, Thomas Willwacher, A model for framed configuration spaces of points [arXiv:1807.08319]
Loop spaces of configuration spaces of points
On loop spaces of configuration spaces of points:
- Edward Fadell, Sufian Husseini, The space of loops on configuration spaces and the Majer-Terracini index, Topol. Methods Nonlinear Anal. Volume 11, Number 2 (1998), 249-271 (euclid:tmna/1476842829)
Specifically on ordinary homology/ordinary cohomology of based loop spaces of configuration spaces of points and the relation to weight systems/Vassiliev invariants:
-
Toshitake Kohno, Vassiliev invariants and de Rham complex on the space of knots,
In: Yoshiaki Maeda, Hideki Omori, Alan Weinstein (eds.), Symplectic Geometry and Quantization, Contemporary Mathematics 179 (1994): 123-123 (doi:10.1090/conm/179)
-
Fred Cohen, Samuel Gitler, Loop spaces of configuration spaces, braid-like groups, and knots, In: Jaume Aguadé, Carles Broto, Carles Casacuberta (eds.) Cohomological Methods in Homotopy Theory. Progress in Mathematics, vol 196. Birkhäuser, Basel 2001 (doi:10.1007/978-3-0348-8312-2_7)
-
Toshitake Kohno, Loop spaces of configuration spaces and finite type invariants, Geom. Topol. Monogr. 4 (2002) 143-160 (arXiv:math/0211056)
-
Fred Cohen, Samuel Gitler, On loop spaces of configuration spaces, Trans. Amer. Math. Soc. 354 (2002), no. 5, 1705–1748, (jstor:2693715, MR2002m:55020)
For more see also at weight systems are cohomology of loop space of configuration space.
Graph configuration spaces
On configuration spaces of points any two of which are required to be non-coincident only if connected by an edge in a labelin graph:
- Sadok Kallel, The Homotopy Type of Graph Configuration Spaces, talk at CQTS (Oct 2023) [slides:pdf, video:YT]
Configurations in general position
Discussion of spaces of configurations of points “in general position”, where not only any pair of points is required to be non-coincident, but any -tuple is required to span an -dimensional subspace, typically considered after projective quotienting:
-
Mikhail Kapranov, §2.1 in: Chow quotients of Grassmannian I, Advances in Soviet Mathematics 16 (1993) 29–110 [arXiv:alg-geom/9210002]
-
Nima Arkani-Hamed, Thomas Lam, Marcus Spradlin, Positive configuration space, Commun. Math. Phys. 384 (2021) 909–954 [arXiv:2003.03904, doi:10.1007/s00220-021-04041-x]
In quantum (field) theory
Discussion/proof of the spin-statistics theorem for non-relativistic particles via the topology/homotopy theory of their configuration spaces of points (cf. also braid group statistics):
-
Michael G. G. Laidlaw, Cécile Morette DeWitt, Feynman Functional Integrals for Systems of Indistinguishable Particles, Phys. Rev. D 3 6 (1971) 1375-1378 [doi:10.1103/PhysRevD.3.1375]
-
A. P. Balachandran, A. Daughton, Z. C. Gu, Giuseppe Marmo, Rafael D. Sorkin Spin statistics theorems without relativity or field theory, Int. J. Mod. Phys. A 8 (1993) 2993-3044 [doi:10.1142/S0217751X93001223]
-
Michael V. Berry, Jonathan M. Robbins, Indistinguishability for quantum particles: spin, statistics and the geometric phase, Proceedings of the Royal Society A 453 1963 (1997) 1771-1790 [doi:10.1098/rspa.1997.0096]
(cf. also the Atiyah-Sutcliffe conjecture)
-
Michael V. Berry, Jonathan M. Robbins: Quantum indistinguishability: alternative constructions of the transported basis, J. Phys. A: Math. Gen. 33 (2000) L207 [doi:10.1088/0305-4470/33/24/101, pdf]
-
Murray Peshkin: Spin and Statistics in Nonrelativistic Quantum Mechanics: The Zero Spin Case, Phys. Rev.A 67 (2003) 042102 [doi:10.1103/PhysRevA.67.042102, arXiv:quant-ph/0207017]
-
Charis Anastopoulos, International Journal of Modern Physics A 19 05 (2004) 655-676 [doi:10.1142/S0217751X04017860, arXiv:quant-ph/0110169]
(via geometric quantization)
-
Nikolaos A. Papadopoulos, Mario Paschke, Andrés F. Reyes-Lega, F. Florian Scheck, The spin-statistics relation in nonrelativistic quantum mechanics and projective modules, Annales Mathematiques Blaise Pascal 11 (2004) 205-220 [doi:10.5802/ambp.193, arXiv:quant-ph/0608125, numdam:AMBP_2004__11_2_205_0/]
-
J. M. Harrison, Jonathan M. Robbins, Quantum indistinguishability from general representations of , J. Math. Phys. 45 (2004) 1332–1358 [doi:10.1063/1.1666979, arXiv:math-ph/0302037]
-
Bernd Kuckert, Spin and statistics in nonrelativistic quantum mechanics, I, Physics Letters A 322 1–2 (2004) 1–2 47-53 [doi:10.1016/j.physleta.2003.12.051, arXiv:quant-ph/0208151]
-
Bernd Kuckert, Jens Mund, Spin & Statistics in Nonrelativistic Quantum Mechanics, II, Ann. Phys. 517 5 (2005) 309-311 [doi:10.1002/andp.200410129, arXiv:quant-ph/0411197]
-
Murray Peshkin: Spin-Zero Particles must be Bosons: A New Proof within Nonrelativistic Quantum Mechanics, Found Phys 36 (2006) 19–29 [doi:10.1007/s10701-005-9011-2]
-
Nikolaos A. Papadopoulos Andrés F. Reyes-Lega: On the Geometry of the Berry-Robbins Approach to Spin-Statistics, Found Phys 40 (2010) 829-851 [doi:10.1007/s10701-009-9365-y, arXiv:0910.1659]
-
Andrés F. Reyes-Lega, Carlos Benavides, Remarks on the Configuration Space Approach to Spin-Statistics, Found Phys 40 (2010) 1004-1029 [doi:10.1007/s10701-009-9397-3, arXiv:0911.0579]
-
Andrés F. Reyes-Lega: On the geometry of quantum indistinguishability, J. Phys. A: Math. Theor. 44 33 (2011) 325308 [doi:10.1088/1751-8113/44/32/325308, arXiv:1112.6300]
-
Jonathan Bain: Non-RQFT Derivations of CPT Invariance and the Spin–Statistics Connection, Chapter 4 in: CPT Invariance and the Spin-Statistics Connection, Oxford University Press (2016) [doi:10.1093/acprof:oso/9780198728801.003.0005, ISBN:9780198728801]
-
Michael Berry, Jonathan Robbins: Quantum Indistinguishability: Spin-statistics without Relativity or Field Theory?, in: A Half-Century of Physical Asymptotics and Other Diversions – Selected Works by Michael Berry, World Scientific (2017) 108-120 [doi:10.1142/9789813221215_0009, pdf]
In solid state physics/particle physics the configuration space of points appears early on in the discussion of anyon statistics, originally in:
-
Michael G. G. Laidlaw, Cécile Morette DeWitt, Feynman Functional Integrals for Systems of Indistinguishable Particles, Phys. Rev. D 3 (1971) 1375 doi:10.1103/PhysRevD.3.1375
-
Jon Magne Leinaas, Jan Myrheim, pp. 22 of: On the theory of identical particles, К теории тождествениых частиц, Nuovo Cim B 37, 1–23 (1977) (doi:10.1007/BF02727953)
-
Frank Wilczek, p. 959 of: Quantum Mechanics of Fractional-Spin Particles, Phys. Rev. Lett. 49 (1982) 957 (reprinted in Wilczek 1990, p. 166-168) doi:10.1103/PhysRevLett.49.957
Concretely, anyon-wavefunctions are identified with multi-valued functions on a configuration space of points, see there:
-
Tom Imbo, Chandni Shah Imbo, E. C. G. Sudarshan, Identical particles, exotic statistics and braid groups, Physics Letters B 234 1–2, (1990) 103-107 doi:10.1016/0370-2693(90)92010-G, pdf
-
Jürg Fröhlich, Fabrizio Gabbiani, Pieralberto Marchetti, around (1.1) in: Braid statistics in three-dimensional local quantum field theory, in: H.C. Lee (ed.) Physics, Geometry and Topology NATO ASI Series, 238 Springer (1990) doi:10.1007/978-1-4615-3802-8_2, pdf
-
J. Mund, Robert Schrader, Hilbert Spaces for Nonrelativistic and Relativistic “Free” Plektons (Particles with Braid Group Statistics), in Advances in dynamical systems and quantum physics (Capri, 1993), World Sci. (1995) 235–259 arXiv:hep-th/9310054v2
-
Garth A. Baker, Geoff S. Canright, Shashikant B. Mulay, Carl Sundberg, On the spectral problem for anyons, Communications in Mathematical Physics 153 (1993) 277–295 doi:10.1007/BF02096644
-
Gianfausto Dell’Antonio, Rodolfo Figari & Alessandro Teta, Statistics in Space Dimension Two, Letters in Mathematical Physics 40 (1997) 235–256 doi:10.1023/A:1007361832622
-
M.V.N. Murthy, Ramamurti Shankar, p. 7, 50Exclusion Statistics: From Pauli to Haldane (1999, 2009) dspace:123456789/334, pdf, pdf
Moreover, in quantum field theory one may formalize correlators as differential forms on configuration spaces of points. This perspective was originally considered specifically for Chern-Simons theory in:
- Scott Axelrod, Isadore Singer, Chern–Simons Perturbation Theory II, J. Diff. Geom. 39 (1994) 173-213 (arXiv:hep-th/9304087)
which was re-amplified in:
-
Raoul Bott, Alberto Cattaneo, Remark 3.6 in Integral invariants of 3-manifolds, J. Diff. Geom., 48 (1998) 91-133 (arXiv:dg-ga/9710001)
-
Alberto Cattaneo, Pavel Mnev, Remark 11 in Remarks on Chern-Simons invariants, Commun.Math.Phys.293:803-836,2010 (arXiv:0811.2045)
-
Alberto Cattaneo, Pavel Mnev, Nicolai Reshetikhin, appendix B of Perturbative quantum gauge theories on manifolds with boundary, Communications in Mathematical Physics, January 2018, Volume 357, Issue 2, pp 631–730 (arXiv:1507.01221, doi:10.1007/s00220-017-3031-6)
and highlighted as a means to obtain graph complex-models for the de Rham cohomology of configuration spaces of points in
-
Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)
-
Maxim Kontsevich, pages 11-12 of Feynman diagrams and low-dimensional topology, First European Congress of Mathematics, 1992, Paris, vol. II, Progress in Mathematics 120, Birkhäuser (1994), 97–121 (pdf)
with full details and proofs in
- Pascal Lambrechts, Ismar Volić, sections 6 and 7 of Formality of the little N-disks operad, Memoirs of the American Mathematical Society no. 1079, 2014 (arxiv:0808.0457, doi:10.1090/memo/1079)
see also
- Ricardo Campos, Najib Idrissi, Pascal Lambrechts, Thomas Willwacher, Configuration Spaces of Manifolds with Boundary (arXiv:1802.00716)
A systematic development of Euclidean perturbative quantum field theory with n-point functions considered as smooth functions on Fulton-MacPherson compactifications/wonderful compactifications of configuration spaces of points and more generally of subspace arrangements is due to
-
Christoph Bergbauer, Romeo Brunetti, Dirk Kreimer, Renormalization and resolution of singularities, ESI preprint 2010 (arXiv:0908.0633, ESI:2244)
-
Christoph Bergbauer, Renormalization and resolution of singularities, talks as IHES and Boston, 2009 (pdf)
-
Marko Berghoff, Wonderful renormalization, 2014 (pdf, doi:10.18452/17160)
-
Marko Berghoff, Wonderful compactifications in quantum field theory, Communications in Number Theory and Physics Volume 9 (2015) Number 3 (arXiv:1411.5583)
Analogous discussion for Hilbert schemes of points:
- Jian Zhou, K-Theory of Hilbert Schemes as a Formal Quantum Field Theory (arXiv:1803.06080)
Discussion specifically in topological quantum field theory with an eye towards supersymmetric field theory, in terms of the ordinary homology of configuration spaces of points:
- Christopher Beem, David Ben-Zvi, Mathew Bullimore, Tudor Dimofte, Andrew Neitzke, Secondary products in supersymmetric field theory, Ann. Henri Poincaré 21, 1235–1310 (2020). (arXiv:1809.00009, doi:10.1007/s00023-020-00888-3)
Braid representations via twisted cohomology of configuration spaces
The “hypergeometric integral” construction of conformal blocks for affine Lie algebra/WZW model-2d CFTs and of more general solutions to the Knizhnik-Zamolodchikov equation, via twisted de Rham cohomology of configuration spaces of points, originates with:
-
Vadim Schechtman, Alexander Varchenko, Integral representations of N-point conformal correlators in the WZW model, Max-Planck-Institut für Mathematik, (1989) Preprint MPI/89- cds:1044951
-
Etsuro Date, Michio Jimbo, Atsushi Matsuo, Tetsuji Miwa, Hypergeometric-type integrals and the -Knizhnik-Zamolodchikov equation, International Journal of Modern Physics B 04 05 (1990) 1049-1057 doi:10.1142/S0217979290000528
-
Atsushi Matsuo, An application of Aomoto-Gelfand hypergeometric functions to the Knizhnik-Zamolodchikov equation, Communications in Mathematical Physics 134 (1990) 65–77 doi:10.1007/BF02102089
-
Vadim Schechtman, Alexander Varchenko, Hypergeometric solutions of Knizhnik-Zamolodchikov equations, Lett. Math. Phys. 20 (1990) 279–283 doi:10.1007/BF00626523
-
Vadim Schechtman, Alexander Varchenko, Arrangements of hyperplanes and Lie algebra homology, Inventiones mathematicae 106 1 (1991) 139-194 dml:143938, pdf
following precursor observations due to:
-
Vladimir S. Dotsenko, Vladimir A. Fateev, Conformal algebra and multipoint correlation functions in 2D statistical models, Nuclear Physics B 240 3 (1984) 312-348 doi:10.1016/0550-3213(84)90269-4
-
Philippe Christe, Rainald Flume, The four-point correlations of all primary operators of the conformally invariant -model with Wess-Zumino term, Nuclear Physics B
282 (1987) 466-494 doi:10.1016/0550-3213(87)90693-6
The proof that for rational levels this construction indeed yields conformal blocks is due to:
-
Boris Feigin, Vadim Schechtman, Alexander Varchenko, On algebraic equations satisfied by correlators in Wess-Zumino-Witten models, Lett Math Phys 20 (1990) 291–297 doi:10.1007/BF00626525
-
Boris Feigin, Vadim Schechtman, Alexander Varchenko, On algebraic equations satisfied by hypergeometric correlators in WZW models. I, Commun. Math. Phys. 163 (1994) 173–184 doi:10.1007/BF02101739
-
Boris Feigin, Vadim Schechtman, Alexander Varchenko, On algebraic equations satisfied by hypergeometric correlators in WZW models. II, Comm. Math. Phys. 170 1 (1995) 219-247 [euclid:cmp/1104272957]
Review:
-
Alexander Varchenko, Multidimensional Hypergeometric Functions and Representation Theory of Lie Algebras and Quantum Groups, Advanced Series in Mathematical Physics 21, World Scientific 1995 (doi:10.1142/2467)
-
Ivan Cherednik, Section 8.2 of: Lectures on Knizhnik-Zamolodchikov equations and Hecke algebras, Mathematical Society of Japan Memoirs 1998 (1998) 1-96 doi:10.2969/msjmemoirs/00101C010
-
Pavel Etingof, Igor Frenkel, Alexander Kirillov, Lecture 7 in: Lectures on Representation Theory and Knizhnik-Zamolodchikov Equations, Mathematical surveys and monographs 58, American Mathematical Society (1998) ISBN:978-1-4704-1285-2, review pdf
-
Toshitake Kohno, Homological representations of braid groups and KZ connections, Journal of Singularities 5 (2012) 94-108 doi:10.5427/jsing.2012.5g, pdf
-
Toshitake Kohno, Local Systems on Configuration Spaces, KZ Connections and Conformal Blocks, Acta Math Vietnam 39 (2014) 575–598 doi:10.1007%2Fs40306-014-0088-6, pdf
-
Toshitake Kohno, Introduction to representation theory of braid groups, Peking 2018 pdf, pdf
(motivation from braid representations)
See also:
-
Alexander Varchenko, Asymptotic solutions to the Knizhnik-Zamolodchikov equation and crystal base, Comm. Math. Phys. 171 1 (1995) 99-137 arXiv:hep-th/9403102, doi:10.1007/BF02103772
-
Edward Frenkel, David Ben-Zvi, Section 14.3 in: Vertex Algebras and Algebraic Curves, Mathematical Surveys and Monographs 88, AMS 2004 ISBN:978-1-4704-1315-6, web
This “hypergeometric” construction uses results on the twisted de Rham cohomology of configuration spaces of points due to:
-
Peter Orlik, Louis Solomon, Combinatorics and topology of complements of hyperplanes, Invent Math 56 (1980) 167–189 doi:10.1007/BF01392549
-
Kazuhiko Aomoto, Gauss-Manin connection of integral of difference products, J. Math. Soc. Japan 39 2 (1987) 191-208 doi:10.2969/jmsj/03920191
-
Hélène Esnault, Vadim Schechtman, Eckart Viehweg, Cohomology of local systems on the complement of hyperplanes, Inventiones mathematicae 109.1 (1992) 557-561 pdf
-
Vadim Schechtman, H. Terao, Alexander Varchenko, Local systems over complements of hyperplanes and the Kac-Kazhdan conditions for singular vectors, Journal of Pure and Applied Algebra 100 1–3 (1995) 93-102 arXiv:hep-th/9411083, doi:10.1016/0022-4049(95)00014-N
also:
-
Peter Orlik, Hypergeometric integrals and arrangements, Journal of Computational and Applied Mathematics 105 (1999) 417–424 doi:10.1016/S0377-0427(99)00036-9, pdf
-
Daniel C. Cohen, Peter Orlik, Arrangements and local systems, Math. Res. Lett. 7 (2000) 299-316 arXiv:math/9907117, doi:10.4310/MRL.2000.v7.n3.a5
reviewed in:
- Yukihito Kawahara, The twisted de Rham cohomology for basic constructions of hyperplane arrangements and its applications, Hokkaido Math. J. 34 2 (2005) 489-505 doi:10.14492/hokmj/1285766233
Discussion for the special case of level (cf. at logarithmic CFT – Examples):
-
Fedor A. Smirnov, Remarks on deformed and undeformed Knizhnik-Zamolodchikov equations, arXiv:hep-th/9210051
-
Fedor A. Smirnov, Form factors, deformed Knizhnik-Zamolodchikov equations and finite-gap integration, Communications in Mathematical Physics 155 (1993) 459–487 doi:10.1007/BF02096723, arXiv:hep-th/9210052
-
S. Pakuliak, A. Perelomov, Relation Between Hyperelliptic Integrals, Mod. Phys. Lett. 9 19 (1994) 1791-1798 doi:10.1142/S0217732394001647
Interpretation of the hypergeometric construction as happening in twisted equivariant differential K-theory, showing that the K-theory classification of D-brane charge and the K-theory classification of topological phases of matter both reflect braid group representations as expected for defect branes and for anyons/topological order, respectively:
As moduli of Dp-D(p+4)-brane bound states:
Discussion of configuration spaces of possibly coincident points, hence of symmetric products as moduli spaces of D0-D4-brane bound states:
- Cumrun Vafa, Instantons on D-branes, Nucl. Phys. B463 (1996) 435-442 (arXiv:hep-th/9512078)
with emphasis to the resulting configuration spaces of points, as in
- Cumrun Vafa, Edward Witten, Section 4.1 of: A Strong Coupling Test of S-Duality, Nucl. Phys. B431:3-77, 1994 (arXiv:hep-th/9408074)
Last revised on May 10, 2025 at 07:31:39. See the history of this page for a list of all contributions to it.